北航惯性导航大作业任务.docx

北航惯性导航大作业任务.docx

《北航惯性导航大作业任务.docx》由会员分享，可在线阅读，更多相关《北航惯性导航大作业任务.docx（32页珍藏版）》请在冰豆网上搜索。

北航惯性导航大作业任务

惯性导航基础课程大作业报告

（一）

光纤陀螺误差建模与分析

班级：

111514

姓名：

学号

2014年5月26日

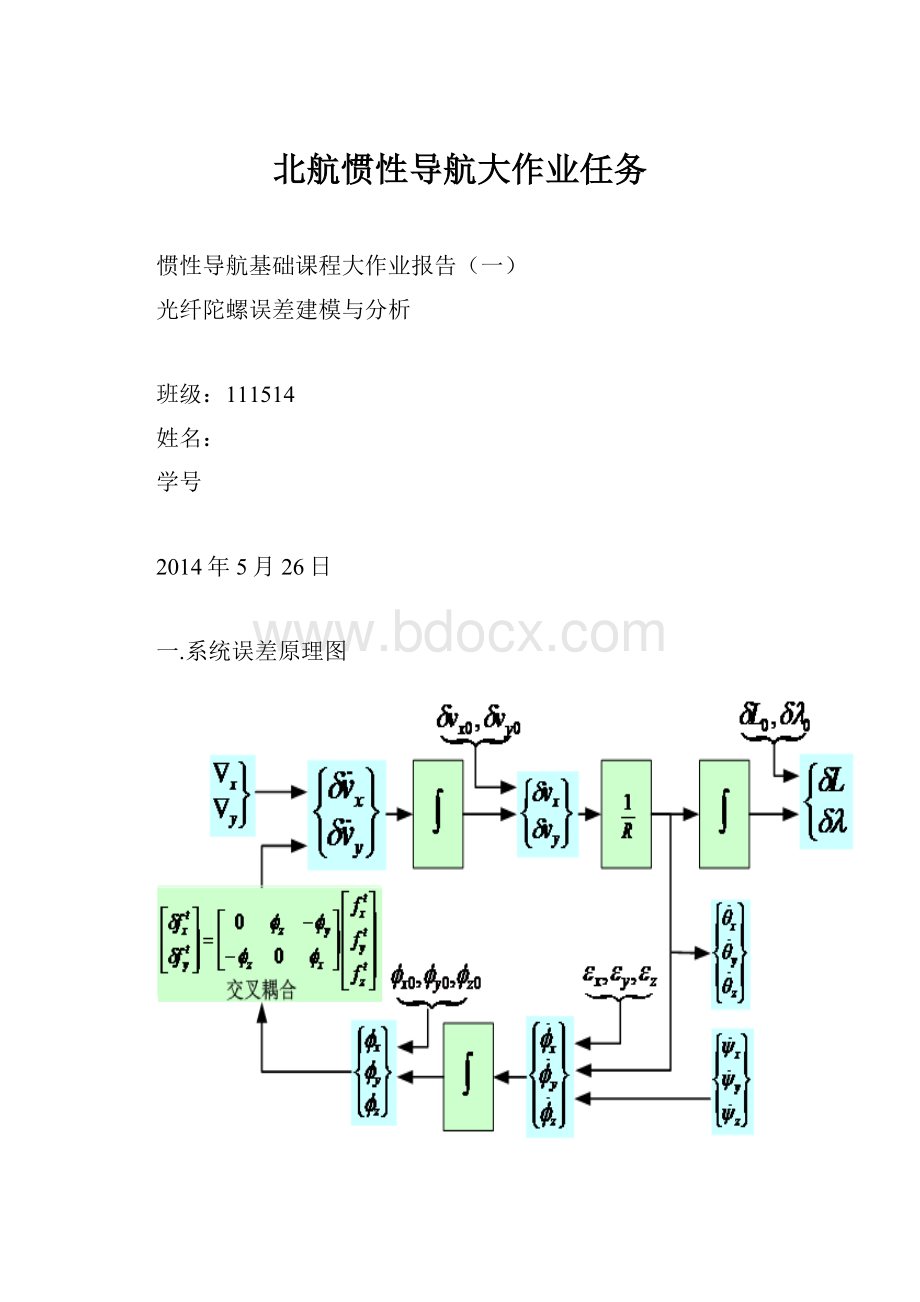
一.系统误差原理图

二.系统误差的分析

（一）漂移引起的系统误差

1.εx，εy，εz对东向速度误差δVx的影响

clc;clearall;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

e=0.1*180/pi;

mcVx1=e*g*sin（L）/（Ws^2-Wie^2）*（sin（Wie*t）-Wie*sin（Ws*t）/Ws）;

mcVx2=e*（（Ws^2-（Wie^2）*（（cos（L））^2））/（Ws^2-Wie^2）*cos（Ws*t）-（Ws^2）*（（sin（L））^2）*cos（Wie*t）/（Ws^2-Wie^2）-（cos（L））^2）;

mcVx3=（sin（L））*（cos（L））*R*e*（（Ws^2）*cos（Wie*t）/（Ws^2-Wie^2）-（Wie^2）*cos（Ws*t）/（Ws^2-Wie^2）-1）;

plot（t,[mcVx1',mcVx2',mcVx3']）;

title（'Ex,Ey,Ez对Vx的影响'）;

xlabel（'时间t'）;

ylabel（'Vx（t）'）;

legend（'Ex-mcVx1','Ey-mcVx2','Ez-mcVx3'）;

grid;

axissquare;

分析：

εx，εy，εz对东向速度误差δVx均有地球自转周期的影响，εx，εy还会有舒勒周期分量的影响，其中，εy对δVx的影响较大。

2.εx，εy，εz对东向速度误差δVy的影响

clc;clearall;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

e=0.1*180/pi;

mcVy1=e*g*（cos（Wie*t）-cos（Ws*t））/（Ws^2-Wie^2）;

mcVy2=g*sin（L）*e/（Ws^2-Wie^2）*（sin（Wie*t）-Wie/Ws*sin（Ws*t））;

mcVy3=g*cos（L）*e/（Ws^2-Wie^2）*（sin（Wie*t）-Wie/Ws*sin（Ws*t））;

plot（t,[mcVy1',mcVy2',mcVy3']）;

title（'Ex,Ey,Ez对Vy的影响'）;

xlabel（'时间t'）;

ylabel（'Vy（t）'）;

legend（'Ex-mcVy1','Ey-mcVy2','Ez-mcVy3'）;

grid;

axissquare;

分析：

εx，εy，εz对北向速度误差δVy均有地球自转周期，舒勒周期分量的影响。

其中，εx对δVy的影响较大;εy，εz产生的影响几乎相近。

3.εx，εy，εz对东向速度误差δL的影响

clc;clearall;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

mcL1=Ws^2*0.1/a*（d/Wie-f/Ws）;

mcL2=（Ws^2*Wie*b/a*（h/Ws^2-e/Wie^2）+b/Wie）*0.1;

mcL3=（Ws^2*c*e/Wie/a-Wie*c*h/a-c/Wie）*0.1;

plot（t,[mcL1',mcL2',mcL3']）;

title（'Ex,Ey,Ez对mcL的影响'）;

xlabel（'时间t'）;

ylabel（'mcL（t）'）;

legend（'Ex-mcL1','Ey-mcL2','Ez-mcL3'）;

grid;

分析：

εx，εy，εz对纬度误差δL均有地球自转周期的影响，εx还会有舒勒周期分量的影响。

4.εx，εy，εz对东向速度误差δλ的影响

clc;clearall;

t=1:

0.01:

50;

pi=3.14;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

mcLONG1=（tan（L）/Wie*（1-e）-Wie*c*h/a）*0.1;

mcLONG2=（sec（L）*（Ws^2-Wie^2*c^2）*f/Ws/a-Ws^2*tan（L）*b*d/Wie/a-t*c）*0.1;

mcLONG3=（Ws^2*b*d/Wie/a-Wie^2*b*f/a/Ws-t*b）*0.1;

plot（t,[mcLONG1',mcLONG2',mcLONG3']）;

title（'Ex,Ey,Ez对mcLONG.的影响'）;

xlabel（'时间t'）;

ylabel（'mcLONG.（t）'）;

legend（'Ex-mcLONG.1','Ey-mcLONG.2','Ez-mcLONG.3'）;

grid;

axissquare;

分析：

εx，εy，εz对经度误差δλ均有地球自转周期的影响，εy还会有舒勒周期分量的影响，其中，εy，εz还产生了随时间累积的分量。

5.εx，εy，εz对东向速度误差δφX的影响

clc;clearall;

t=1:

0.01:

25;

pi=3.14;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

mcAngle1=（Ws*f-Wie*d）/a*0.1;

mcAngle2=Wie*b*（e-h）/a*0.1;

mcAngle3=Wie*c*（h-e）/a*0.1;

plot（t,[mcAngle1',mcAngle2',mcAngle3']）;

title（'Ex,Ey,Ez对mcAngle的影响'）;

xlabel（'时间t'）;

ylabel（'mcAngle（t）'）;

legend（'Ex-mcAngle1','Ey-mcAngle2','Ez-mcAngle3'）;

grid;

axissquare;

分析：

εx，εy，εz对水平方位误差φx均有地球自转周期，舒勒周期分量的影响，其中，εx对φx产生的影响最大。

5.εx，εy，εz对东向速度误差δφY的影响

clc;clearall;

t=1:

0.01:

25;

pi=3.14;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

mcAngle1=Wie*b*（h-e）/a*0.1;

mcAngle2=（（Ws^2-Wie^2*c^2）/Ws/a*f-Wie*b^2/a*d）*0.1;

mcAngle3=Wie*b*c/a*（d-Wie/Ws*f）*0.1;

plot（t,[mcAngle1',mcAngle2',mcAngle3']）;

title（'Ex,Ey,Ez对mcAngley的影响'）;

xlabel（'时间t'）;

ylabel（'mcAngley（t）'）;

legend（'Ex-mcAngle1','Ey-mcAngle2','Ez-mcAngle3'）;

grid;

axissquare;

分析：

εx，εy，εz对水平方位误差φy均有地球自转周期的影响，而εx，εy还产生了舒勒周期分量的影响，其中，εy对φy产生的影响最大。

5.εx，εy，εz对东向速度误差δφZ的影响

clc;clearall;

t=1:

0.01:

25;

pi=3.14;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

mcAngle1=（sec（L）/Wie*（1-e）+Wie*b*b/c*（h-e）/a）*0.1;

mcAngle2=（Wie^2*b*c-Ws^2*b/c）/a*（d/Wie-f/Ws）*0.1;

mcAngle3=（（Ws^2-Wie^2*c^2）*d/Wie/a-Wie^2*b^2*f/Ws/a）*0.1;

plot（t,[mcAngle1',mcAngle2',mcAngle3']）;

title（'Ex,Ey,Ez对mcAnglez的影响'）;

xlabel（'时间t'）;

ylabel（'mcAnglez（t）'）;

legend（'Ex-mcAngle1','Ey-mcAngle2','Ez-mcAngle3'）;

grid;

分析：

εx，εy，εz对方位姿态误差φz均有地球自转周期的影响，而εy还产生了舒勒周期分量的影响，其中，εx对φz产生的影响最大。

（二）加速度计零偏引起的系统误差

1.Δx对φy,φz以及Δy对φx的影响

clc;clearall;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

amc=0.0001*g;

mcAnglez=b/c/g*（1-h）*amc*180/pi*3600;

mcAngley=（1-h）/g*amc*180/pi*3600;

mcAnglex=-（1-h）/g*amc*180/pi*3600;

subplot（311）;plot（t,mcAnglex,'r-'）;xlabel（'时间t'）;ylabel（'mcAnglex（t）'）;

legend（'amcy-mcAnglex'）;grid;

subplot（312）;plot（t,mcAngley,'g-'）;xlabel（'时间t'）;ylabel（'mcAngley（t）'）;

legend（'amcx-mcAngley'）;grid;

subplot（313）;plot（t,mcAnglez,'b-'）;xlabel（'时间t'）;ylabel（'mcAnglez（t）'）;

legend（'amcx-mcAnglez'）;grid;

分析：

Δx对φy,φz以及Δy对φx的影响包含了常值分量和舒乐振荡分量。

2.Δx对δVx,Δy对δVy,Δy对δL,Δx对δλ的影响

clc;clearall;

t=1:

0.01:

25;

pi=3.14;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=Ws^2-Wie^2;

b=sin（L）;

c=cos（L）;

d=sin（Wie*t）;

e=cos（Wie*t）;

f=sin（Ws*t）;

h=cos（Ws*t）;

amc=0.0001*g;

mcVx=f/Ws*amc;

mcVy=f/Ws*amc;

mcL=（1-h）/g*amc*180/pi*3600;

mcLONG=sec（L）*amc/g*（1-h）*180/pi*3600;

subplot（221）;plot（t,mcVx,'r:

'）;xlabel（'时间t'）;ylabel（'mcVx（t）'）;grid;

subplot（222）;plot（t,mcVy,'g:

'）;xlabel（'时间t'）;ylabel（'mcVy（t）'）;grid;

subplot（223）;plot（t,mcL,'b:

'）;xlabel（'时间t'）;ylabel（'mcL（t）'）;grid;

subplot（224）;plot（t,mcLONG,'b:

'）;xlabel（'时间t'）;ylabel（'mcLONG（t）'）;grid;

分析：

Δx对δVx,Δy对δVy,Δy对δL,Δx对δλ,均包含了常值分量和舒乐振荡分量的影响。

（三）起始误差对系统误差的影响

1.δVx0,δVy0,δL0,φx0,φy0,φz0对δVx的影响

symss;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=s^2+Ws^2;

b=s^2+Wie^2;

c=sin（L）;

d=cos（L）;

c11=s/a;

c12=0;

c13=s*g*Wie*c/a/b;

c14=c13;

c15=-g*（s^2+Wie^2*d^2）/a/b;

c16=-g*Wie^2*c*d/a/b;

mcVx1=ilaplace（c11*0.1）;

mcVx3=ilaplace（c13*0.0005*pi/180）;

mcVx4=ilaplace（c14*20/3600*pi/180）;

mcVx5=ilaplace（c15*20/3600*pi/180）;

mcVx6=ilaplace（c16*5/60*pi/180）;

mcVx1t=subs（mcVx1）;

mcVx3t=subs（mcVx3）;

mcVx4t=subs（mcVx4）;

mcVx5t=subs（mcVx5）;

mcVx6t=subs（mcVx6）;

plot（t,mcVx1t）;title（'mcVx0对mcVx的影响'）;xlabel（'时间t'）;ylabel（'mcVx（t）'）;grid;

figure

（2）;

plot（t,mcVx3t）;title（'mcL0对mcVx的影响'）;xlabel（'时间t'）;ylabel（'mcVx（t）'）;grid;

figure（3）;

plot（t,mcVx4t,'g*',t,mcVx5t,'g+',t,mcVx6t,'g-'）;

legend（'anglex0-mcVx','angley0-mcVx','anglez0-mcVx'）;

title（'初始水平姿态角，方位姿态角对mcVx的影响'）;xlabel（'时间t'）;ylabel（'mcVx（t）'）;grid;

分析：

δVx0对δVx只有舒乐周期震荡的影响；δL0对δVx有地球自转周期和舒乐周期震荡两个方面的影响；φx0,φy0,φz0对δVx有地球自转周期和舒乐振荡周期的影响，且φy0产生的影响最大。

2.δVx0,δVy0,δL0,φx0,φy0,φz0对δVy的影响

symss;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=s^2+Ws^2;

b=s^2+Wie^2;

c=sin（L）;

d=cos（L）;

c21=0;

c22=s/a;

c23=-g*Wie^2/a/b;

c24=s^2*g/a/b;

c25=s*g*Wie*c/a/b;

c26=-s*g*Wie*d/a/b;

mcVy2=ilaplace（c22*0.1）;

mcVy3=ilaplace（c23*0.0005*pi/180）;

mcVy4=ilaplace（c24*20/3600*pi/180）;

mcVy5=ilaplace（c25*20/3600*pi/180）;

mcVy6=ilaplace（c26*5/60*pi/180）;

mcVy1t=subs（mcVy1）;

mcVy3t=subs（mcVy3）;

mcVy4t=subs（mcVy4）;

mcVy5t=subs（mcVy5）;

mcVy6t=subs（mcVy6）;

plot（t,mcVy1t）;title（'mcVy0对mcVy的影响'）;xlabel（'时间t'）;ylabel（'mcVy（t）'）;grid;

figure

（2）;

plot（t,mcVy3t）;title（'mcL0对mcVy的影响'）;xlabel（'时间t'）;ylabel（'mcVy（t）'）;grid;

figure（3）;

plot（t,mcVy4t,'.',t,mcVy5t,'+',t,mcVy6t,'-'）;

legend（'anglex0-mcVy','angley0-mcVy','anglez0-mcVy'）;

title（'初始水平姿态角，方位姿态角对mcVy的影响'）;xlabel（'时间t'）;ylabel（'mcVy（t）'）;grid;

分析：

δVy0对δVy只有舒乐周期震荡的影响；δL0对δVy有地球自转周期和舒乐周期震荡两个方面的影响；φx0,φy0,φz0对δVy有地球自转周期和舒乐振荡周期的影响，且φx0,φz0产生的影响较大。

3.δVx0,δVy0,δL0,φx0,φy0,φz0对δL0的影响

symss;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=s^2+Ws^2;

b=s^2+Wie^2;

c=sin（L）;

d=cos（L）;

c31=0;

c32=1/a/R;

c33=s/a;

c34=s*Ws^2/a/b;

c35=Ws^2*Wie*c/a/b;

c36=-Ws^2*Wie*d/a/b;

mcL2=ilaplace（c32*0.1）;

mcL3=ilaplace（c33*0.0005）;

mcL4=ilaplace（c34*20/3600）;

mcL5=ilaplace（c35*20/3600）;

mcL6=ilaplace（c36*5/60）;

mcL2t=subs（mcL2）;

mcL3t=subs（mcL3）;

mcL4t=subs（mcL4）;

mcL5t=subs（mcL5）;

mcL6t=subs（mcL6）;

plot（t,mcL2t）;title（'mcVy0对mcL的影响'）;xlabel（'时间t'）;ylabel（'mcL（t）'）;grid;

figure

（2）;

plot（t,mcVy3t）;title（'mcL0对mcL的影响'）;xlabel（'时间t'）;ylabel（'mcL（t）'）;grid;

figure（3）;

plot（t,mcL4t,'.',t,mcL5t,'+',t,mcL6t,'-'）;

legend（'angleX0-mcL','angley0-mcL','anglez0-mcL'）;

title（'初始水平姿态角，方位姿态角对mcL的影响'）;xlabel（'时间t'）;ylabel（'mcL（t）'）;grid;

分析：

δVy0对δL只有舒乐周期震荡的影响；δL0对δL有地球自转周期和舒乐周期震荡两个方面的影响；φx0,φy0,φz0对δL有地球自转周期和舒乐振荡周期的影响，且φz0产生的影响较大。

4.δVx0,δVy0,δL0,φx0,φy0,φz0对φx的影响

symss;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=s^2+Ws^2;

b=s^2+Wie^2;

c=sin（L）;

d=cos（L）;

c41=0;

c42=-1/a/R;

c43=-s*Wie^2/a/b;

c44=s^3/a/b;

c45=s^2*Wie*c/a/b;

c46=-s^2*Wie*d/a/b;

anglex2=ilaplace（c42*0.1）;

anglex3=ilaplace（c43*0.0005）;

anglex4=ilaplace（c44*20/3600）;

anglex5=ilaplace（c45*20/3600）;

anglex6=ilaplace（c46*5/60）;

anglex2t=subs（anglex2）;

anglex3t=subs（anglex3）;

anglex4t=subs（anglex4）;

anglex5t=subs（anglex5）;

anglex6t=subs（anglex6）;

plot（t,anglex2t）;title（'mcVy0对abglex的影响'）;xlabel（'时间t'）;ylabel（'abglex'）;grid;

figure

（2）;

plot（t,anglex3t）;title（'mcL0对anglex的影响'）;xlabel（'时间t'）;ylabel（'anglex'）;grid;

figure（3）;

plot（t,anglex4t,'.',t,anglex5t,'+',t,anglex6t,'-'）;

legend（'angleX0-anglex','angley0-anglex','anglez0-anglex'）;

title（'初始水平姿态角，方位姿态角对anglex的影响'）;xlabel（'时间t'）;ylabel（'anglex'）;grid;

分析：

δVy0对φx只有舒乐周期震荡的影响；δL0对φx有地球自转周期和舒乐周期震荡两个方面的影响；φx0,φy0,φz0对φx有地球自转周期和舒乐振荡周期的影响，且φx0,φz0产生的影响较大。

5.δVx0,δVy0,δL0,φx0,φy0,φz0对φy的影响

clc;clearall;

symss;

t=1:

0.01:

25;

g=9.8;

L=pi/180*39;

Ws=2*pi/84.4*60;

Wie=2*pi/24;

R=g/（Ws）^2;

a=s^2+Ws^2;

b=s^2+Wie^2;

c=sin（L）;

d=cos（L）;

c51=1/R/a;

c52=0;

c53=-s^2*Wie*c/a/b;

c54=-s*Wie*c/a/b;

c55=s*（Wie^2*c*d）/a/b;

c56=s*Wie^2*c*d/a/b;

angley1=ilaplace（c51*0.1）