七年级下册第五章相交线与平行线导学案.docx

七年级下册第五章相交线与平行线导学案.docx

《七年级下册第五章相交线与平行线导学案.docx》由会员分享，可在线阅读，更多相关《七年级下册第五章相交线与平行线导学案.docx（21页珍藏版）》请在冰豆网上搜索。

七年级下册第五章相交线与平行线导学案

第五章相交线与平行线导学案

01相交线

练习一：

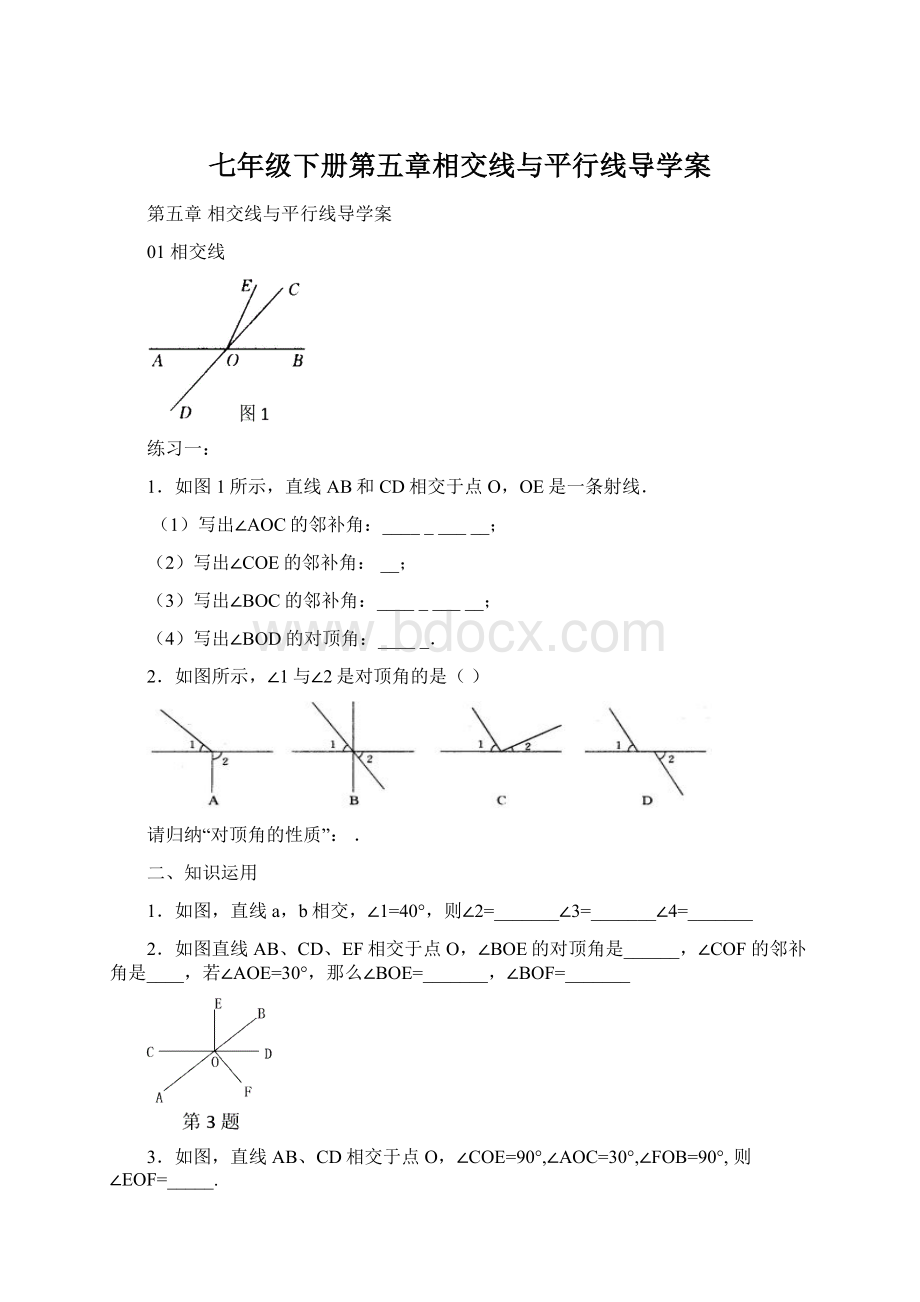
1．如图1所示，直线AB和CD相交于点O，OE是一条射线．

（1）写出∠AOC的邻补角：

__________；

（2）写出∠COE的邻补角：

__；

（3）写出∠BOC的邻补角：

__________；

（4）写出∠BOD的对顶角：

_____．

2．如图所示，∠1与∠2是对顶角的是（）

请归纳“对顶角的性质”：

．

二、知识运用

1．如图，直线a，b相交，∠1=40°，则∠2=_______∠3=_______∠4=_______

2．如图直线AB、CD、EF相交于点O，∠BOE的对顶角是______，∠COF的邻补角是____，若∠AOE=30°，那么∠BOE=_______，∠BOF=_______

3．如图，直线AB、CD相交于点O，∠COE=90°,∠AOC=30°,∠FOB=90°,则∠EOF=_____.

三、知识提高

1．若两个角互为邻补角，则它们的角平分线所夹的角为度．

2．如图所示，直线a，b，c两两相交，∠1=60°，∠2=

∠4，求∠3、∠5的度数．

02垂线

如图：

用几何语言表示：

方式⑴∵∠AOC=90°∴AB_____CD，垂足是_____

方式⑵∵AB⊥CD于O∴∠AOC=______

探索一：

请你认真画一画，看看有什么收获．

⑴如图1，利用三角尺或量角器画已知直线

的垂线，这样的垂线能画__________条；

⑵如图2，经过直线

上一点A画

的垂线，这样的垂线能画_____条；

⑶如图3，经过直线

外一点B画

的垂线，这样的垂线能画_____条；

（图1）（图2）（图3a）（图3b）

经过探索发现：

在同一平面内，过一点有且只有_____条直线与已知直线垂直．

二、知识运用

1．如图所示，OA⊥OB，OC是一条射线，若∠AOC=120°，

求∠BOC度数

2．如图所示，直线AB，CD相交于点O，P是CD上一点．

（1）过点P画AB的垂线PE，垂足为E．

（2）过点P画CD的垂线，与AB相交于F点．

（3）比较线段PE，PF，PO三者的大小关系

简单说成：

．还有，直线外一点到这条直线的垂线段的叫做点到直线的距离.注意：

垂线是，垂线段是一条，点到直线的距离是一个数量，不能说“垂线段”是距离.

三、知识提高

1．在下列语句中，正确的是（）．

A．在同一平面内，一条直线只有一条垂线

B．在同一平面内，过直线上一点的直线只有一条

C．在同一平面内，过直线上一点且垂直于这条直线的直线有且只有一条

D．在同一平面内，垂线段就是点到直线的距离

2．如图所示，AC⊥BC，CD⊥AB于D，AC=5cm，BC=12cm，AB=13cm，则点B到AC的距离是________，点A到BC的距离是_______，点C到AB的距离是_______，AC>CD的依据是_________．

03同位角、内错角、同旁内角

探索：

如图，直线c分别与直线a、b相交（也可以说两条

直线a、b被第三条直线c所截），得到8个角，通常称为

“三线八角”，那么这8个角之间有哪些关系呢？

观察填表：

表一

位置1

位置2

结论

∠1和∠5

处于直线c的同侧

处于直线a、b的同一方

这样位置的一对角就称为同位角

∠2和∠8

处于直线c的（）侧

这样位置的一对角就称为（）

∠3和∠6

处于直线a、b的（）方

这样位置的一对角就称为（）

∠1和∠5

这样位置的一对角就称为（）

表二

位置1

位置2

结论

∠4和∠8

处于直线c的两侧

处于直线a、b之间

这样位置的一对角就称为内错角

∠3和∠5

这样位置的一对角就称为（）

表三

位置1

位置2

结论

∠3和∠8

处于直线c的（）侧

处于直线a、b（）

这样位置的一对角就称为同旁内角

∠4和∠5

这样位置的一对角就称为（）

二、知识运用

1．如图1所示，∠1与∠2是___角，∠2与∠4是_角，∠2与∠3是___角．

（图1）（图2）（图3）

2．如图2所示，∠1与∠2是____角，是直线______和直线_______被直线_______所截而形成的，∠1与∠3是_____角，是直线________和直线______被直线________所截而形成的．

三、知识提高

．如图，直线DE、BC被直线AB所截.

⑴∠1与∠2、∠1与∠3、∠1与∠4各是什么角？

⑵如果∠1=∠4，那么∠1和∠2相等吗？

∠1和∠3互补吗？

为什么？

05平行线

练习一：

1．下列说法中，正确的是（）．

A．两直线不相交则平行B．两直线不平行则相交

C．若两线段平行，那么它们不相交D．两条线段不相交，那么它们平行

2．在同一平面内，有三条直线，其中只有两条是平行的，那么交点有（）．

A．0个B．1个C．2个D．3个

（平行公理）：

经过直线外一点，一条直线与这条直线平行.

（平行线的传递性）：

如果两条直线都与第三条直线平行，那么这两条直线也互相平行.简单的说就是：

平行于同一直线的两直线平行.

用几何语言可表示为：

如果

∥

，

∥

，那么.

二、知识运用

1．如图1所示，与AB平行的棱有_______条，与AA′平行的棱有_____条．

2．如图2所示，按要求画平行线．

（1）过P点画AB的平行线EF；

（2）过P点画CD的平行线MN．

3．如图3所示，点A，B分别在直线

，

上，

（1）过点A画到

的垂线段；

（2）过点B画直线

∥

．

（图1）（图2）（图3）

三、知识提高

1．下列说法中，错误的有（）．

①若a与c相交，b与c相交，则a与b相交;

②若a∥b，b∥c，那么a∥c;

③过一点有且只有一条直线与已知直线平行;

④在同一平面内，两条直线的位置关系有平行、相交、垂线三种

A．3个B．2个C．1个D．0个

2．判断题

（1）不相交的两条直线叫做平行线.（）

（2）在同一平面内，不相交的两条射线是平行线.（）

（3）如果一条直线与两条平行线中的一条平行,那么它与另一条也互相平行.（）

06平行线的判定

一、知识梳理

如图，将下列空白补充完整（填1种就可以）

判定方法1（判定公理）

几何语言表述为：

∵∠___=∠___∴AB∥CD

由判定方法1，结合对顶角的性质，我们可以得到：

判定方法2（判定定理）

几何语言表述为：

∵∠___=∠___∴AB∥CD

由判定方法1，结合邻补角的性质，我们可以得到：

判定方法3（判定定理）

几何语言表述为：

∵∠___+∠___=180°∴AB∥CD

二、知识运用

（1题）（2题）

1．如图1所示，若∠1=∠2，则_____∥______，根据是______．

若∠1=∠3，则______∥______，根据是_________．

2．如图2所示，若∠1=62°，∠2=118°，则_____∥_____，根据是________

3．根据图3完成下列填空（括号内填写定理或公理）

（1）∵∠1=∠4（已知）

∴　　　∥　　　（）

（2）∵∠ABC+∠=180°（已知）

（图3）

∴AB∥CD（）

（3）∵∠=∠（已知）

∴AD∥BC（）

（4）∵∠5=∠（已知）

∴AB∥CD（）

如图4，几何语言表述为：

∵

⊥

，

⊥

∴

三、知识提高

（图4）

1．如图所示，AB⊥BC，BC⊥CD，BF和CE是射线，并且∠1=∠2，

试说明BF∥CE．

07平行线的性质

一、知识梳理

平行线的性质，如图5，将下列空白补充完整（填1种就可以）

性质1（性质公理）

几何语言表述为：

∵AB∥CD∴∠___=∠___

由性质1，结合对顶角的性质，我们可以得到：

（图5）

性质2（性质定理）

几何语言表述为：

∵AB∥CD∴∠___=∠___

由性质1，结合邻补角的性质，我们可以得到：

性质3（性质定理）

几何语言表述为：

∵AB∥CD∴∠___+∠___=

二、知识运用

1.根据右图6将下列几何语言补充完整

（图6）

（1）∵AD∥（已知）

∴∠A+∠ABC=180°（）

（2）∵AB∥（已知）

∴∠4=∠（）

∠ABC=∠（）

（图7）

2.如右图7所示，BE平分∠ABC，DE∥BC，图中相等的角共有（）

A.3对B.4对C.5对D.6对

3、如图8，AB∥CD,∠1=45°,∠D=∠C,求∠D、∠C、∠B的度数.

（图8）

探索二：

用三角尺和直尺画平行线，做成一张5×5个格子的方格纸.观察做出的方格纸的一部分（如图），线段

、

、…、

都与两条平行的横线

和

垂直吗？

它们的长度相等吗？

像这样，同时垂直于两条平行直线，并且夹在这两条平行线间的线段的长度相等，叫做这两条平行线间的距离，即平行线间的距离处处相等.

三、知识提高

1．如图所示，已知直线AB∥CD，且被直线EF所截，若∠1=50°，则∠2=____，∠3=______．

2．如图所示，AB∥CD，AF交CD于E，若∠CEF=60°，则∠A=______．

3．如图所示，已知AB∥CD，BC∥DE，∠1=120°，则∠2=______．

（1题）（2题）（3题）

08平行线的判定及性质习题课

一.练习：

1．如图1，若∠1=∠2，那么_____∥______，根据_____．

若a∥b，那么∠3=_____，根据_____．

（图1）（图2）（图3）（图4）

2．如图2，∵∠1=∠2，∴_______∥_______，根据________．

∴∠B=______，根据________．

3．如图3，若AB∥CD，那么________=_______；若∠1=∠2，那么_____∥_____；

若BC∥AD，那么_______=_______；若∠A+∠ABC=180°，那么______∥_____

4．如图4，一条公路两次拐弯后，和原来的方向相同，如果第一次拐的角是136°（即∠ABC），那么第二次拐的角（∠BCD）是度，根据___．

5．如右图，修高速公路需要开山洞，为节省时间，要在山两面A，B

同时开工，在A处测得洞的走向是北偏东76°12′，那么在B处

应按什么方向开口，才能使山洞准确接通，请说明其中的道理．

6．如右图所示，潜望镜中的两个镜子是互相平行放置的，光线经过

E

镜子反射∠1=∠2，∠3=∠4，请你解释为什么开始进入潜望镜的光

线AE和最后离开潜望镜的光线DF是平行的．

F

二、知识提高

1．已知如图1，用一吸管吸吮易拉罐内的饮料时，吸管与易拉罐上部夹角∠1=74°，那么吸管与易拉罐下部夹角∠2=_______．

2．已知如图2，边OA，OB均为平面反光镜，∠AOB=40°，在OB上有一点P，从P点射出一束光线经OA上的Q点反射后，反射光线QR恰好与OB平行，则∠QPB的度数是（）．