放大器极零点与频率响应.docx

放大器极零点与频率响应.docx

《放大器极零点与频率响应.docx》由会员分享，可在线阅读，更多相关《放大器极零点与频率响应.docx（28页珍藏版）》请在冰豆网上搜索。

放大器极零点与频率响应

关于放大器极、零点与频率响应的初步实验

1．极零点的复杂性与必要性

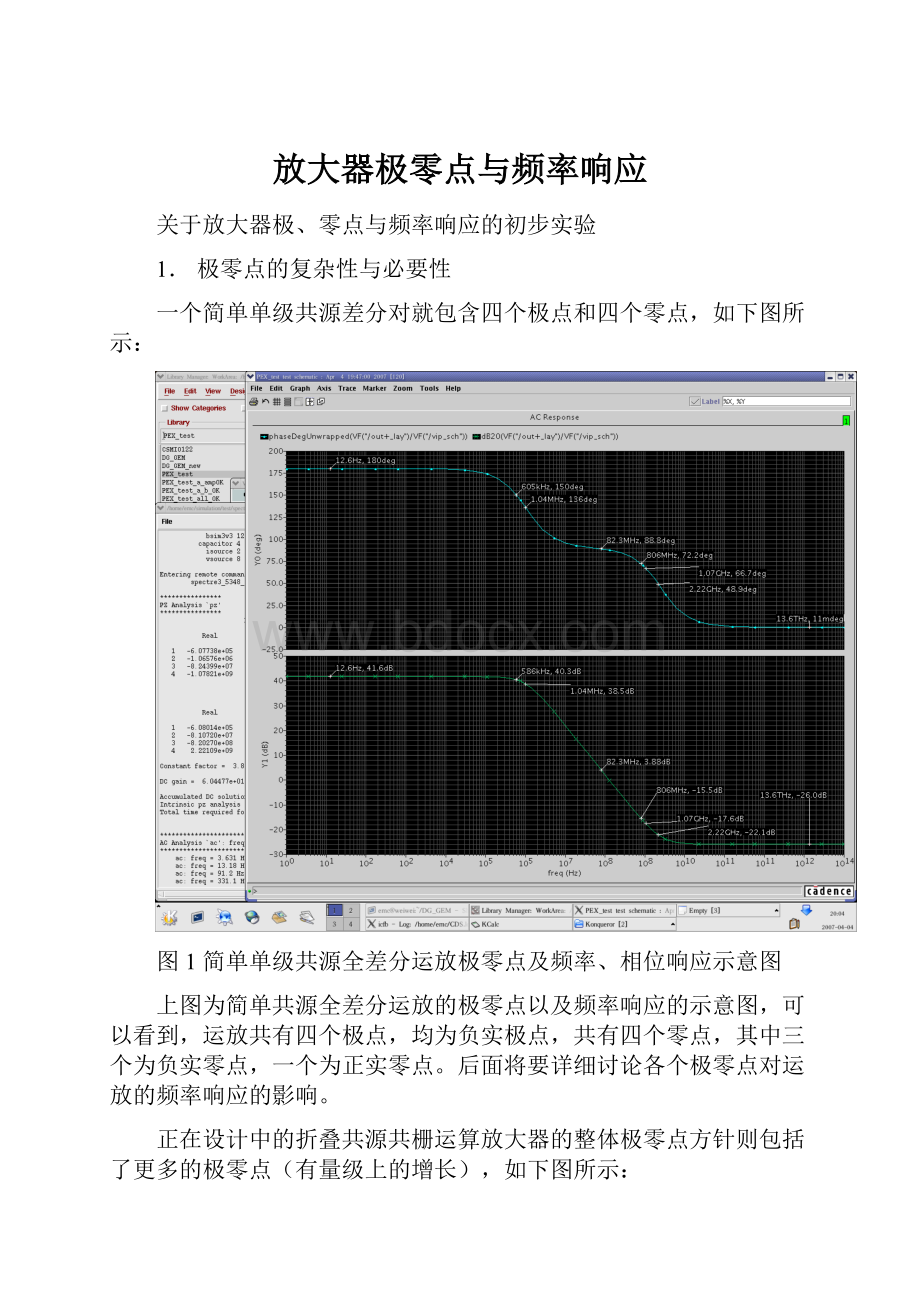
一个简单单级共源差分对就包含四个极点和四个零点，如下图所示：

图1简单单级共源全差分运放极零点及频率、相位响应示意图

上图为简单共源全差分运放的极零点以及频率响应的示意图，可以看到，运放共有四个极点，均为负实极点，共有四个零点，其中三个为负实零点，一个为正实零点。

后面将要详细讨论各个极零点对运放的频率响应的影响。

正在设计中的折叠共源共栅运算放大器的整体极零点方针则包括了更多的极零点（有量级上的增长），如下图所示：

图2folded-cascodewithgain-boostingandbandgapall-polesdetails

图3folded-cascodewithgain-boostingandbandgapall-zerosdetails

从上述两张图可以看到，面对这样数量的极零点数量（各有46个），精确的计算是不可能的，只能依靠计算机仿真。

但是手算可以估计几个主要极零点的大致位置，从而预期放大器的频率特性。

同时从以上图中也可以看到，详细分析极零点情况也是很有必要的。

可以看到46个极点中基本都为左半平面极点（负极点）而仿真器特别标出有一个正极点（RHP）。

由于一般放大器的极点均应为LHP，于是可以预期这个右半平面极点可能是一个设计上的缺陷所在。

（具体原因现在还不明，可能存在问题的方面：

1。

推测是主放大器的CMFB的补偿或者频率响应不合适。

2。

推测是两个辅助放大器的带宽或频率响应或补偿电容值不合适）其次可以从极零点的对应中看到存在众多的极零点对（一般是由电流镜产生），这些极零点对产生极零相消效应，减少了所需要考虑的极零点的个数。

另外可以看到46个零点中45个为负零点，一个为正零点，这个正零点即是需要考虑的对放大器稳定性产生直接影响的零点。

以上只是根据仿真结果进行的一些粗略的分析，进一步的学习和研究还需要进行一系列实验。

1．单极点传输函数——RC低通电路

首先看一个最简单的单极点系统——RC低通电路，其中阻值为1k，电容为1p，传输函数为：

则预计极点p0=1/（2πRC）=1.592e8Hz，仿真得到结果与此相同。

而从输出点的频率响应图中可以得到以下几个结论：

图4一阶RC积分电路

1）-3dB带宽点（截止频率）就是传输函数极点，此极点对应相位约为-45°。

2）相位响应从0°移向高频时的90°，即单极点产生+90°相移。

3）在高于极点频率时，幅度响应呈现-20dB/十倍频程的特性。

图5一阶RC电路极点与频率响应（R=1kC=1p）

2．单极点单零点系统——CR高通电路

简单的一阶CR电路，阻值/容值不变，传输函数为

预计系统存在单极点p0=1/2πRC，单零点z0=0，仿真得到单极点1.592e8Hz，单零点8.835e-6Hz，极点位置同RC电路，零点位置可以理解为一个无限趋近于零的值。

从频率响应曲线中同样有以下结论：

图6一阶CR电路

图7一阶CR电路幅频、相频响应（C=1pR=1k）

1）频率为0Hz（零点）时幅度为0（换算为dB时为负无穷大，故零点只能用一个ε小数表示），-3dB带宽（下截频）即为极点所在，对应相位45°。

2）相位响应从90°移向高频时的0°，即单极单零系统产生-90°相移。

（可以这样理解，零点使系统已经从极低频的180°相移并稳定到90°，然后单极点最终产生-90°相移，使相位最终稳定在0°）

3）零点频率之上，极点频率之下，幅度响应为+20dB/十倍频，极点频率之上为0dB。

结合单极点系统-20dB/十倍频的幅度响应特性可知，零点产生+20dB/十倍频的特性，并且极零点对幅度响应的影响可以叠加。

（证明：

极低频时，极点不起作用，即1>>sRC

从而

于是|Av|=20dB*lg（s）+C（即低频时为+20dB/十倍频）

高频时，sRC>>1，从而

，于是|Av|=0。

）

3．两阶RC系统

以上看到的一阶RC/CR电路均为最简单的非线性系统。

R和C的任意组合将可能产生极为复杂的系统，分析其传输函数将是一个求解高阶线性方程组的过程，使得精确的手算分析基本不可能。

但是对于实际应用的单极或多极放大器来说，其RC拓扑结构有其特殊性，一般都是π形电容结构，如下图：

这相当于一个两级放大器的电容电阻负载图。

其中两纵向电容为两级放大器的容性负载，横向电容为包括Cgd结电容和补偿电容在内的密勒电容。

而且一般来说横向电容的值远大于两纵向电容。

这将可能使两个极点的位置相隔较远，从而可能可以采用某种近似来估算。

因此研究这样一个系统有实际意义。

（注意一个单纯这样的网络只

图8π形RC网络是一个微分器高通网络，适合放大器的两级π模型还应该加上一个压控电流源。

首先考察没有横向电容，仅有两个纵向电容的情况。

原理图如下：

图9两阶RC网络

这个原理图同上述π网络稍有不同。

注意到如果R2不是横向连接的话系统将为单极点系统（两个C并联为一个电容）。

为了使实验结果更加清晰，对这两个电容做了量级上的处理，即两纵向电容值分别为1u和1p，电阻值均为1k。

这样做的理由是使两个极点分离得比较远。

仿真得到系统包含两个极点1.592e2Hz以及1.592e8Hz，正好分别是

和

。

对于这个系统尚可用手算精确求得极点所在。

运用KVL和KCL，最后求解极点方程：

在C1>>C2的假设下，这个方程的解可以近似得到为1/R1C1和1/R2C2，与仿真结果相同。

但是应该看到，在两级时间常数相近的情况下，无法运用以上近似。

该传输函数的频率响应图如下：

图10两阶RC系统幅频、相频响应图

从上图中可以得到以下结论：

1）低频时幅度为0，相位也为0°；-3dB带宽为159Hz，即为第一极点所在（称为主极点），主极点对应相位为-45°；主极点之后的一段幅度响应呈现-20dB/十倍频特性。

这些结论同前面得到的结论类似。

2）由于经过设计，使两个极点分离较远，因此在频率f满足p0<

3）幅度响应曲线存在明显的拐点。

第二极点处（次极点）对应相位为-135°，即在-90°平台的基础上再次移动-45°，在幅度响应对应次极点处向上移动3dB，可以看到近似为幅度响应曲线的拐点所在。

该拐点对应的相位点无明显特征。

4）次极点之后的幅度响应呈现-40dB/十倍频的特征，可以证明为两个极点对幅度响应的效果的叠加。

对相位响应，在经过一定的相移之后相位响应稳定于-180°可以预期每个极点将使相位响应最终相移-90°。

根据上述得到的幅频、相频响应曲线可以进行一些推测和思考。

1）由于极点对幅度响应的影响表现为-20dB/dec，因此对一个实际的放大器来说，如果知道了低频增益Av和主极点，如果在主极点和第二极点之间不存在其他极零点的影响（关键是主极点和次极点之间不存在一个正零点），那么知道了Av和主极点，就可以对放大器的单位增益带宽做一个预期，如采用-20dB/dec或-6dB/octave估算。

但从根本上这样估算的理由是放大器的带宽增益积是一个常数。

2）值得注意的是放大器的单位增益带宽点不是也不应该是次极点，与相位的对应（关系到相位裕度）也没有直接的关系。

相关实验将在后面说明。

3）回想相位裕度的定义是放大器在单位增益带宽处对应的相位值同-180°（-180°还是0°需要看低频相位）的差。

因此，如果放大器的单位增益带宽恰好就是次极点的所在，那么相位裕度为45°，正好够了闭环稳定性的下限。

考虑到实际中45°的取值是绝对不够的，应该提供更大的相位裕度如65°，则单位增益带宽点应该在次极点之内。

——这也是单位增益带宽不应该是次极点的理由。

同时可以推论，次极点实际决定了放大器的最大带宽。

因此，如果AC仿真的带宽范围是从低频到单位增益带宽处，应该看到-20dB/dec才是理想情况（实际中可能包含极零点对，这样的响应很难得到）。

4）进一步推论：

由于单极点系统相位最终将停留在90°，故单极点系统总是闭环稳定的，即相位裕度至少为90°。

4．单级共源、电阻负载、有输入阻抗的单管放大器频率响应

左图是一个单级共源放大器，为了将问题简单化，没有采用实际中使用的有源负载或者二极管负载。

这样可以减少负载管结电容的影响。

Rs为信号源内阻，

在计算放大器频率响应时，一般会用到密勒定理，即对于连接输入和输出的电容（相当于反馈电容，本例中为Cgd）Cf来说，当考虑输入端时间常数时，等效为输入端并联一个电容为Cm=（1+|Av|）Cf的电容，同时可以取消反馈电容；而考虑输出端时间常数时，等效为在输出端并联一个电容为

的电容。

这样可以化为两个简单的一阶RC系统进行估算，将问题简化。

不过应该注意的是两个等效（输入端和输出端）不能同时使用，即当估算输入端时间常数时，输出端仅应并联实际的负载电容，不应再考虑Cm=（1-1/Av）Cf电容的影响。

而且应注意密勒定理仅能用来快速估算输入、输出时间常数，而将会漏掉一个零点，即密勒定理只考虑了极点情况而没有考虑零点情况。

但在实际应用中，密勒定理仍有实际价值，因为对放大器的频率响应常常更关心极点的情况。

首先采用密勒定理估算放大器的极点情况。

采用analogLibn33模型仿真。

输入nmos管为8u/0.4u，Rs=100k，负载电阻RL=5k。

低频增益|Av|=6.2，mos管跨导gm=1.33485m。

其中由仿真得到输入电容Cgs=11.3661f，Cdb=1.09277a，Cgd=3.0496f，Cgb=1.04188f。

仿真得到两个极点，分别为：

p0=4.61588e7Hz，p1=1.15656e10Hz，得到一个零点为z0=6.82626e10Hz。

对于输入端，输入电容为Cin=Cgs+Cgb+Cgd（1+|Av|）=34.3651fF

于是

（Hz）

输出端电容为Cout=Cdb+Cgd（1-1/Av）=2.558f

于是

（Hz）

可见上述估算基本同仿真结果相近。

（问题：

上面采用的模型为analogLibn33模型（ms018_v1p6_spe.lib:

sectiontt）这是一个比较理想的模型。

但当采用Print-〉DCOperatingPoint查看mos管电容参数时，发现对同一参数存在两个不同的电容值，例如对于栅漏交叠电容Cgd来说，理想情况下应该Cgd=Cdg，但实际列出的参数中同时包括Cgd和Cdg两个电容而且电容值不相同，不仅如此，对于mos管的各寄生电容均存在上述现象。

特别是当选用实际与工艺相结合的仿真库Chartered时，某些参数差别还比较大。

下面列出了对于同一W/L的nmos管，三种仿真库下各寄生电容的值的一个初步比较：

表1三种工艺相同W、L下管寄生电容值的比较

analogLibn33

Charterednmos_3p3

TSMCnch

Cgs

11.3661f

12.1048f

16.6876f

Csg

10.5613f

7.74032f

15.9375f

Cgd

3.0496f

1.72643f

2.29285f

Cdg

3.0669f

5.23175f

2.37264f

Cdb

1.09277a

992.412a

2.22305a

Cbd

4.43654a

10.191a

13.3451a

对于Cgd和Cdg存在两种名字，仿真器说明文档里给出的解释是

，

。

其他情况以此类推，包括列出的参数中包括的Cgg、Cdd、Css、Cbb等一系列电容。

对于同节点电容电容值有差别的原因，一方面可以采用上述公式加以解释，另一方面，还有更极端的例子，如针对40u/2u大尺寸nmos管，见下面列表：

表2成对电容参数的显著性差别示例

analogLibn33

Charterednmos_3p3

TSMCnch

Cgs

283.156f

261.629f

340.625f

Csg

253.674f

145.026f

330.117f

Cgd

15.4306f

8.96913f

11.8801f

Cdg

15.507f

97.0139f

12.1985f

Cdb

44.2014a

31.7396f

68.7948a

Cbd

11.0283a

15.2231a

5.42101a

注意到TSMC的各个参数都比较接近（除了Cdb和Cbd——但总归都是可以忽略的量级，不产生实际影响），而注意到Chartered的各项参数，有的已经有量级上的变化，比如Cdb和Cbd，其中Cdb的这个数值已经不能忽略！

可能的解释：

1）Chareted的工艺的不稳定性，比如漏电流大（？

）2）0.35工艺和0.25、0.18工艺上的不同（？

）

以上问题还有待进一步研究。

）

以上是采用密勒定理对放大器极点情况进行的一个估算。

但是在手算估算阶段欲估算放大器的极点情况，则需要首先估算出各节点的电容值，特别是Cgs和Cgd。

公式给出

，

，以下试验了几个不同的WL值，分析如下：

（采用Charterednmos_3p3库进行分析）

表3不同W、L，栅源电容、栅漏电容值的分析与扫描

W（um）

L（um）

Cgs（fF）

Cgd（fF）

Cgs/（WL）

Cgd/W

Csg

Cdg

Csg/WL

Cdg/W

8

1

27.27

1.374

3.409

0.17179

15.56

10.04

1.946

1.255

8

1.5

39.42

1.343

3.285

0.16789

22.10

14.37

1.842

1.796

8

2

51.49

1.329

3.218

0.16609

28.64

18.71

1.790

2.339

8

4

99.41

1.309

3.107

0.16361

54.78

36.12

1.712

4.515

16

4

200.7

2.683

3.136

0.1677

110.4

72.86

1.725

4.554

20

4

251.4

3.390

3.143

0.16951

138.3

91.25

1.728

4.563

30

4

378.2

5.229

3.152

0.17429

207.8

137.3

1.732

4.577

40

4

505.1

7.198

3.157

0.17996

277.4

183.5

1.733

4.587

如上表所示，对于Cgs，Cgs/（WL）给出的值近似为一个常数，注意到在WL比较小时，这个常数离平均值的偏差较大，而当WL较大时，常数的一致性较好，这可能是由于在栅面积比较小（WL比较小）时，边缘电容效应的影响比较大。

对于Cgd，Cgd/W的值常数一致性尚可。

说明利用上述公式来估算Cgs、Cgd的值还是可行的。

对于Csg参数，逆推得到的常数值同Cgs明显不同，基本上为1.8倍关系，但在WL较大时，常数一致性也比较好（WL较小时分析如前），说明对于Csg，手算估算也是可能的。

但对于Cdg电容，虽然在L=4时，常数性较好，但对于L=4以下的值，明显偏离了Cdg同W之间的线性预期。

说明对短沟道器件，估算Cdg是比较困难的。

关于Cdg的估算，还需要做进一步分析和扫描。

由以上分析可以看到，精确的由手算来估计Cdg等参数的值是比较困难的，而且后面将会看到，某些情况的极点需要采用Cdg来进行计算，因此这是另一个问题。

另外，对于Cdb电容，书上也给出了其值的计算公式，但考虑到这个值一般都会被忽略掉（对Chartered工艺不是这样），故没有对这个公式进行考察。

虽然用公式可能无法对Chartered的某些电容参数进行预估，但是后面将会看到，其影响不会太大，因为随着电路的复杂化，仅用手算来估计极点的值将是不现实的。

Gray一书推荐的正确地进行极零点分析以及进行补偿的方法是：

先采用计算机模拟仿真得到原始的极零点情况，然后估计补偿电容的值，加入电路中进行仿真，观察极零点情况，然后进行进一步调整并迭代以上步骤。

因此包括Cgd同Cdg值不同，手算无法估算等问题，在实际应用中将会被仿真所解决。

Gray一书上对上述电路给出了精确的推导和最后的极点公式，由于密勒等效估算的结果同实际值比较接近，因此未对此精确公式（比较复杂）进行验证。

但是精确的公式给出了单零点的所在：

z0=gm/Cgd，仿真给出z0=6.82626e10Hz，手算给出

Hz，精度尚可。

但应注意，此处估算应该采用Cdg而非Cgd的电容值，比如针对一个极端例子输入管为40u/2u的nmos_3p3Chartered器件，只能采用97f的Cdg来计算零点值，并且手算结果精度较好，当采用8f的Cgd值来计算零点值时，很明显产生量级上的偏差。

这个例子说明仿真器的确是区分了两个电容值的，而且对Chartered工艺，区分很显著（由于TSMC工艺成对参数都比较一致，故无法验证）。

后面的例子还将进一步给出使用Cgd和Cdg两种情况的比较并推测其使用场合。

下面是这个放大器的频率响应仿真曲线图：

（analogLibn33库）

图12单管共源放大器（非理想信号源）输出点频率响应曲线图

一些结论并不赘述。

从图中可以进一步确定前面的几个推论：

1）主极点46.2MHz处为-3dB带宽，对应相位约135°（由于反相输出，初始相位为180°，主极点仍然使相位响应相移-45°）。

次极点11.6GHz（对应相位约为45°，沿第一极点产生的90°平台再产生-45°相移）向上3dB处恰为幅度响应拐点。

零点68.3GHz处（对应相位约为-45°，即沿第二极点产生的0°相位平台再产生-45°相移）向上3dB处为曲线的另一个拐点。

第一拐点将幅频曲线向下拐至斜率-40dB/dec，第二拐点将曲线重新上抬至斜率-20dB/dec。

只是由于次极点和零点之间分的不是太开，故其间的-40dB/dec斜率并不准确，因为在这一频率范围内并不能忽略除主极点之外的其他极点而将传输函数进行对数化简。

（可以仿前例证明）

2）可以看到该系统的单位增益带宽为281MHz，在主极点和次极点之间，且与相位没有直接关系。

这证明了次极点并不是单位增益带宽点。

该系统的相位裕度为97.8°。

可以想象，如果能将主极点和次极点以及正零点显著分开，则系统在单位增益频率内等价为一个单极点系统，从而单位增益带宽处，相位响应将停留在90°平台处，系统相位裕度为90°，将必然稳定。

这是放大器设计的最理想情况。

对于正在设计中的折叠共源共栅放大器的两个增益辅助放大器来说，一般应该呈现这样的幅频响应特性。

同时可以想象，如果不幸放大器的单位增益带宽点落在了次极点之外，相位裕度将必然小于45°，放大器在闭环工作时将必然振荡。

此时就需要加入补偿电容，调节系统的极零点的值，使其满足相位裕度和稳定性的要求。

5．单级共源放大器各种形式频率响应的实验验证

5.1单级共源、电阻负载、有输入阻抗的单管放大器频率响应

左图为一个理想电压源驱动的单管共源放大器的原理图。

由于去掉了Rs内阻，从而上例中输入端时间常数不存在，即系统变为单极点、单零点系统。

并且由于没有密勒效应（因为不需要考虑输入端时间常数），使得小信号模型比较简单，可以推得极零点的精确公式。

零点公式同前，为

，注意此处仍为Cdg。

此例中mos管参数均不变，故零点频率与上例相同，且手算结果与仿真较接近。

图13理想Vin单管

对于极点计算，Baker一书给出的计算公式为

，其中

，除去Cgd和Cdg的区别，按此公式计算出的极点位置与仿真得到的偏差较大。

为了得到极点的准确表示，采用将负载电容显著化的方法，首先忽略掉管寄生电容的影响，即在输出端并联1pF电容，这将预期远大于寄生电容值。

并将Cgd同Cdg的差别显著化，采用40u/2u的管参数，如前所述，此参数下Cgd=9fF，Cdg=97fF。

此时为使管正常工作，负载电容为3.5k，管跨导gm=1.50164m。

即

，Rl=3.5k，

。

当输出端并联1pF电容，并采用40u/2u管参数时，仿真得到极点值为4.394e7Hz，逆推可知此极点应采用公式

计算，手算极点值为4.547e7Hz。

去掉负载电容逆推电容的具体表示发现电容项应采用

计算较为正确（同样可以采用将Cgd显著化的方法验证），其中Cjd为漏体节电容（Drain-bulkjunctioncapacitance）。

且此公式对于TSMC仿真库同样适用，但对于analogLib库，以上公式均不正确且存在量级上的差别。

可能原因是analogLib仿真库并不是一个同实际工艺相结合的仿真库。

另外仿真器此处采用Cjd电容值而其他地方未采用的原因不明，不过进一步的探索意义不大。

通过上面两例的比较可以看到，信号源是否为理想信号源决定了放大器极点的具体计算方法。

由于在功能设计仿真时，一般认为输入信号源为理想信号源，即输入管栅上都没有串接电阻，故由第二个例子可以看到，放大器的主极点将由输入管的栅漏交叠电容、下级负载电容以及输入级负载所决定（否则将由信号源内阻以及输入级密勒电容决定）。

而实际中输入信号源的负载应该是一个比较小的值（比较接近理想情况），故实际极点的取值将比较接近第二种情况。

5.2单管放大器有源负载等形式的验证

5.2.1非理想信号源有源负载单级放大电路

各管参数：

负载pmos管12u/0.4uCgs2=17.1283f，Cbd2=7.9a，输入nmos管40u/2u，Cgd1=8.81f，Cdg1=96.855f，Cbd1=14a，Cgs1=261.628f，Csg1=145.026f。

gm1=1.50193m，Av=1.60，gm2=886.1u

仿真得到p0=5.31e6，p1=2.22e9，z0=2.47e9

手算零点：

=2.469e9

主极点：

（注意此处应采用Cgs1而非Csg1）

图14非理想信号源有源负载

=5.59e6

次极点：

=1.820e9

可见结果尚在接受范围之内。

5.2.2理想信号源有源负载单级放大电路

各管参数不变，仿真得到单极点p0=2.028e9，单零点z0=2.468e9。

Cjd1=37.0427f，Cjd2=14.5554f

零点计算公式同前，且管参数未变，省去验证步骤。

主极点

=2.229e9

5.2.3理想信号源电流源负载单级放大电路

如左图，管参数全部不变，仅将有源负载换为电流源负载，并采用与原输出电压相近的栅极偏置电压。

仿真得到Av=28.85，主极点1.312e8，零点位置不变。

其中gm2=866.011u（不变），gds2=49.0085u，Cds2=5.81306f

=1.178e8

注意到此处应采用gds2而非gm2，即应采图15理想信号源电流源负载用电流源负载的小信号输出电阻。

5.2.4非理想信号源电流源负载单级放大电路（略）

由上述同尺寸的有源负载结构同电流源负载结构的比较中可以看出，有源负载结构的增益通常不大（可以证明当输入和输出直流电位均为中点点位（1.65V）时，有源负载结构约为1（Chartered工艺为0.8左右，同P管和N管阈值电压相关）），但因此频率性能比较好（主要是因为P有源负载管小信号输出电阻小，为

，即输出负载电阻小），如例5.2.