结构力学之平面体系的几何组成分析.ppt

结构力学之平面体系的几何组成分析.ppt

《结构力学之平面体系的几何组成分析.ppt》由会员分享，可在线阅读，更多相关《结构力学之平面体系的几何组成分析.ppt（43页珍藏版）》请在冰豆网上搜索。

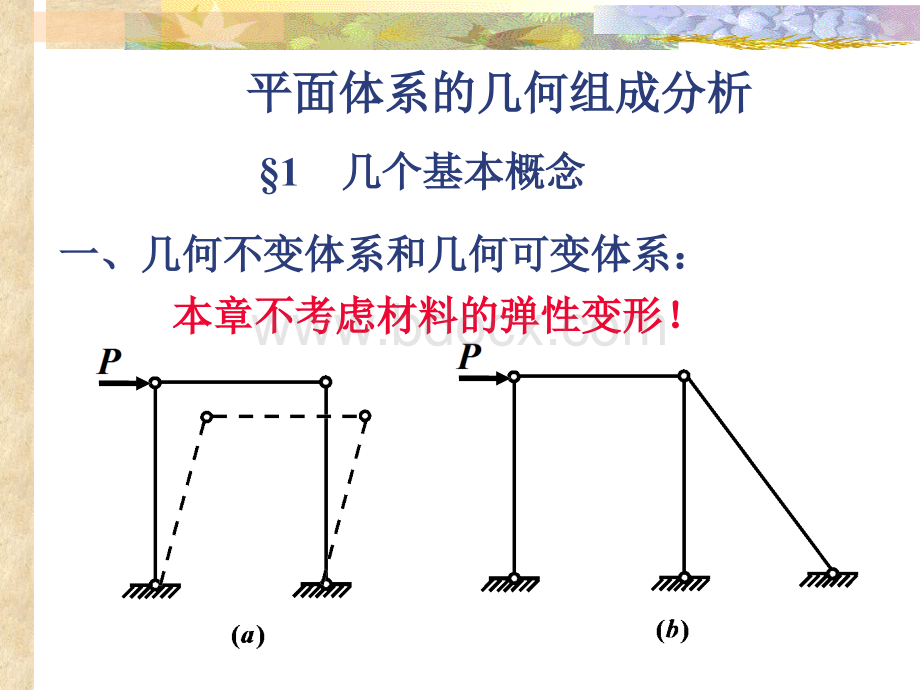
平面体系的几何组成分析平面体系的几何组成分析一、几何不变体系和几何可变体系：

一、几何不变体系和几何可变体系：

本章不考虑材料的弹性变形！

本章不考虑材料的弹性变形！

1几个基本概念几个基本概念几何不变体系：

几何不变体系：

是在荷载作用下，在不考虑是在荷载作用下，在不考虑材料的弹性变形的前提下，位置和几何形状材料的弹性变形的前提下，位置和几何形状保持不变的体系。

保持不变的体系。

几何可变体系：

几何可变体系：

是在荷载作用下，即使在不是在荷载作用下，即使在不考虑材料的弹性变形的前提下，位置和几何考虑材料的弹性变形的前提下，位置和几何形状也会发生改变的体系。

形状也会发生改变的体系。

只有几何不变体系才能作为结构而被采用。

只有几何不变体系才能作为结构而被采用。

二、刚片和链杆的概念：

二、刚片和链杆的概念：

（一）刚片：

（一）刚片：

刚体在平面上的投影就是刚片刚体在平面上的投影就是刚片。

任何一个几何不变部分都可以看作是任何一个几何不变部分都可以看作是一个刚片。

一个刚片。

比如：

比如：

一根梁，一根梁，基础基础

（二）链杆：

（二）链杆：

两端仅用铰与其它部分相联的两端仅用铰与其它部分相联的单个构件单个构件，几何不变部分几何不变部分刚片刚片用用表示。

表示。

三、自由度：

三、自由度：

确定体系位置所需要的独立坐标数目。

确定体系位置所需要的独立坐标数目。

平面内点的自由度为平面内点的自由度为2点：

点：

2刚片：

刚片：

平面内刚片的自由度为平面内刚片的自由度为33四、约束（联系）：

四、约束（联系）：

减少自由度的装置。

减少自由度的装置。

一根链杆一根链杆把一个刚片和基础相连，这时把一个刚片和基础相连，这时3-=1一根链杆相当于一个约束。

一根链杆相当于一个约束。

刚片的自由度为多少？

刚片的自由度为多少？

22单铰单铰：

一个单铰相当于一个单铰相当于2个约束。

个约束。

仅联结两个刚片的铰叫单铰仅联结两个刚片的铰叫单铰。

3-=21从约束的角度讲：

从约束的角度讲：

一个单铰相当于两根一个单铰相当于两根链杆的作用链杆的作用。

五、多余约束：

五、多余约束：

增加约束不能减少自由度，增加约束不能减少自由度，这种约束叫多余约束。

这种约束叫多余约束。

在在几何不变体系几何不变体系中，如果撤除某些约束中，如果撤除某些约束后，体系仍为几何不变的，则称可以撤后，体系仍为几何不变的，则称可以撤除的约束是多余约束。

除的约束是多余约束。

一、三刚片规则：

一、三刚片规则：

2几何不变体系的基本组成规则几何不变体系的基本组成规则三个刚片用不在同一直线上的三个单铰两三个刚片用不在同一直线上的三个单铰两同一时刻同一时刻9-=3633=932=6两相联，所组成的体系是几何不变体系，两相联，所组成的体系是几何不变体系，且无多余约束。

且无多余约束。

三个刚片用不在同一直线上的三个单铰两三个刚片用不在同一直线上的三个单铰两两相联，所组成的体系是几何不变体系，两相联，所组成的体系是几何不变体系，且无多余约束。

且无多余约束。

例一、例一、1、找刚片：

、找刚片：

视视ADC为刚片为刚片I，BEC为为刚片刚片II，基础为刚片基础为刚片III。

、拉关系：

、拉关系：

刚片刚片I和和刚片刚片II用用C铰相铰相试对图示体系作几何组成分析：

试对图示体系作几何组成分析：

、用规则，下结论：

、用规则，下结论：

根据三刚片规则，该体系是几根据三刚片规则，该体系是几联，刚片联，刚片I和刚片和刚片III用用A铰相联，刚片铰相联，刚片II和刚片和刚片III用用B铰相连。

铰相连。

何不变体系，且无多余约束。

何不变体系，且无多余约束。

解：

解：

从约束的角度讲，一个单铰相当于两根从约束的角度讲，一个单铰相当于两根链杆的作用。

链杆的作用。

同时联结两个刚片的两根链杆相当于同时联结两个刚片的两根链杆相当于一个单铰的作用。

一个单铰的作用。

实交实交平行平行延长线相交延长线相交实铰虚铰瞬铰例二、例二、解：

解：

试对图示体系作几何组成分析：

试对图示体系作几何组成分析：

1、找刚片：

、找刚片：

视视ABC为刚片为刚片I，CDEF为为、拉关系：

、拉关系：

刚片刚片II和刚片和刚片III用两根链杆，相当于虚铰用两根链杆，相当于虚铰D相联。

相联。

刚片刚片II，基础为刚片基础为刚片III。

刚片刚片I和刚片和刚片II用用C铰相联，铰相联，刚片刚片I和刚片和刚片III用用A铰相联，铰相联，、用规则，下结论：

、用规则，下结论：

根据三刚片规则，该体系是几根据三刚片规则，该体系是几何不变体系，且无多余约束。

何不变体系，且无多余约束。

二、二刚片规则：

二、二刚片规则：

两个刚片用既不全平行也不全交于一点的两个刚片用既不全平行也不全交于一点的三根链杆相联，所组成的体系是几何不变三根链杆相联，所组成的体系是几何不变体系，且无多余约束。

体系，且无多余约束。

推论：

推论：

两个刚片由一个铰和一根轴线不通过该铰的两个刚片由一个铰和一根轴线不通过该铰的链杆相联，所组成的体系是几何不变体系，链杆相联，所组成的体系是几何不变体系，且无多余约束。

且无多余约束。

例三、例三、分析图示体系的几何构造：

分析图示体系的几何构造：

解法一：

解法一：

1、找刚片：

、找刚片：

视视ABCD为为刚片刚片I，基础为刚片基础为刚片II。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II用既不全平行，也用既不全平行，也不全交于一点的三根链杆相联。

不全交于一点的三根链杆相联。

、用规则，下结论：

、用规则，下结论：

根据二刚片规则，该体系是几何根据二刚片规则，该体系是几何不变体系，且无多余约束。

不变体系，且无多余约束。

解法二：

解法二：

1、找刚片：

、找刚片：

视视ABCD为为刚片刚片I，基础为刚片基础为刚片II。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II用铰用铰A和一根轴线和一根轴线不通过铰不通过铰A的链杆的链杆BE相联。

相联。

、用规则，下结论：

、用规则，下结论：

根据二刚片规则的推论根据二刚片规则的推论，该体系该体系是几何不变体系，且无多余约束。

是几何不变体系，且无多余约束。

体系与基础的联结满足两体系与基础的联结满足两简支刚架简支刚架简支梁简支梁叫简支结构。

叫简支结构。

刚片规则或其推论的结构刚片规则或其推论的结构简支刚架简支刚架例四、例四、分析图示体系的几何构造：

分析图示体系的几何构造：

解法一：

解法一：

1、找刚片：

、找刚片：

视视AB为刚片为刚片I，基础为刚片基础为刚片II。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II用全交于一点的用全交于一点的三根链杆相联。

三根链杆相联。

、用规则，下结论：

、用规则，下结论：

根据二刚片规则，该体系是几何根据二刚片规则，该体系是几何可变体系。

可变体系。

1、找刚片：

、找刚片：

视视AB为刚片为刚片I，基础为刚片基础为刚片II。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II用铰用铰A和一根轴线和一根轴线通过铰通过铰A的链杆的链杆BC相联。

相联。

、用规则，下结论：

、用规则，下结论：

根据二刚片规则的推论根据二刚片规则的推论，该体系该体系是几何可变体系。

是几何可变体系。

解法二：

解法二：

三、二元体规则：

三、二元体规则：

（一）什么是二元体？

（一）什么是二元体？

二元体：

两根不共线的链杆联结一个新结点二元体：

两根不共线的链杆联结一个新结点的设置。

的设置。

书写：

书写：

二元体二元体A-C-B。

（二）二元体规则：

（二）二元体规则：

增加或去掉二元体不改变原体系的几何增加或去掉二元体不改变原体系的几何组成性质。

组成性质。

例五、例五、解：

解：

基本铰结三角形基本铰结三角形ABC符合符合分析图示体系的几何构造：

分析图示体系的几何构造：

三刚片规则，是无多余约三刚片规则，是无多余约束的几何不变体系；束的几何不变体系；依次依次在其上增加二元体在其上增加二元体A-D-C、C-E-D、C-F-E、E-G-F后，后，体系仍为几何不变体，且体系仍为几何不变体，且无多余约束。

无多余约束。

3几何组成分析示例几何组成分析示例一、依据：

一、依据：

通常，把判断某个体系是否几何可变通常，把判断某个体系是否几何可变的过程，叫做几何构造分析。

的过程，叫做几何构造分析。

几个规则及推论几个规则及推论二、步骤：

二、步骤：

1、找刚片：

、找刚片：

、拉关系：

、拉关系：

、用规则，下结论：

、用规则，下结论：

三、示例：

分析图示各体系的几何构造：

三、示例：

分析图示各体系的几何构造：

例一、例一、1、找刚片：

、找刚片：

视视ABCD为刚片为刚片I，DEFG为刚为刚片片II，基础为刚片基础为刚片III。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II通过通过D铰相联，铰相联，、用规则，下结论：

、用规则，下结论：

根据三刚片规则，该体系是无多余约束根据三刚片规则，该体系是无多余约束的几何不变体系。

的几何不变体系。

解：

解：

刚片刚片I和刚片和刚片III通过通过A铰相联，铰相联，刚片刚片II和刚片和刚片III通过虚铰通过虚铰G相联。

相联。

例二、例二、凡上部体系与基础的凡上部体系与基础的1、找刚片：

、找刚片：

视视AB为刚片为刚片I，CE为刚片为刚片II。

、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II通过四根既不全平行，通过四根既不全平行，、用规则，下结论：

用规则，下结论：

上述几何不变体系与基础按照上述几何不变体系与基础按照解：

解：

该体系是有一个多余约束的几何不变体系。

该体系是有一个多余约束的几何不变体系。

联结满足两刚片规则联结满足两刚片规则时，可先不考虑基础，时，可先不考虑基础，分析剩余部分。

分析剩余部分。

也不全交于一点的链杆相联，组成一也不全交于一点的链杆相联，组成一个有一个多余约束的几何不变体系。

个有一个多余约束的几何不变体系。

二刚片规则组成新的几何不变二刚片规则组成新的几何不变体系。

体系。

有一个多余约束的几何可变体系；与基础相联后，有一个多余约束的几何可变体系；与基础相联后，仍是有一个多余约束的几何可变体系。

仍是有一个多余约束的几何可变体系。

后仍为几何不变体系后仍为几何不变体系，AD是多余约束；因此，是多余约束；因此，ABCD是有一个多余约束的几何不变体系是有一个多余约束的几何不变体系，视为刚片视为刚片I；EF视为刚片视为刚片II。

例三、例三、解：

解：

1、找刚片：

、找刚片：

基本铰结三角形基本铰结三角形ABC，增加二元增加二元B-D-C、拉关系：

、拉关系：

刚片刚片I和刚片和刚片II用两根链杆相联。

用两根链杆相联。

、用规则，下结论：

用规则，下结论：

根据二刚片规则，上部体系是根据二刚片规则，上部体系是四、几种情况：

四、几种情况：

（一）两刚片用三根全平行的链杆相联；

（一）两刚片用三根全平行的链杆相联；、三根链杆等长；、三根链杆等长；常变体系常变体系、三根链杆不等长；、三根链杆不等长；瞬变体系瞬变体系微小位移后即成为几何不微小位移后即成为几何不变的体系。

变的体系。

原为几何可变的，经原为几何可变的，经请大家思考：

请大家思考：

瞬变体系能否作为结构瞬变体系能否作为结构而被采用？

而被采用？

（二）两刚片用全交于一点的三根链杆相联。

（二）两刚片用全交于一点的三根链杆相联。

、三根链杆实交于、三根链杆实交于一点；一点；、三根链杆延长线、三根链杆延长线交于一点；交于一点；常变体系常变体系瞬变体系瞬变体系（三）联结三个刚片的三个铰在同一直线上：

（三）联结三个刚片的三个铰在同一直线上：

瞬变体系瞬变体系在这一瞬时在这一瞬时瞬变体系能否作为结构而被采用？

瞬变体系能否作为结构而被采用？

1、由于内力太大，杆、由于内力太大，杆瞬变体系绝对不能作为结构被采用。

瞬变体系绝对不能作为结构被采用。

件被破坏。

件被破坏。

2、杆件变形很大，虽、杆件变形很大，虽不破坏，但受力情不破坏，但受力情况很恶劣。

况很恶劣。

五、几何组成分析中的一些技巧及其示例：

五、几何组成分析中的一些技巧及其示例：

例一、例一、这类体系叫多跨梁。

这类体系叫多跨梁。

技巧一：

技巧一：

每次先考察体系的一部分刚片，在每次先考察体系的一部分刚片，在该部分应用基本规则，把已经组成的几何不变该部分应用基本规则，把已经组成的几何不变部分当作刚片。

部分当作刚片。

无无多多余余约约束束的的几几何何不不变变体体系系。

首先分析基础与多跨梁中的哪一段首先分析基础与多跨梁中的哪一段组成了几何不变体系。

组成了几何不变体系。

例二、例二、无多余约束的几何不变体系无多余