ch065潮流计算.docx

ch065潮流计算.docx

《ch065潮流计算.docx》由会员分享，可在线阅读，更多相关《ch065潮流计算.docx（15页珍藏版）》请在冰豆网上搜索。

ch065潮流计算

第6.5章潮流计算

一、节点电压方程与节点导纳矩阵

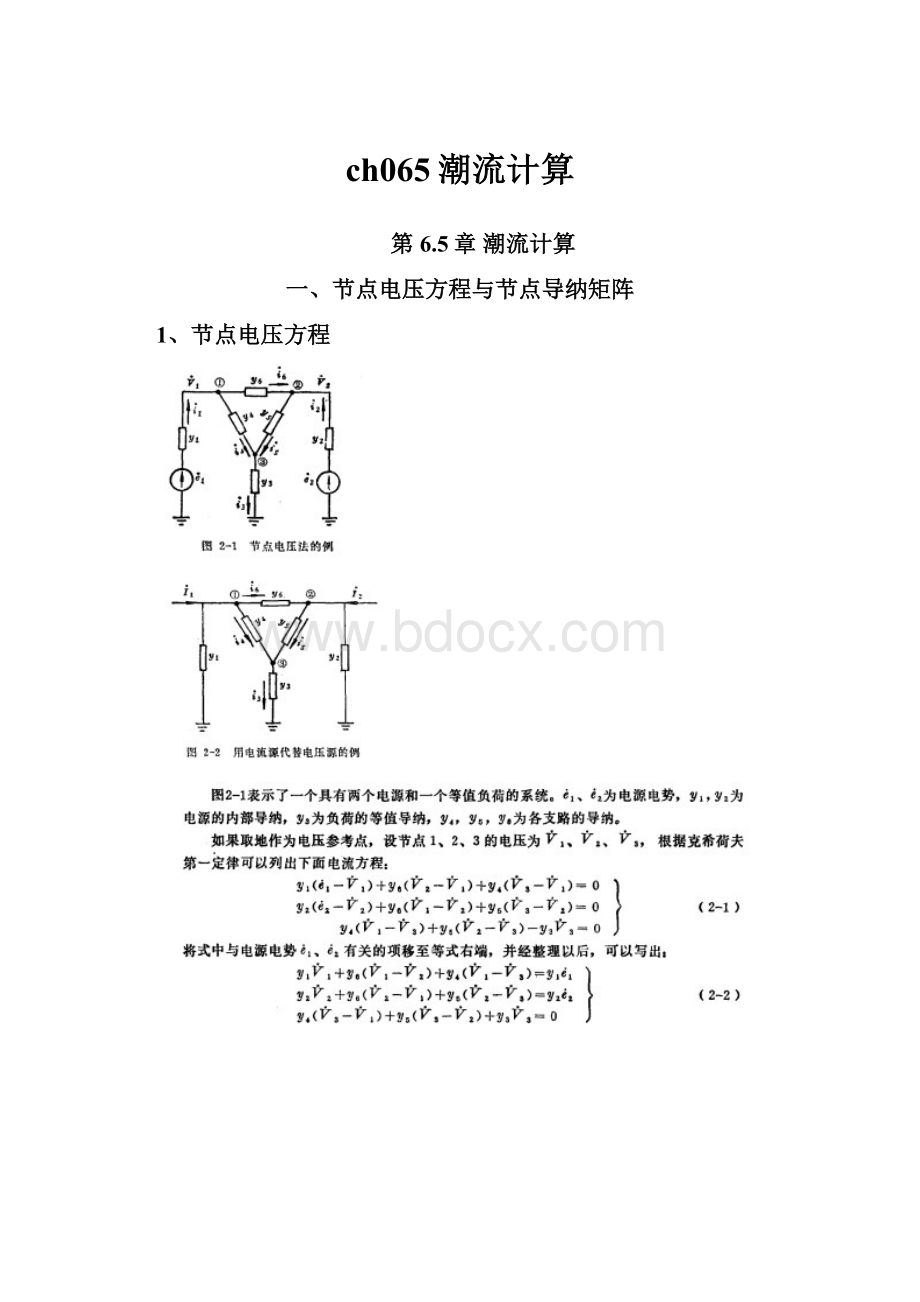
1、节点电压方程

为节点导纳矩阵，其中对角元素Yii为节点i的自导纳，非对角元素Yij为节点i与节点j之间的互导纳。

2、节点导纳矩阵

如前所述，在利用电子数字计算机计算电力系统运行情况时，多采用式（2—5）形式的节点方程式，其阶数等于电力网络的节点数。

将它展开可写成一般的形式：

它反映了电力网络的参数及接线情况，因此导纳矩阵可以看成是对电力网络电气特性的一

种数学抽象。

由导纳短阵所连系的节点方程式是电力网络广泛应用的一种数学模型。

（1）节点导纳矩阵的物理意义：

导纳矩阵中第i列对角元素yii，即节点i的自导纳，在数值上等于节点i加单位电压，其它节点都接地时，节点i向电力网络注入的电流。

导纳矩阵中第i列非对角元素yij，即节点i与节点j间的互导纳，在数值上等于节点i加单位电压，其它节点都接地时，节点j向

电力网络注入的电流。

（2）节点导纳矩阵的计算

（1）导纳矩阵的阶数等于电力网络的节点数；

（2）导纳矩阵各行非对角元素中非零元素的个数等于对应节点所连的不接地支路

数；

（3）导纳矩阵各对角元素，即各节点的自导纳等于相应节点所连支路的导纳之和；

（4）导纳矩阵非对角元素yij，等于节点i与节点j间支路的导纳取负号。

（3）算例

二、潮流计算问题的数学模型

电力系统由发电机、变压器、输电线路及负荷等构成。

图表示了一个简单电力系统的接线图。

在进行电气计算时，系统中静止元件如变压器、输电线、并联电容器、电抗器等可以用R、L、C所组成的等值电路来模拟。

因此，由这些静止元件所连成的电力网在潮流计算中可以看作是线性网络，并用相应的导纳矩阵或阻抗矩阵来描述。

在潮流计算中发电机和负荷都作为非线性元件来处理，不能包括在线性网络部分，如图3—1（5）所示。

如果联络节点在形成导纳矩阵或阻抗矩阵时没有消去，这种节点也作为注入零功率的节点引出网络之外。

图中虚线所包括的线性网络部分，其节点电流与电压之间的关系可以通过节点方程式来描述：

在电力系统潮流计算中，表征各节点运行状态的参数是该点的电压向量及复功率，也就是说，每个节点都有四个表征节点运行状态的量：

V、θ、P、Q，因此，在n个节点的电力系统中共有4n个运行参数。

如上所述，电力潮流基本方程式（3—6）或（3—7）共有n个复数方程式，相当于2n个实数方程式，因此只能解出2n个运行参数，其余2n个应作为原始数据事先给定。

在一般电力系统潮流计算时，对每个节点往往给出两个运行参数作为己知条件，而另

外两个则作为待求量。

根据原始数据给出的方式，电力系统中的节点分为以下三种类型：

（1）PQ节点‘

对这类节点给出的参数是该点的有功功率及无功功率（P、Q），待求量为该点的电压向量（V，θ）。

通常变电所母线都是PQ节点。

当某些发电厂的出力P，Q给定时，也作为PQ节点。

在潮流计算中，系统中大部分节点部属于这类节点。

（2）PV节点

这类节点给出的运行参数为该点的有功功率P及电压幅值V，待求量是该点的无功功率Q及电压向量的角度θ。

这种节点在运行中往往要有一定可调节的无功电源，用以维持给定的电压值。

因此，这种节点是系统中可以调节电压的母线。

通常选择有一定无功功率贮备的发电厂母线作为PV节点。

当变电所有无功补偿设备时，也可以作PV节点处理。

（3）平衡节点

在潮流计算中，这类节点一般在系统中只设一个。

对这个节点，我们给定该点的电压幅值，并在计算中取该点电压向量的方向作为参考轴，相当于给定该点电压向量的角度为零度。

因此，对这个节点给定的运行参数是V和θ，因此也可以称为Vθ节点。

对平衡节点来说，待求量是该点的有功功率P及无功功率Q，整个系统的功率平衡由这一节点来完成。

三、牛顿－拉夫逊潮流解法

1、牛顿－拉夫逊原理

2、节点功率方程组

代入，将上式按实部和虚部展开，得到：

这就是功率的极坐标方程式。

3、潮流解法

当采用极坐标的数学模型时，待求量是各节点电压的幅值和角度Vi，θi（i＝1，2，…，n）。

对PV节点来说，该节点电压幅值Vi是给定的，不再作为变量，同时，该点不能预先给定无功功率Qi，这样，方程式中ΔQi也就失去了约束作用。

因此，在选代过程中应该取消与PV节点有关的无功功率方程式。

只有当迭代结束后，即各节点电压向量求得以后，才利用这些方程式来求各PV节点应维持的无功功率。

同样道理，由于平衡节点电压幅值及角度都是给定量，因此，与平衡节点有关的方程式也不参与迭代过程。

迭代结束后，我们利用与平衡节点的方程式来确定平衡节点的有功功率及无功功率。

4、潮流解法程序步骤

四、PQ分解法

P—Q分解法（又称改进牛顿法）是从改进和简化牛顿法潮流程序的基础上提出来的，它的基本思想是：

把节点功率表示为电压向量的极坐标方程式，抓住主要矛盾，以有功功率误差作为修正电压向量角度的依据，以无功功率误差作为修正电压幅值的依据，把有功功率和无功功率迭代分开来进行。

牛顿法的修正方程式为：

以上方程式是从数学上推导出来的，并没有考虑电力系统这个具体对象的特点。

我们知道，电力系统中有功功率主要与各节点电压向量的角度有关，无功功率则主要受各节点电压幅值的影响。

大量运算经验也告诉我们，式（3—126）中矩阵N及J中各元素的数值相对是很小的，因此对牛顿法的第一步简化就是把有功功率和无功功率分开来进行迭代，即将式（3—126）简化为：

这样，由于我们把2％阶的线性方程组变成了二个9b阶的线性方程组，因而计算量和内存方面都有改善。

但是，如策3—4—3中指出的那样，H，L在迭代过程中仍然不断变化，而且又部是不对称矩阵。

对牛顿法的第二个简化，也是比较关键的一个简化，即把式（3—127）

中的系数短阵简化为在迭代过程中不变的对称矩阵。

众所周知，一般线路两端电压的相角差是不大的（通常不超过10。

一20。

），因此可以

认为：

以上两式就是P—Q分解法的修正方程式，其守系数矩阵只不过是系统导纳矩阵的虚部，因而是对称矩阵，而且在迭代过程中维持不变。

它们与功率误差方程式（3—96）：

表面看来，似乎式（3—135），（3—136）的系数矩阵是一样的，但在实际P—Q分解法程序中，两个修正方程式的系数短阵并不相同。

一般可以简写为：

为了改善P—Q分解法的收敛特性，B'一般并不严格是电力系统导纳矩导纳短阵的虚部，而B”则是由导纳短阵的虚部构成。

在B'中，忽略了线路和变压器的接地支路导纳。

修正方程式（3—141）应改变为以下的形式；

式中V0为系统乎均电压，也就是说修正方程式右端应以系统平均电压代替各节点的计算电压。

这实际上是减少在迭代过程中各节点计算电压对有功功率及电压向量角度迭代过程的影响。