理想气体典型例题.docx

理想气体典型例题.docx

《理想气体典型例题.docx》由会员分享，可在线阅读，更多相关《理想气体典型例题.docx（16页珍藏版）》请在冰豆网上搜索。

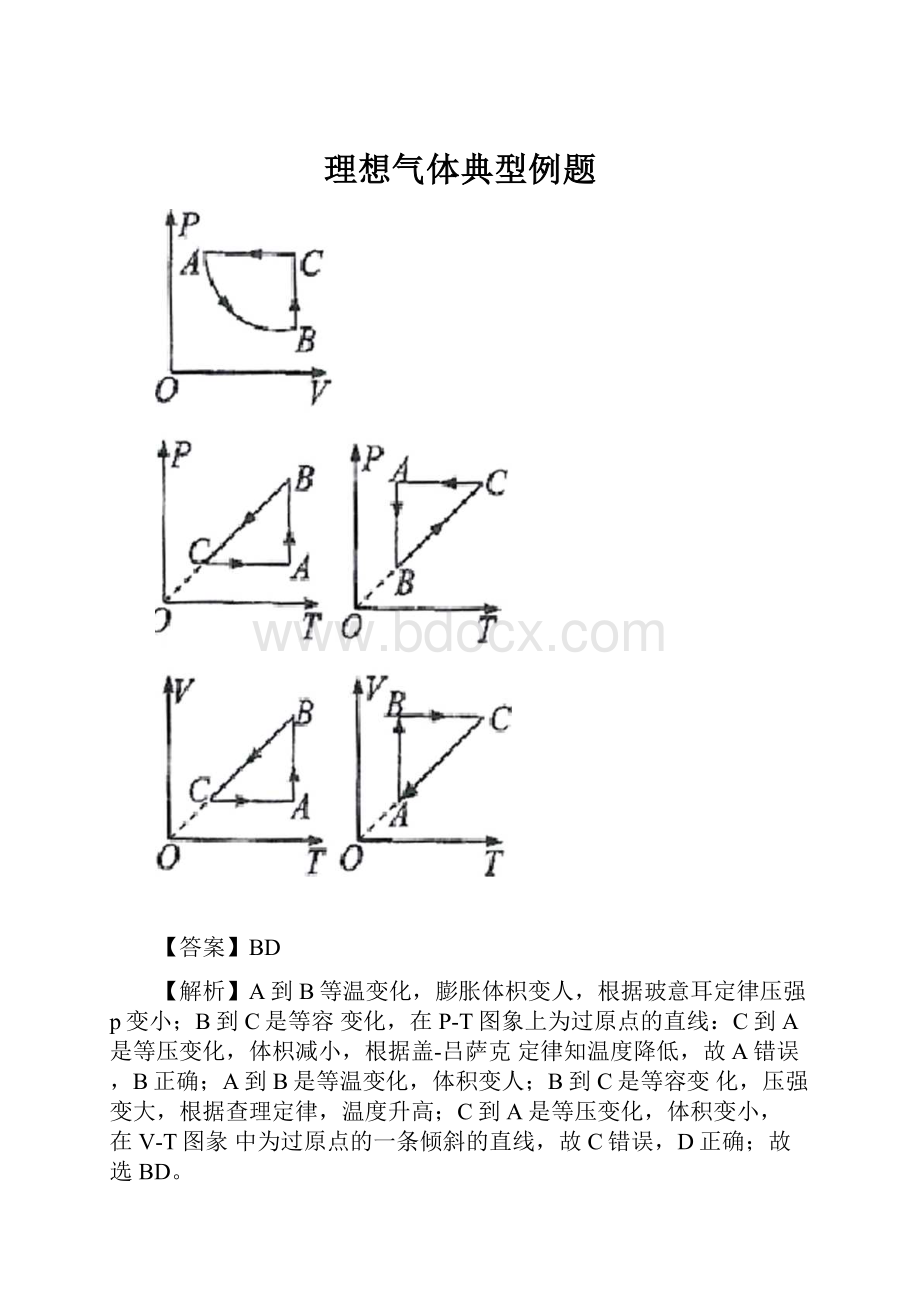
理想气体典型例题

【答案】BD

【解析】A到B等温变化，膨胀体枳变人，根据玻意耳定律压强p变小；B到C是等容变化，在P-T图象上为过原点的直线：

C到A是等压变化，体枳减小，根据盖-吕萨克定律知温度降低，故A错误，B正确；A到B是等温变化，体积变人；B到C是等容变化，压强变大，根据查理定律，温度升高；C到A是等压变化，体积变小，在V-T图彖中为过原点的一条倾斜的直线，故C错误，D正确；故选BD。

点睛：

本题要先根据P-V图线明确各个过程的变化规律，然后结合理想气体状态方程或气体实验定律分析P-T先和V-T线的形状.

2.水平玻璃细管A与竖直玻璃管B、C底部连通，组成如图所示结构，各部分玻璃管内径相同。

B管上端封有长20cm的理想气体，C管上端开II并与大气相通，此时两管左、右两侧水银面恰好相平，水银面距玻璃管底部为25cm.水平细管A内用小活塞封有长度10cm的理想气体.已知外界人气压强为75cmHg,忽略坏境温度的变化•现将活塞缓

慢向左拉，使B管内气体的气柱长度为25cm,

求A管中理想气体的气柱长度。

【答案】

【解析】活塞被缓慢的左拉的过程中，气体A做等温变化初态：

压强皿二（75+25）cmHg=100cmHg,体积V^IOS,末态：

压强皿二（75+5）cmHg=80cmHg,体积V^LazS根据玻意耳定律可得：

PzVai二Px：

V_C

解得理想气体A的气柱长度：

点睛：

本题考查气体实验定律的应用，以气体为研究对彖，明确初末状态的参量，气体压强的求解是关键，应用气体实验定律应注意适用条件.

3.一热气球体积为V,内部充有温度为T■的热空气，气球外冷空气的温度为T-已知空气在1个大气压、温度T。

时的密度为P。

，该气球内、外的气压始终都为1个大气压，重力加速度大小为g.

（i）求该热气球所受浮力的犬小；

（ii）求该热气球内空气所受的重力；

（iii）设充气前热气球的质量为m。

，求充气后它还能托起的最大质量.

【答案】（i）f=PoE（ii）G=Vgpfi~（iii）m=

Tb丁。

RTq

【解析】（i）设1个大气压下质量为加的空气在温度％时的体积为&密度为

温度为7时的体积为耳,密度为：

p（T）=^-②

由盖-吕萨克定律可得：

—=—③

ToT

联立①②③解得：

p（T）=几半④气球所受的浮力为：

f=p（Th）gV®

联立④⑤解得:

"警⑥

（ii）气球内热空气所受的重力：

G=p（T“）Vg⑦联立④⑦解得：

G=VgQ半⑧

1a

（iii）设该气球还能托起的最大质量为也，由力的平衡条件可知:

G-nkg®

联立⑥⑧©可得：

加=学-绰N-陆

【名师点睛】此题是热学问题和力学问题的结合题；关键是知道阿基米徳定律，知道温度不同时气体密度不同；能分析气球的受力情况列出平衡方程。

4.一种测量桶薄气体压强的仪器如图（a）所示，玻璃泡M的上端和下端分别连通两竖直玻璃细管怎和总。

區长为厶顶端封闭，总上端与待测气体连通：

"卞端经橡皮软管与充有水银的容器斤连通。

开始测量时，〃与总相通：

逐渐提升斤，直到总中水银面与&顶端等高，此时水银已进入心，且&中水银面比顶端低力，如图（b）所示。

设测量过程中温度、与金相通的待测气体的压强均保持不变。

已知&和矗的内径均为出於的容积为％,水银的密度为Q,重力加速度大小为求：

田（a）

图⑹

（i）待测气体的压强；

（ii）该仪器能够测量的最人压强。

■5、…、“％gd芳/・・、“_兀咖干

【答杀】

（1）p=「（］八（“）Pg-———

AVQ+7td\l-h）4匕

【解析】（i）水银面上升至必的下端使玻璃泡中的气体恰好被封住，设此时被封闭的气体的体积为V,压强等于待测气体的压强6提升斤，直到金中水银面与K顶端等高时，血中的水银面比顶端低加设此时封闭气体的压强为P"体积为仏则

V=vo+

nd2l

片=^!

l②

4

由力学平衡条件得PLP+Pgh③

整个过程为等温过程，由玻意耳定律得pV=④

联立①②®④式得p=，严律八⑤

（ii）由题意知h

联立⑤⑥式有卩<泌上⑦

化

该仪器能够测量的最大压强为怯="咖十⑧

【名师点睛】此题主要考查玻意耳定律的应用，解题关键是确定以哪一部分气体为研究对象，并能找到气体在不同状态下的状态参量，然后列方程求解。

5.一个水平放置的汽缸，由两个截面积不同的圆筒连接而成。

活塞A、B用一长为4L的刚性细杆连接，L=0.5m,它们可以在筒内无摩擦地左右滑动。

A、B的截面积分别为Sa=40cm',Sb=20cm',A、B之间封闭着一定质量的理想气体，两活塞外侧（A的左方和B的右方）是压强为po=l.0X105Pa的人气。

当汽缸内气体温度为L=525K时两活塞静止于如图所示的位置。

4L

A

0

1求此时气体的压强

2现使汽缸内气体的温度缓慢下降，当温度降为多少时活塞A恰好移到两圆筒连接处

【答案】①Po②耳=300K

【解析】

试题分析：

（2）①以活塞整体为研究对象，分析受力知，几（s」

得：

戸=人

②对活塞受力分析，活塞向右缓慢移动过程中，气体发生等压变化

3Z-S<+ZSb_4LSs

由盖•吕萨克定律有：

石石

代入数值，得兀=300K时活塞a恰好移到两筒连接处。

考点：

气体压强的计算、盖一吕萨克定律。

【名师点睛】根据活塞受力情况，利用平衡条件计算内部气体的压强；根据等压变化遵从盖・吕萨克定律，利用此规律计算温度。

6.如图所示，长为31cm、内径均匀的细玻璃管开II向上竖直放置，管内水银柱的上端正好与管口齐平，封闭气体的长为10cm,温度为27°C,外界人气压强Po=75cniHg.若把玻璃管在竖直平面内缓慢转至开II竖直向下，然后再缓慢转回到开II竖直向上，求：

（1）开II竖直向下时空气柱的长度（已知960=16x60）

（2）玻璃管重新回到开口竖直向上时空气柱的长度：

（3）当开II再次向上后，管内气体温度升高到多少时，水银柱的上端恰好能重新与管口齐平（TR+273K）

【答案】

（1）16cm

（2）10.67cm（3）450K

【解析】

试题分析：

（1）设管的横截面积为S,对管内气体P严Po+2\cmHg=96cmHg,岭二10S

若开11向下时空气柱长度为h,

则^=^-（31-/7）,V2=Sh

由玻意耳定律有：

Py,=P2V2解得h二16cm

（2）开口向下时水银柱长度剩15cm,当开口再次向上时对管内气体

&=（75+⑸cmHg=90cmHg,V5=LS

由玻意耳定律有：

Py,=解得L二10.67cm

（3）对管内气体P4=P.=90cmHg,匕=（31—15）S=16S,7；=300K

yVc

由盖-吕萨克定律有：

解得7；=450K（或177°C）

T3X

考点：

玻意耳定律；盖-吕萨克定律

【名师点睛】本题考查气体实验定律和理想气体状态方程的综合应用，解决本题的关键时注意玻璃管转动过程中是否有水银溢出，正确列出初末各个状态参量代入方程即可求解.

7.如图1所示，左端封闭、内径相同的U形细玻璃管竖直放置，左管中封闭有长为L二20cm的空气柱，两管水银面相平，水银柱足够长。

已知大气压强为pcF75cmHgo

图1圈2

i.若将装置翻转180。

，使U形细玻璃管竖直倒置（水银未溢出），如图2所示。

当管中水银静止时，求左管中空气柱的长度；

ii.若将图1中的阀门S打开，缓慢流出部分水银，然后关闭阀门S,右管水银面下降了H二35cm,求左管水银面下降的高度。

【答案】i.20cm37.5cm,込.10cm

【解析】

试题分析：

i.设左管中空气柱的长度增加h,由玻意耳定律:

PoL=（p°—2h）（L+h）

代入数据解得：

力=°或/7=17.5cm

所以，左管中空气柱的长度为20cm或37.5如

ii.设左管水银面卞降的高度为x,左、右管水银面的高度差为y,

由几何关系：

x+y=H

由玻意耳定律：

以=（几一刃（厶“）

联立两式解得：

k+60x_700=°

解方程得：

x=10c〃7x=-10cm（舍去）故左管水银面下降的高度为

8.如图所示为''丄”型上端开II的玻璃管，管内有一部分水银封住密闭气体，上管足够长，图中粗细部分的截面积为S1=2S：

=2cm'、hLhE2cm。

封闭气体初始温度为

257°C,气体长度为L=22cm,外界大气压强PQ=76cmHg.求：

1若缓慢升高封闭气体温度，当所有水银全部压入细管内时封闭气体的压强：

2封闭气体温度至少升高到多少方可将所有水银全部压入细管内。

【答案】（l）U2cmHg

（2）

【解析】解：

①设所有水银全部压入细管内时水银柱的长度为H,封闭气体的压强为P,

则有：

h1sl+h2s2=Hs、

P=Po+pgH=H2cniHg

②气体初状态：

Pl=PQ+pg（hi+h2）=lOOcmHg

儿=S=22x2cm5=44mF,T严57°C十273K=330K

所有水银刚好全部压入细管内时：

P2=P=112cmHg,匕=（厶+九）耳=6&，屛

由理想气体状态方程知：

空=聲

7；T2

代入数据解得：

7；=571.2K

9.如图所示，光滑导热活塞C将体积为V。

的导热容器分成A、B两家，A、B中各封有一定质量的同种气体，A室左侧连接有一U形气压计（U形管内气体的体积忽略不计），B室右侧有一阀门K.可与外界人气相通，外界大气压等于76cmHg,气温恒定。

当光滑导热活塞C静止时，A、B两室容积相等，气压计水银柱高度差为38cm.现将阀门K打开,当活塞C不再移动时，求：

①A室的体积:

②B室从阀门K逸出的气体质量与原有质量的比

2

【答案】

（1）

（2）—

3

【解析】阀门K闭合，A室的体积为時丄V。

2

压强为巳二（76+38）cmH=U4cmHg

阀门K打开，A室的体积为Wa

压强为p'A=76cmHg（1分）

根据破耳定律得pNfp'卫a

解得V'尸

②阀门K打开后，若B室气体的质量不变，B室的体积为V’Vo

由于B室的气体逸出，留在B室的气体体积为V。

o75V-025V2

B室从阀门区选出的气体质量与原有质量的比为-0°=~

0.75%3

点睛：

本题考查气体定律的运用，解题关键是要分析好压强、体枳、温度三个参量的变化情况，选择合适的规律解决，难度不人，第②问解决的关键是要会利用状态相同的同种气体的质量比等于体积比.

10.内径相同、导热良好的“上”形细管竖直放置，管的水平部分左、右两端封闭，竖直管足够长且上端开II与人气相通，水银将水平管中的理想气体分为两部分，各部分长度如图所示。

现再向竖直管中缓慢注入水银，直到B中气柱长度变为4emo设外界温度不变，外界气压Po二76cmHgo求：

G）末态A中气柱长度；

（Ii）注入管中的水银柱的长度。

【答案】

（1）8cm

（2）25cm

【解析】设细管的横截面积为S

（i）对s中气体：

PbiS=pB2LH2s

对月中气体：

PA［LA1S=pA2LA2S

且：

Pai=Pbl»Pa2=Pb"厶趴=5cm,LB2=4cm,LAl=10cm联立各式得：

La严气出

Lfn

代入数据解得：

LA2=8cm

（ii）据题意：

］%=Po+〃竖］=76cmHg十12cmHg=88cmHg

将数据代入解得：

pB2=1lOcniHg

又：

Phi=l\+P竖2

P虽2=34cniHg

故注入水银柱的长度为：

L=Mem-12C/H+（L41-L42）+（LHl-Lb2）=25cm

【点睛】本题考查气体定律的综合运用，解题关键是要分析岀各部分气体的压强，然后运用玻意耳定律分析求解，关键注意列出初末状态参量，结合必要的几何知识求解.

11.一端开II的长直圆筒，在开II端放置一个传热性能良好的活塞，活塞与筒壁无摩擦且不漏气。

现将圆筒开II端竖直向卞缓慢地放入27°C的水中。

当筒底与水平面平齐时,恰好平衡，这时筒内空气柱长52cm,如图所示。

当水温缓慢升至87°C,试求稳定后筒底露出水面多少（不计筒壁及活塞的厚度，不计活塞的质量，圆筒的质量为M,水密度p水，大气压强Po）

婕m—

【答案】10・4纫7

【解析】设气体压强为P,活塞横截面积为S。

所以P=PQ+p^.gh①

以圆筒作为研究对彖，有PS-P°S=Mg②

连立①②两式，得

P水gS

可见，当温度发生变化时，液面高度保持不变，气体为等圧变化。

以气体作为研究对彖，设稳定后筒底露出水面的高度为x

Sx（52+x）

360

所以X=10.46777

点睛：

本题考查气体实验定律的应用，关键是正确分析封闭气体发生什么变化，确定初末状态参量，选择合适的规律列方程求解.

12・

（2）如图所示，粗细相同的导热玻璃A、B由橡皮软管连接，一定质量的空气被水银柱封闭在A管内，气柱长Li二39cm。

B管上方与大气相通，大气压强p尸76cmHg,坏境温度T。

二300K。

初始时两管水银面相平，若A管不动，将B管竖直向上缓慢移动一定高度后固定，A管内水银面上升了hLlcm。

大气压强不变。

求：

①B管与A管的水银面高度差；②要使两管内水银面再次相平，环境温度变为多少（结果取整数）

【答案】2cm；285K

【解析】①理想气体第1状态P：

二p。

VfL】STx=To第2状态pcVRLi-hJST：

=T0由理想气体状态方程Pi*二pM

解得P2=78cmHg

3管与A管的高度差为Ai=p：

~po•解得Ai二2cm.

②第3状态P3二poV3二（Lfi-丄Ai）ST3

2

由理想气体状态方畤=解得T3=285K

点睛：

本题考查气体实验定律和理想气体状态方程的应用，关键是确定气体的各个状态参量，确定状态的变化过程，同时运用一定的几何知识即可求解；

13.如图甲所示，有一“上”形、粗细均匀的玻璃管，开II端竖直向上放置，水平管的两端封闭有理想气体A与B,气柱长度都是22cm,中间水银柱总长为12cm.现将水银全部推进水平管后封闭管道接II处，并把水平管转成竖直方向，如图乙所示，为了使A、B两部分气体一样长，把B气体的一端单独放进恒温热水中加热，试问热水的温度应控制为多少（己知外界人气压强为76cmHg,气温275K.）

22cm4cm4cm--

【答案】.

【解析】玻璃管开II向上时，AB两部分气体的初状态

PA=PB=SQcmHg,LA=LB=22cm9T=275K将水银全部推进水平管时PAl=P亦—=S=20伽

对A气体，由玻意耳定律：

PALA=PAiLAl,解得PM=SScmHg

对于最终状态的3气体PH2=乙汁12cmHg=lOOcmHg

PLPL

由理想气体状态方程皿=隹如解得热水的温度7；=312.5K.

14.如图所示，竖直玻璃管粗细均匀，上端开「1,下端封闭有长度LHOcm的理想气体,中间水银柱长h二24cm。

在竖直管中间接一水平玻璃管，右端开I】于大气相通，管的直径与竖直部分相同，用光滑活塞封闭足够长的水银柱，已知外界人气压强po=76cmHg,保持环境温度恒为TF300K,现用外力缓慢向左推活塞，使下端气柱长变为L-25cm,求:

1气柱长度为L2二25cm时，活塞移动的距离d：

2若活塞左移①中的距离d后固定，对玻璃管缓慢加热，使下端气柱长又变回L”求此时封闭气体的温度T2.

【答案】

（1）20cm

（2）360K

【解析】①设玻璃管的横截面枳为S,气柱长为厶时竖直玻璃管中水银柱的长度为”，在活塞向左移动的过程中，封闭气体做等温变化，有：

（Po+恣町厶S=（+pgH）—S

又d=h—h',解得d=20cm

②该过程中封闭气体做等压变化，有竽=羊，

人‘2

解得T2=360/C

15.如图甲所示，粗细均匀、横截面积为S的导热光滑足够长的细玻璃管竖直放置，管内用质量为加的水银柱密封着长为Z的理想气柱。

已知环境温度为7；,大气压强为咒，重力加速度为S

乙

（i）若仅将环境温度降为辛，求稳定后的气柱长度；

（ii）若环境温度7；不变，将玻璃管放于水平桌面上并让其以加速度＜2向左做匀加速直线运动（如图乙所示），求稳定后的气柱长度。

■i宀■/f、2L，c、Mg十PoS儿

【口案】（l）§

（2）~poS-n-B

LS_hS

【解析】（i）当气体温度变化时，其压强不变，根据盖-吕萨克定律，有：

頁二乎，解

2

得h=§L

（ii）当玻璃管竖直时，气体压强为p］二po+詈当玻璃管水平运动时，对水银柱有:

P2S-P0S=ma

对气体有：

piLS=p：

xS

联立解得：

X

（itg十pcS）L

PoS-ma

点睛：

此题考查了求气体的温度、空气柱的长度，分析清楚气体的状态变化过程、求出气体的状态参量是解题的前提与关键，应用盖吕萨克定律与玻意耳定律可以解题.