第5章 动态回归与误差修正模型案例.docx

第5章 动态回归与误差修正模型案例.docx

《第5章 动态回归与误差修正模型案例.docx》由会员分享，可在线阅读，更多相关《第5章 动态回归与误差修正模型案例.docx（12页珍藏版）》请在冰豆网上搜索。

第5章动态回归与误差修正模型案例

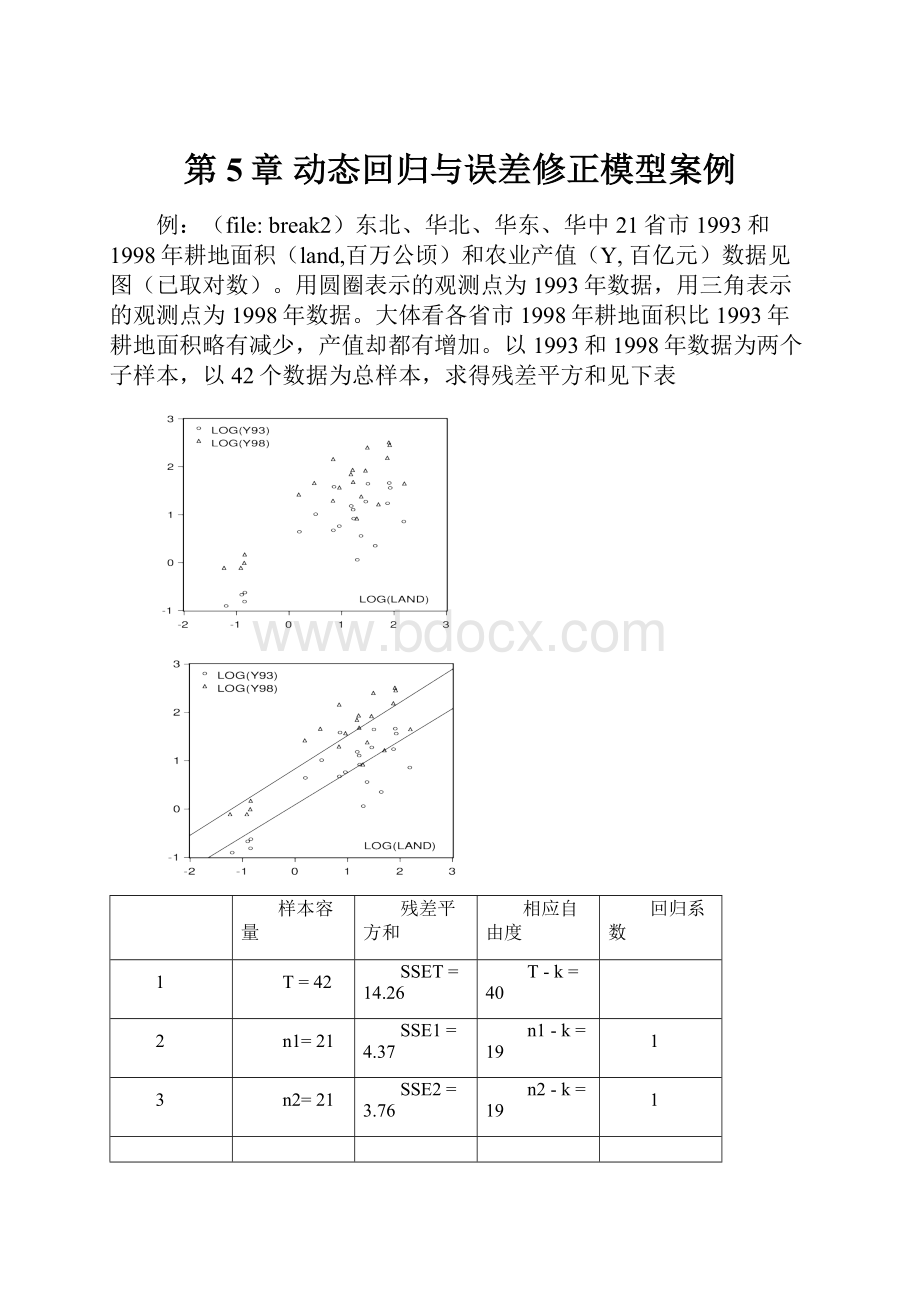
例：

（file:

break2）东北、华北、华东、华中21省市1993和1998年耕地面积（land,百万公顷）和农业产值（Y,百亿元）数据见图（已取对数）。

用圆圈表示的观测点为1993年数据，用三角表示的观测点为1998年数据。

大体看各省市1998年耕地面积比1993年耕地面积略有减少，产值却都有增加。

以1993和1998年数据为两个子样本，以42个数据为总样本，求得残差平方和见下表

样本容量

残差平方和

相应自由度

回归系数

1

T=42

SSET=14.26

T-k=40

2

n1=21

SSE1=4.37

n1-k=19

1

3

n2=21

SSE2=3.76

n2-k=19

1

注：

三次回归的模型形式Lnoutt=0+1Lnlandt+ut。

因为，

F=

=

=14.33>F（1,40）=7.31

所以两个年度21省市的农业生产发生了很大变化。

案例1：

开滦煤矿利润影响因素的实证分析（1903-1940，动态分布滞后模型，file:

LH1）

（发表在《学术论坛》，2003.1,p.88-90）

图1开滦煤矿销煤量变化曲线（x1,1903-1940）

图2开滦煤矿吨煤售价变化曲线（x2,1903-1940）

图3开滦煤矿利润变化曲线（1903-1940）

图4开滦煤矿利润对销煤量散点图

图5开滦煤矿利润对吨煤售价散点图

1）建立ADL（2,2,2）

Yt=0.2937Yt-1+0.2038Yt-2+4.2469X1t–3.5106X1t-1

（2.5）（2.4）（7.3）（-5.5）

+2964.25X2t–1390.66X2t–1-1433.01X2t–2

（1）

（7.3）（-1.7）（-2.3）

R2=0.96,s.e.=1504.7,LM

（2）=4.10,DW=2.16,F=128.7,Q（15）=8.1（1905-1940）

用上式求长期关系，

Yt=1.4653X1t+278.6X2t

（2）

j=1,2

1*=1.4653（1453.8/7134.1）=0.2986

2*=278.6（2.2067/7134.1）=0.0862

无量纲长期参数估计结果是

Y=0.2986X1+0.0862X2（3）

这说明实际上X1对Y的影响大于X2对Y的影响。

2）ADL（1,1,2）

LnYt=0.7502LnYt-1+1.8804LnX1t–1.6210LnX1t-1

（9.0）（8.2）（-6.7）

+1.5037LnX2t–1.4787LnX2t–1（4）

（6.0）（-4.9）

R2=0.95,LM

（2）=1.91,DW=1.7,F=140.7,Q（15）=6.0,（1903-1940）

LnYt=1.038LnX1t+0.100LnX2t（5）

这说明LnYt对LnX1t的弹性系数远远大于LnYt对LnX2t的弹性。

案例2：

关于日本人均消费的误差修正模型（见教材206-213页，file:

b5c1）

本案例采用“一般到特殊”建模方法用1963-1993年（T=31）日本人均年消费、可支配收入（单位：

万日元）和价格数据建立消费模型。

（注意：

本章假定变量具有平稳性。

但本案例中变量是非平稳的。

因为变量具有协整性，所以不影响对误差修正模型的介绍。

）

1）定义变量如下：

LnCt：

对数的人均年消费额

（不变价格，1985=1）。

LnIt：

对数的人均年可支配收入额

（不变价格，1985=1）。

LnPt：

对数的消费价格指数（1985=1）。

原始数据摘自日本《家计调查年报》1963,…,1993（日本总务厅统计局出版）经作者进一步计算得到LnCt，LnIt和LnPt数据（见表5.1）。

曲线分别见图5.2和图5.3。

图5.2LnCt和LnIt

图5.3LnPt

2）建立一般模型

首先建立一个ADL（1,1,2）模型（含有两个外生变量，解释变量与被解释变量各滞后一期）作为“一般模型”。

用1963-1993年数据得估计结果

=0.2621+0.8297LnIt-0.0414LnPt

（1.81）（7.75）（-0.65）

+0.6501LnCt-1-0.5532LnIt-1+0.0543LnPt-1

（4.69）（-3.65）（1.07）

R2=0.9989,SSE=0.0015,DW=1.90（5.87）

LM1=0.039,LM2=4.76,ARCH=0.58,T=30

其中括号内给出的数字是t值。

LM1和LM2分别用来检验

是否存在一阶和二阶自相关。

ARCH用来检验

是否存在异方差。

因为2

（1）=3.84，2

（2）=5.99，DW=1.90，可见模型（5.87）的残差项中不存在自相关和异方差。

因为R2=0.9989，（5.87）式中的解释变量解释了LnCt变化的99.89%。

综上，可以把（5.87）式看作“一般模型”。

3）长期关系

用（5.87）式计算变量间的长期关系。

*=

=0.2621/（1-0.6501）=0.7491,

*=

=（0.8297-0.5532）/（1-0.6501）

=0.7902,

*=

=（-0.0414+0.0543）/（1-0.6501）

=0.0369.

长期关系

LnCt=0.7491+0.7902LnIt+0.0369LnPt（5.89）

4）简化模型

从（5.87）式中删除解释变量LnPt得

=0.3181+0.8756LnIt+0.6466LnCt-1

（2.75）（10.97）（4.72）

-0.6078LnIt-1+0.0218LnPt-1.（5.91）

（-4.86）（2.09）

R2=0.9989,SSE=0.0015,DW=1.95

LM2=2.8,ARCH=0.26,F=68.1,T=30

由DW，LM2和ARCH的值知上式既不存在自相关也不存在异方差（由一般到特殊的第一步）。

解释变量解释了LnCt变化的99.89%。

由t值可以看出上式中的所有参数都具有显著性，不应该再从中删除任何解释变量。

5）试分析

假如从上式中删除收入变量（LnIt和LnIt-1），得

=0.1932+0.9600LnCt-1-0.0168LnPt-1.（5.92）

（0.88）（19.95）（-0.78）

R2=0.9935,SSE=0.0088,

DW=2.27,F=2060.3,T=30

这相当于对模型（5.90）施加约束0=1=0。

对上述联合约束进行检验的F统计量的值按下式计算，

=

=60.8（5.93）

因为F0.05（2,25）=3.39，F=60.83.39，约束条件0=1=0被拒绝，所以LnIt和LnIt-1是重要的解释变量，不应从模型中删除。

同理LnCt-1和LnPt-1也是重要的解释变量，不应从模型中删除。

6）建立误差修正模型

（1）从模型（5.91）两侧同减LnCt-1，重新估计得

=0.3181+0.8756LnIt-0.3534LnCt-1

（2.75）（10.97）（-2.58）

-0.6078LnIt-1+0.0218LnPt-1,（5.95）

（-4.86）（2.09）

R2=0.9159,SSE=0.0015,DW=1.95,

F=68.1,T=30.

（2）在（5.95）式右侧同时加减LnIt-1，重新估计得，

=0.3181+0.8756LnIt-0.3534LnCt-1

（2.75）（10.97）（-2.58）

+0.2678LnIt-1+0.0218LnPt-1,（5.97）

（2.35）（2.09）

R2=0.9159,SSE=0.0015,DW=1.95,

LM2=2.8,ARCH=0.26,F=68.1,T=30.

（3）整理模型

对上式作进一步线性变换，得到误差修正模型的标准形式。

=0.3181+0.8756LnIt

-0.3534（LnCt-1-0.7578LnIt-1-0.0617LnPt-1）,（5.98）

把截距项移入括号，

=0.8756LnIt

-0.3534（LnCt-1-0.9001-0.7578LnIt-1-0.0617LnPt-1）

（5.99）

日本（对数）人均消费与人均可支配收入、价格的长期关系是

LnCt=0.9001+0.7578LnIt+0.0617LnPt

（5.100）

这一结果与（5.89）式

LnCt=0.7491+0.7902LnIt+0.0369LnPt

（5.89）

极为相似。

（5.99）式中误差修正项的系数为负。

这个结果与误差修正机制相一致。

-0.3534说明误差修正项以35.34%的比例对下一年度的LnCt的取值产生影响。

LnIt的短期参数是0.8756。

误差修正模型（5.99），即模型（5.97）的残差图以及LnCt的实际曲线与拟合曲线见图5.4。

图5.4LnCt的实际值与拟合值以及残差序列

图5.5LnCt的实际值与拟合值以及残差序列

（相对于误差修正模型（5.99））（相对于误差修正模型（5.102））

由上可知（5.87）式是“一般模型”，（5.99）式是最后的“特殊模型”。

估计的长短期参数都通过了显著性检验，残差序列中不存在自相关。

4）直接建模

现在用LnCt，LnIt和LnPt直接建立模型如下，

=0.6071+0.8185LnIt+0.0337LnPt（5.102）

（5.09）（33.15）（2.68）

R2=0.9979,SSE=0.0035,

DW=0.64,F=6552.4,T=31.

虽然回归系数都通过了t检验，但检验自相关的DW值却非常小。

由DW=0.64知自相关系数=1–DW/2=1-0.32=0.68。

说明残差序列中存在严重的自相关。

模型（5.87）和（5.102）的SSE分别是0.0015和0.0035。

可见模型（5.102）对数据的拟合远不如模型（5.87）好，即不如模型（5.99）好。

模型（5.102）的残差图以及LnCt的实际曲线与拟合曲线见图5.5，该图说明模型不但存在严重的自相关，而且预测精度也不高。

实际上（5.102）式是一个虚假回归式（检验方法见第7章）。