IIR数字滤波器实现.docx

IIR数字滤波器实现.docx

《IIR数字滤波器实现.docx》由会员分享，可在线阅读，更多相关《IIR数字滤波器实现.docx（12页珍藏版）》请在冰豆网上搜索。

IIR数字滤波器实现

IIR数字滤波器实现（mantlab+C语言）

题目：

16k采样率音频数据下采样到8k采样率

求解方案分析：

直接每隔一个取一个采样值，这样就可以得到8k采样率的数据。

但是这样明显会有问题。

按照采样率变换理论，首先应该通过一个低通滤波器，滤掉[pi/2,pi]这个区间上的频率，以防止下采样造成的频率混叠。

这个低通滤波器在很多书上都用FIR滤波去实现，并且可以用FIR滤波的多相结构去实现。

这样滤波和下采样过程可以互换位置。

即先下采样再进行多相FIR滤波。

在嵌入式设备上FIR滤波会占用较长的时间，为此，我们可以采用IIR滤波器来做。

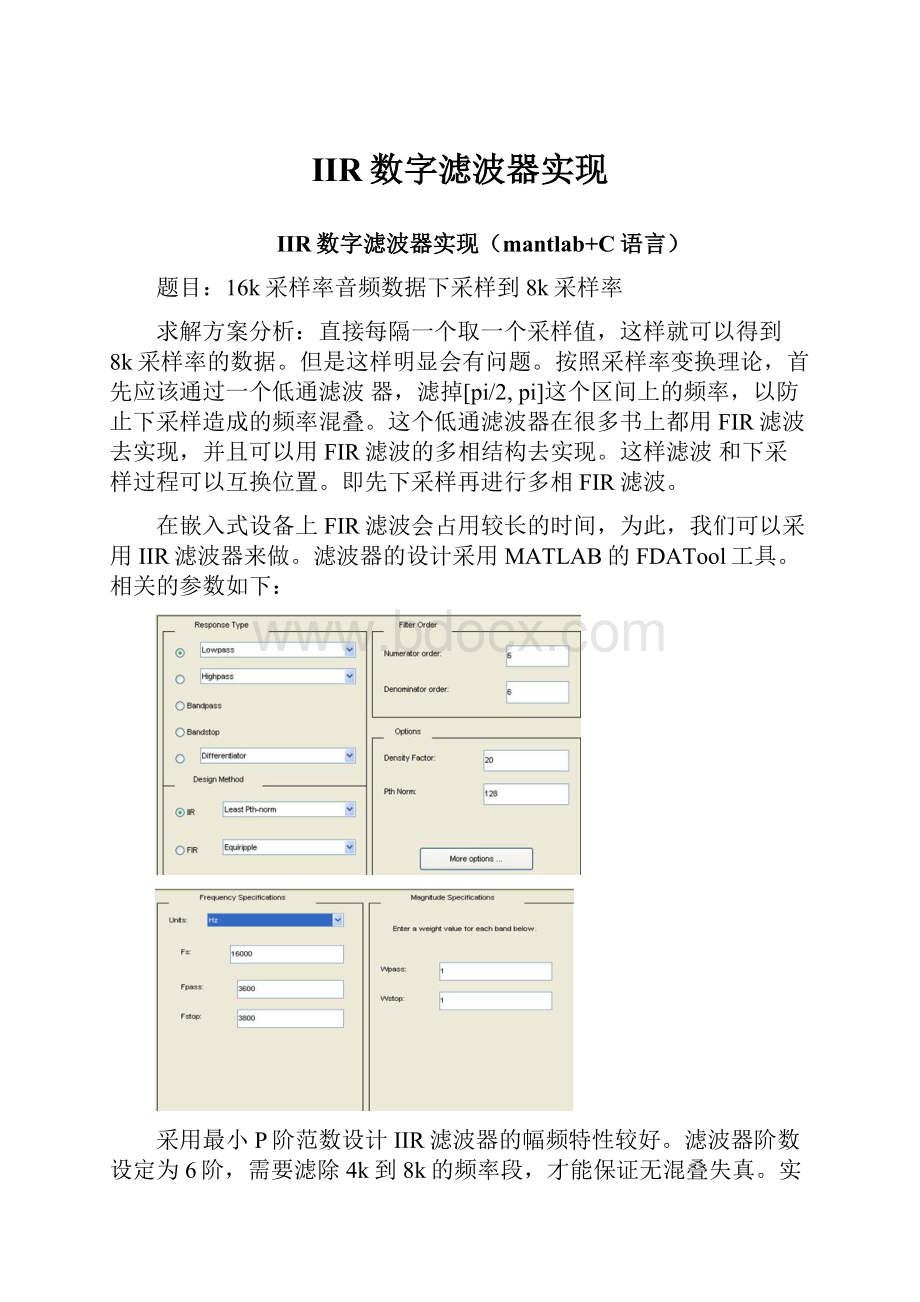
滤波器的设计采用MATLAB的FDATool工具。

相关的参数如下：

采用最小P阶范数设计IIR滤波器的幅频特性较好。

滤波器阶数设定为6阶，需要滤除4k到8k的频率段，才能保证无混叠失真。

实际由于滤波器的特性没法做到理想的状态，选择滤波器截止频率为3800hz，3600到3800为过渡带宽。

其它选项采用默认设置。

设计的滤波器幅度响应如下图：

生成的滤波器系数文件如下：

/*

 *FilterCoefficients（CSource）generatedbytheFilterDesignandAnalysisTool

 *

 *GeneratedbyMATLAB（R）7.6andtheSignalProcessingToolbox6.9.

 *

 *Generatedon:

03-Dec-201010:

41:

03

 *

 */

/*

 *Discrete-TimeIIRFilter（real）

 *-------------------------------

 *FilterStructure    :

Direct-FormII,Second-OrderSections

 *NumberofSections  :

3

 *Stable              :

Yes

 *LinearPhase        :

No

 */

/*GeneraltypeconversionforMATLABgeneratedC-code  */

#include "tmwtypes.h"

/*

 *Expectedpathtotmwtypes.h

 *D:

/MATLAB/R2008a/extern/include/tmwtypes.h

 */

#define MWSPT_NSEC 7

const int NL[MWSPT_NSEC]={1,3,1,3,1,3,1};

const real64_T NUM[MWSPT_NSEC][3]={

  {

    0.09065504059673,                 0,                 0

  },

  {

                   1,  -0.132********53,   0.9999674089086

  },

  {

                   1,                 0,                 0

  },

  {

                   1,   0.1670351201308,   0.9999889247428

  },

  {

                   1,                 0,                 0

  },

  {

                   1,    1.417032671609,   0.9978019623105

  },

  {

                   1,                 0,                 0

  }

};

const int DL[MWSPT_NSEC]={1,3,1,3,1,3,1};

const real64_T DEN[MWSPT_NSEC][3]={

  {

                   1,                 0,                 0

  },

  {

                   1,    -0.40321085647,   0.7334254033056

  },

  {

                   1,                 0,                 0

  },

  {

                   1,  -0.6868636040216,   0.2670185171768

  },

  {

                   1,                 0,                 0

  },

  {

                   1,  -0.2880720042256,   0.9480010462991

  },

  {

                   1,                 0,                 0

  }

};

上述系数是3个2阶节IIR结构的级联。

可以转换为我们熟悉的b/a的形式如下：

double a[3][3]={

     {1,  -0.6868636040216,   0.2670185171768},

     {1,    -0.40321085647,   0.7334254033056},

     {1,  -0.2880720042256,   0.9480010462991}

};

double b[3][3]={

     {1,   1.417032671609,   0.9978019623105},

     {1,   0.1670351201308,   0.9999889247428},

     {1,  -0.1323122149853,   0.9999674089086},

};

注意上面系数文件中还有一个增益：

double.0906********；

这个增益最好在第一级实现以后加入运算。

这样可以减小误差，保证数据动态范围不被溢出。

尤其是在定点计算的时候尤为如此。

2阶节IIR滤波的直接实现

一个2阶节结构是下面这样一个表达式：

 实现上面这个表达式需要4个过去的历史值，把它定义在结构体

typedef struct tag_IIR_State_2order

{

     float y2;

     float y1;

     float x1;

     float x0;

} IIR_State_2order;

调用下面函数之前需要把上述结构体所有值初始化为零。

滤波按一帧一帧数据进行。

#define  ONE_FRAME_SAMPLE_SIZE   1024

void cy_signal_filter_by_iir（signed short* pcmIn, IIR_State_2order* filter_state, float a[], float b[], signed short*pcmOut）

{

   int i;

   float x2;

   float tmp;

   for （ i =0; i < ONE_FRAME_SAMPLE_SIZE; i++）

   {

      x2 = filter_state->x1;

      filter_state->x1 = filter_state->x0;

      filter_state->x0 = pcmIn[i];

      tmp =（ float ）（b[0]* filter_state->x0 + b[1]* filter_state->x1 +

b[2]* x2 - a[1]* filter_state->y1 - a[2]* filter_state->y2）;

       if（tmp >=32767）

       {

           tmp =32767;

       }

       if（tmp <=-32768）

       {

          tmp =-32768;

       }

      pcmOut[i]=（signed short）tmp;

      filter_state->y2 = filter_state->y1;

      filter_state->y1 = tmp;

   }

}

有一个简单的技巧可以把上面的计算简化，使得历史状态数由4减少为2。

定义下面的表达式：

结构体定义如下：

typedef struct tag_IIR_State_2order

{

     float st1;

     float st2;

} IIR_State_2order;

void cy_signal_filter_by_iir（signed short* pcmIn, IIR_State_2order* filter_state, float a[], float b[], signed short*pcmOut）

{

   int i;

   float st;

   float Tmp_fl;

   for （ i =0; i < ONE_FRAME_SAMPLE_SIZE; i++）

   {

        st =（float）（pcmIn[i]-  a[1]* filter_state->st1  - a[2]* filter_state-> st2）;

        Tmp_fl = b[0]*  st + b[1]* filter_state->st1 + b[2]* filter_state->st2;

        filter_state->st2= filter_state->st1;

        filter_state->st1 = st;

        if（Tmp_fl >=32767.0）

        {

            Tmp_fl =32767;

        }

        if（Tmp_fl <=-32768）

        {

           Tmp_fl =-32768;

        }

         pcmOut[i]=（signed short）Tmp_fl;

   }

}

6阶节IIR滤波的实现

有个上面的基础，我们来实现上面设计的6阶IIR滤波器。

6阶节分解为3个2阶节级联实现。

每个2阶节需要2个历史状态，总共需要6个历史状态。

结构体定义如下：

typedef struct tag_IIR_State_3Order

{

     double w01;

     double w02;

     double w11;

     double w12;

     double w21;

     double w22;

}IIR_State_6order;

代码中数组a,b,还有gain的定义见第一部分。

void cy_signal_filter_by_6th_iir（signed short* pcmIn, IIR_State_6order* filter_state, int sample_size）

{

     double x1, x2, x3, Tmp_f00, Tmp_f10, Tmp_f20;

     int i;

     double Tmp_pcm;

     for （i =0; i < sample_size; i++）

     {

         Tmp_pcm = pcmIn[i];

         Tmp_f00 = Tmp_pcm - a[0][1]* filter_state->w01 - a[0][2]* filter_state->w02;

         x1 = Tmp_f00 + b[0][1]* filter_state->w01 + b[0][2]* filter_state->w02;

         filter_state->w02 = filter_state->w01;

         filter_state->w01 = Tmp_f00;

          x1 = gain * x1;

          Tmp_f10 = x1 - a[1][1]* filter_state->w11 - a[1][2]* filter_state->w12;

         x2 = Tmp_f10 + b[1][1]* filter_state->w11 + b[1][2]* filter_state->w12;

         filter_state->w12 = filter_state->w11;

         filter_state->w11 = Tmp_f10;

          Tmp_f20 = x2 - a[2][1]* filter_state->w21 - a[2][2]* filter_state->w22;

         x3 = Tmp_f20 * b[2][0]+ b[2][1]* filter_state->w21 + b[2][2]* filter_state->w22;

         filter_state->w22 = filter_state->w21;

         filter_state->w21 = Tmp_f20;

         if （x3 >=32767）

         {

              x3 =32767;

         }

         if （x3 <=-32768）

         {

              x3 =-32768;

         }

         pcmIn[i]=（signed short）x3;

     }

}

 最后看下滤波的效果：

滤波之后的频谱：

滤波效果不错，下面可以进行下采样了。