相似三角形经典模型总结及例题分类.docx

相似三角形经典模型总结及例题分类.docx

《相似三角形经典模型总结及例题分类.docx》由会员分享，可在线阅读，更多相关《相似三角形经典模型总结及例题分类.docx（13页珍藏版）》请在冰豆网上搜索。

相似三角形经典模型总结及例题分类

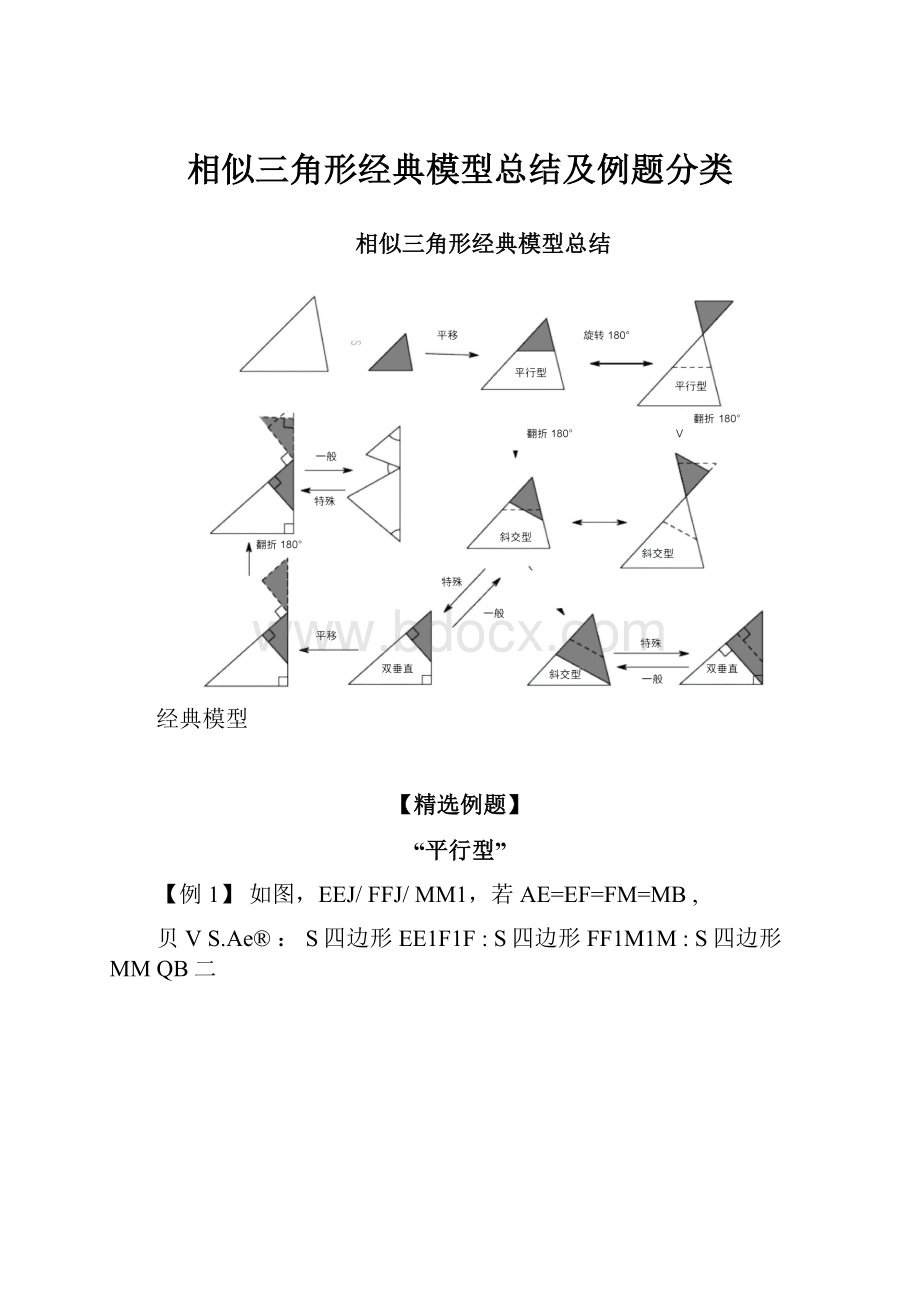
相似三角形经典模型总结

经典模型

【精选例题】

“平行型”

【例1】如图，EEJ/FFJ/MM1，若AE=EF=FM=MB,

贝VS.Ae®：

S四边形EE1F1F:

S四边形FF1M1M:

S四边形MMQB二

［例2】如图，AD//EFM/NBC若AD=9,BC=18,AE:

EM:

MB=2:

3:

4,则

EF=,MN=

长线，AB的延长线分别相交于点E，F，G，H

求证：

PEPH

PF一PG

【例引

11

已知：

在ABC中，ADAB，延长BC到F,使CFBC,连接FD交AC于点E

23

【例6】已知：

D,E为三角形ABC中AB、BC边上的点，连接DE并延长交AC的延长线于点F,

BD:

DE二AB:

AC

求证：

:

CEF为等腰三角形

【例7】如图，已知AB//EF//CD，若AB=a，CD=b，EF=c，求证：

1=——

cab

【例8】如图，找出S.abd、Sbed、S.BCD之间的关系，并证明你的结论

【例9】如图，四边形ABCD中，B=/D=90，M是AC上一点，ME_AD于点E,MF_BC

于占

J八、、

F

求证:

MFME,

1

ABCD

C

【例10】如图，在ABC中，D是AC边的中点，过D作直线EF交AB于E,交BC的延长线于F

求证：

AEBF二BECF

【例11】如图，在线段AB上，取一点C，以AC，CB为底在AB同侧作两个顶角相等的等腰三角形

ADC和CEB，AE交CD于点P，BD交CE于点Q,

求证：

CP=CQ

【例12】阅读并解答问题.

在给定的锐角三角形ABC中，求作一个正方形DEFG，使D，E落在BC边上，F,G分别落在AC,AB边上，作法如下：

第一步：

画一个有三个顶点落在ABC两边上的正方形D'E'F'G'如图，

第二步：

连接BF'并延长交AC于点F

第三步：

过F点作FE_BC,垂足为点E第四步：

过F点作FG//BC交AB于点G第五步：

过G点作GD_BC，垂足为点D四边形DEFG即为所求作的正方形

问题：

⑴证明上述所作的四边形DEFG为正方形

⑵在ABC中，如果BC=6「3,ABC=45,•BAC=75,求上述正方形DEFG的边长

“平行旋转型”

图形梳理:

C,E',F'共线

①证明：

AD2BC2二AB2CD2

【例14】当MOD，以点O为旋转中心，逆时针旋转日度（0£日＜90），问上面的结论是否成立，请说明理由

D

【例15】（全国初中数学联赛武汉选拔赛试题）如图，四边形

AG:

DF:

CE=.

“斜交型”

【例16】如图，.:

ABC中，D在AB上，且DE//BC交AC于E,F在AD上，且AD^AFAB,求证：

AEFLACD

【例17】如图，等边三角形ABC中，D,E分别在BC,AB上，且CE二BE,AD,CE相交于M,求证：

EAMLECA

【例18】如图，四边形ABCD的对角线相交于点O,.BAC—CDB,求证：

.DAC=.CBD

ABBCCA

【例佃】如图，设伴二CA，则.仁.2吗?

ADDEEA

等于18和2，DE=2，求AC边上的高

BD1

【例21】如图，在等边ABC的边BC上取点D，使，作CH_AD，H为垂足，连结BH。

CD2

求证：

DBH"DAB

【例22】已知：

在正三角形ABC中，点D、E分别是AB、BC延长线上的点，且BD=CE,直线CD与AE相交于点F

2

求证：

①DC=AE,②AD=DCDF

“斜交特殊型”（隐含三垂直）

【例23】已知，如图，.ABC中，AD_BC于点D，DE_AC于点E，DF_AB于点F，求证:

.AEF—B

丄AP,垂足为G交CE于D,求证：

CE2=PEDE。

【例26】如图，已知：

正方形ABCD中，点M、N分别在AB、BC上，且BM二BN,BP_MC

于点P

求证：

DP_NP

【例27】如图，Rt也ABC中，NBAC=90°，AB=AC=2,点D在BC上运动（不经过B,C），过点D作ADE=45,DE交AC于E

1图中有无与ABD一定相似的三角形，若有，请指出来并加以证明

2设BD二x，AE二y，求y与x的函数关系，并写出其定义域；

3若ADE恰为等腰三角形，求AE的长