等腰三角形与尺规作图中考题练习题及答案解析.docx

等腰三角形与尺规作图中考题练习题及答案解析.docx

《等腰三角形与尺规作图中考题练习题及答案解析.docx》由会员分享，可在线阅读，更多相关《等腰三角形与尺规作图中考题练习题及答案解析.docx（29页珍藏版）》请在冰豆网上搜索。

等腰三角形与尺规作图中考题练习题及答案解析

等腰三角形与尺规作图

一．选择题（共5小题）

1．（盐城）若等腰三角形的顶角为40°，则它的底角度数为（　　）

A．

40°

B．

50°

C．

60°

D．

70°

2．（2014•日照）已知△ABC的周长为13，且各边长均为整数，那么这样的等腰△ABC有（　　）

A．

5个

B．

4个

C．

3个

D．

2个

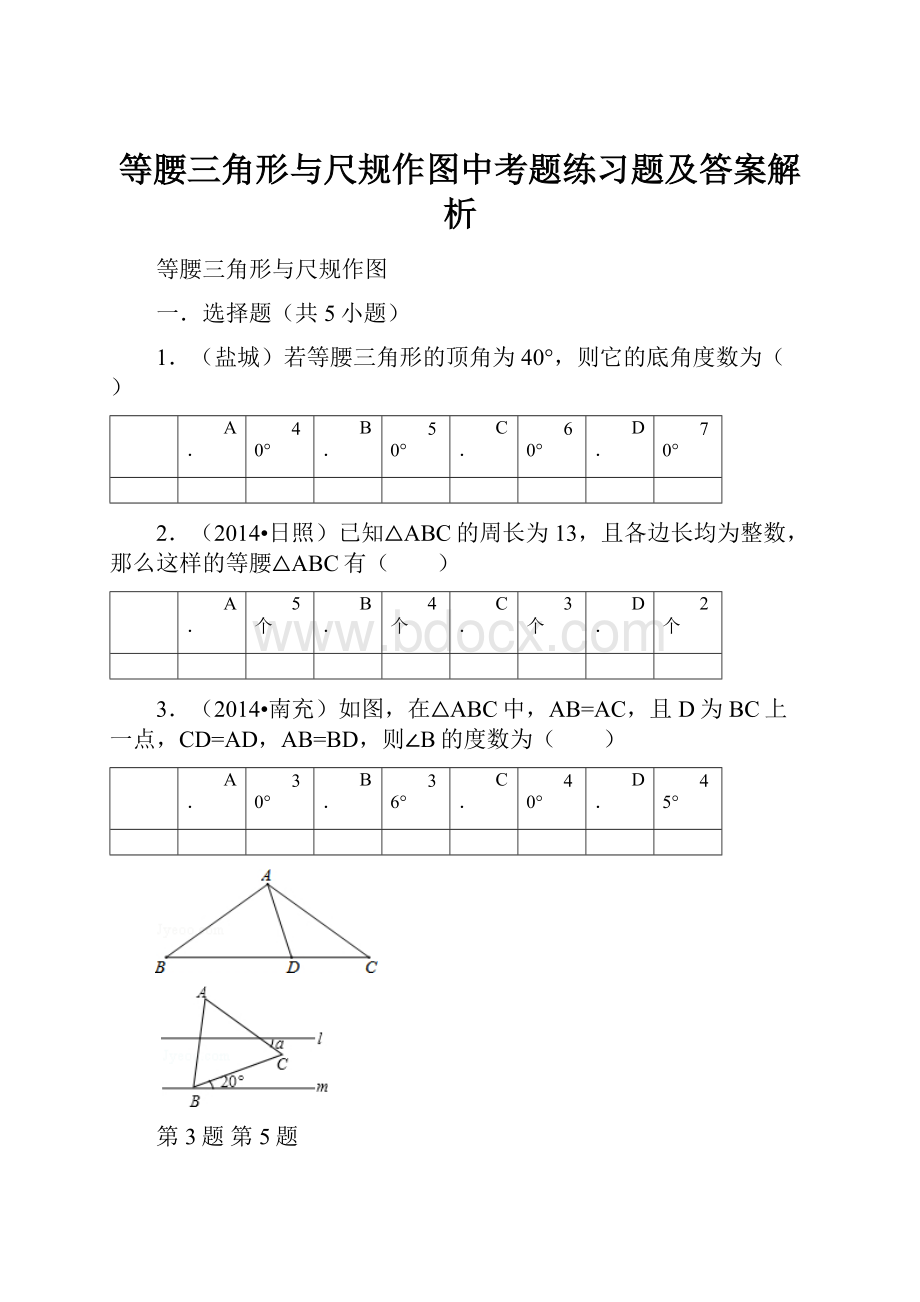
3．（2014•南充）如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）

A．

30°

B．

36°

C．

40°

D．

45°

第3题第5题

4．（宜城市模拟）若等腰三角形一腰上的高和另一腰的夹角为25°，则该三角形的一个底角为（　　）

A．

32.5°

B．

57.5°

C．

32.5°或57.5°

D．

65°或57.5°

5．（路南区一模）已知：

如图，l∥m，等边△ABC的顶点B在直线m上，边BC与直线m所夹锐角为20°，则∠α的度数为（　　）

A．

60°

B．

45°

C．

40°

D．

30°

二．填空题（共5小题）

6．（丽水）如图，在△ABC中，AB=AC，AD⊥BC于点D，若AB=6，CD=4，则△ABC的周长是　_________　．

第6题第8题

7．（澄海区模拟）已知实数x，y满足|x﹣4|+

=0，则以x，y的值为两边长的等腰三角形的周长是　_________　．

8．（晋江市质检）如图，在等腰△ABC中，AB=AC，AD⊥BC，若∠BAD=20°，则∠BAC=　_________　度．

9．（潜江模拟）已知等腰三角形有一个角是50°，则它的另外两个角是　_________　．

10．（南安市一模）若等腰三角形两边长分别为10和5，则它的周长是　_________　．

三．解答题（共11小题）

11．（淄博）如图，AD∥BC，BD平分∠ABC．求证：

AB=AD．

12．（珠海）如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．

（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）

（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）

13．（葫芦岛二模）已知如图，A（3，0），B（0，4），C为x轴上一点．

（1）画出等腰三角形ABC；

（2）求出C点的坐标．

14．（温州模拟）在下列四个条件中：

①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE．请选出两个作为条件，得出△AED是等腰三角形（写出一个即可），并加以证明．已知：

　_________　；

求证：

△AED是等腰三角形．

15．（昌平区一模）如图，已知△ABC和△ADE都是等边三角形，连接CD、BE．求证：

CD=BE．

16．（白云区模拟）如图，△ABC中，BC∥AM，D是CA延长线上的一点，且∠B=∠DAM．

求证：

△ABC是等腰三角形．

17．（香洲区一模）△ABC是等腰三角形，AB=AC，∠A=36°．

（1）利用尺规作B的角平分线BD，交AC于点D；（保留作图痕迹，不写作法）

（2）判断△DBC是否为等腰三角形，并说明理由．

18．（珠海）如图，在Rt△ABC中，∠ACB=90°．

（1）用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）

（2）连接AP，当∠B为　_________　度时，AP平分∠CAB．

19．（锦州）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．

（1）利用尺规作图在AC边上找一点D，使点D到AB、BC的距离相等．（不写作法，保留作图痕迹）

（2）在网格中，△ABC的下方，直接画出△EBC，使△EBC与△ABC全等．

20．如图，河边有ab两个村庄，现要在河边建一抽水站，铺设管道抽水到a村和b村，要使所用管道最少，应如何选择抽水站的地址？

通过尺规作图找出符合条件的抽水站位置，并说明理由。

21．作图与证明按下列要求尺规作图（保留作图痕迹）：

如图，已知∠ABC，在边AB上有一点D，请过点D用尺规作出与BC平行的一条直线，并将你的理由填写在横线上．理由：

　_________　．

参考答案与试题解析

一．选择题（共5小题）

1．（盐城）若等腰三角形的顶角为40°，则它的底角度数为（　　）

A．

40°

B．

50°

C．

60°

D．

70°

考点：

等腰三角形的性质．菁优网版权所有

专题：

计算题．

分析：

根据等腰三角形的性质和三角形内角和定理可直接求出其底角的度数．

解答：

解：

因为等腰三角形的两个底角相等，

又因为顶角是40°，

所以其底角为

=70°．

故选：

D．

点评：

此题考查学生对等腰三角形的性质的理解和掌握，解答此题的关键是知道等腰三角形的两个底角相等．

2．（日照）已知△ABC的周长为13，且各边长均为整数，那么这样的等腰△ABC有（　　）

A．

5个

B．

4个

C．

3个

D．

2个

考点：

等腰三角形的性质；三角形三边关系．菁优网版权所有

分析：

由已知条件，根据三角形三边的关系，任意两边之和大于第三边，任意两边之差小于第三边，结合边长是整数进行分析．

解答：

解：

周长为13，边长为整数的等腰三角形的边长只能为：

3，5，5；或4，4，5；或6，6，1，共3个．

故选：

C．

点评：

本题考查了等腰三角形的判定；所构成的等腰三角形的三边必须满足任意两边之和大于第三边，任意两边之差小于第三边．解答本题时要进行多次的尝试验证．

3．（南充）如图，在△ABC中，AB=AC，且D为BC上一点，CD=AD，AB=BD，则∠B的度数为（　　）

A．

30°

B．

36°

C．

40°

D．

45°

考点：

等腰三角形的性质．菁优网版权所有

分析：

求出∠BAD=2∠CAD=2∠B=2∠C的关系，利用三角形的内角和是180°，求∠B，

解答：

解：

∵AB=AC，

∴∠B=∠C，

∵AB=BD，

∴∠BAD=∠BDA，

∵CD=AD，

∴∠C=∠CAD，

∵∠BAD+∠CAD+∠B+∠C=180°，

∴5∠B=180°，

∴∠B=36°

故选：

B．

点评：

本题主要考查等腰三角形的性质，解题的关键是运用等腰三角形的性质得出∠BAD=2∠CAD=2∠B=2∠C关系．

4．（宜城市模拟）若等腰三角形一腰上的高和另一腰的夹角为25°，则该三角形的一个底角为（　　）

A．

32.5°

B．

57.5°

C．

32.5°或57.5°

D．

65°或57.5°

考点：

等腰三角形的性质．菁优网版权所有

分析：

题中没有指明这个等腰三角形的形状，故应该分情况进行分析，从而不难求解．

解答：

解：

①如图，∵∠ABD=25°，∠BDA=90°，

∴∠A=65°，

∵AB=AC，

∴∠C=（180°﹣65°）÷2=57.5°

②如图，

∵∠ABD=25°，∠BDA=90°，

∴∠BAD=65°，

∵AB=AC，

∴∠C=65°÷2=32.5°．

故选C．

点评：

此题主要考查等腰三角形的性质，三角形内角和定理及三角形外角的性质的综合运用，能够分类讨论是解答本题的关键．

5．（路南区一模）已知：

如图，l∥m，等边△ABC的顶点B在直线m上，边BC与直线m所夹锐角为20°，则∠α的度数为（　

　）

A．

60°

B．

45°

C．

40°

D．

30°

考点：

等边三角形的性质；平行公理及推论；平行线的性质．菁优网版权所有

专题：

计算题．

分析：

过C作CE∥直线m，由l∥m，推出l∥m∥CE，根据平行线的性质得到∠ACE=∠α，∠BCE=∠CBF=20°，即∠α+∠CBF=∠ACB=60°，即可求出答案．

解答：

解：

过C作CE∥直线m

∵l∥m，

∴l∥m∥CE，

∴∠ACE=∠α，∠BCE=∠CBF=20°，

∵等边△ABC，

∴∠ACB=60°，

∴∠α+∠CBF=∠ACB=60°，

∴∠α=40°．

故选C．

点评：

本题主要考查对平行线的性质，等边三角形的性质，平行公理及推论等知识点的理解和掌握，此题是一个比较典型的题目，题型较好．

二．填空题（共5小题）

6．（丽水）如图，在△ABC中，AB=AC，AD⊥BC于点D，若AB=6，CD=4，则△ABC的周长是　20　．

考点：

等腰三角形的性质．菁优网版权所有

专题：

几何图形问题．

分析：

运用等腰三角形的性质，可得BD=CD，再求出△ABC的周长．

解答：

解：

∵在△ABC中，AB=AC，

∴△ABC是等腰三角形，

又∵AD⊥BC于点D

∴BD=CD

∵AB=6，CD=4

∴△ABC的周长=6+4+4+6=20．

故答案为：

20．

点评：

本题主要考查等腰三角形的性质，一定要熟练掌握等腰三角形中的三线合一．

7．（澄海区模拟）已知实数x，y满足|x﹣4|+

=0，则以x，y的值为两边长的等腰三角形的周长是　10　．

考点：

等腰三角形的性质；非负数的性质：

绝对值；非负数的性质：

算术平方根；三角形三边关系．菁优网版权所有

分析：

先根据非负数的性质列式求出x、y的值，再分x的值是腰长与底边两种情况讨论求解．

解答：

解：

根据题意得，x﹣4=0，3y﹣6=0，

解得x=4，y=2，

①4是腰长时，三角形的三边分别为4、4、2，

能组成三角形，周长=4+4+2=10；

②4是底边时，三角形的三边分别为4、2、2，

不能组成三角形，

所以，三角形的周长为：

10；

故答案为：

10．

点评：

本题考查了等腰三角形的性质，绝对值与算术平方根的非负性，根据几个非负数的和等于0，则每一个算式都等于0求出x、y的值是解题的关键，难点在于要分情况讨论并且利用三角形的三边关系进行判断．

8．（晋江市质检）如图，在等腰△ABC中，AB=AC，AD⊥BC，若∠BAD=20°，则∠BAC=　40　度．

考点：

等腰三角形的性质．菁优网版权所有

分析：

等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合，依此即可求解．

解答：

解：

∵在△ABC中，AB=AC、AD⊥BC、

∴AD是△ABC的角平分线，

∵∠BAD=20°，

∴∠BAC=2∠BAD=40°．

故答案为：

40；

点评：

考查了等腰三角形三线合一的性质，题目难度不大，属于定理的直接应用．

9．（潜江模拟）已知等腰三角形有一个角是50°，则它的另外两个角是　65°或80°　．

考点：

等腰三角形的性质；三角形内角和定理．菁优网版权所有

专题：

计算题；分类讨论．

分析：

从当等腰三角形的顶角是50°时，当等腰三角形的底角是50°时两种情况进行分析，然后利用三角形内角和定理即可得出答案．

解答：

解：

当等腰三角形的顶角是50°时，其底角为：

=65°；

当等腰三角形的底角是50°时，其顶角为：

180﹣50×2=80°

故答案为：

65°或80°

点评：

此题主要考查学生对等腰三角形的性质和三角形内角和定理的理解和掌握，此类题目要用分类讨论的思想进行分析，不能遗漏．

10．（南安市一模）若等腰三角形两边长分别为10和5，则它的周长是　25　．

考点：

等腰三角形的性质；三角形三边关系．菁优网版权所有

分析：

根据腰为5或10，分类求解，注意根据三角形的三边关系进行判断．

解答：

解：

当等腰三角形的腰为5时，三边为5，5，10，5+5=10，三边关系不成立，

当等腰三角形的腰为10时，三边为5，10，10，三边关系成立，周长为5+10+10=25．

故答案为：

25．

点评：

本题考查了等腰三角形的性质，三角形三边关系定理．关键是根据已知边那个为腰，分类讨论．

三．解答题（共11小题）

11．（淄博）如图，AD∥BC，BD平分∠ABC．求证：

AB=AD．

考点：

等腰三角形的判定与性质；平行线的性质．菁优网版权所有

专题：

证明题．

分析：

根据AD∥BC，可求证∠ADB=∠DBC，利用BD平分∠ABC和等量代换可求证∠ABD=∠ADB，然后即可得出结论．

解答：

证明：

∵AD∥BC，

∴∠ADB=∠DBC，

∵BD平分∠ABC，

∴∠ABD=∠DBC，

∴∠ABD=∠ADB，

∴AB=AD．

点评：

此题主要考查学生对等腰三角形的判定与性质和平行线性质的理解和掌握，此题很简单，属于基础题．

12．（珠海）如图，在△ABC中，AB=AC，AD是高，AM是△ABC外角∠CAE的平分线．

（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）

（2）设DN与AM交于点F，判断△ADF的形状．（只写结果）

考点：

等腰三角形的判定与性质；作图—基本作图．菁优网版权所有

专题：

作图题；压轴题．

分析：

（1）以D为圆心，以任意长为半径画弧，交AD于G，交DC于H，分别以G、H为圆心，以大于

GH为半径画弧，两弧交于N，作射线DN，交AM于F．

（2）求出∠BAD=∠CAD，求出∠FAD=

×180°=90°，求出∠CDF=∠AFD=∠ADF，推出AD=AF，即可得出答案．

解答：

解：

（1）如图所示：

（2）△ADF的形状是等腰直角三角形，

理由是：

∵AB=AC，AD⊥BC，

∴∠BAD=∠CAD，

∵AF平分∠EAC，

∴∠EAF=∠FAC，

∵∠FAD=∠FAC+∠DAC=

∠EAC+

∠BAC=

×180°=90°，

即△ADF是直角三角形，

∵AB=AC，

∴∠B=∠ACB，

∵∠EAC=2∠EAF=∠B+∠ACB，

∴∠EAF=∠B，

∴AF∥BC，

∴∠AFD=∠FDC，

∵DF平分∠ADC，

∴∠ADF=∠FDC=∠AFD，

∴AD=AF，

即直角三角形ADF是等腰直角三角形．

点评：

本题考查了作图﹣基本作图，等腰三角形的性质和判定的应用，主要培养学生的动手操作能力和推理能力，题目比较典型，难度也适中．

13．（葫芦岛二模）已知如图，A（3，0），B（0，4），C为x轴上一点．

（1）画出等腰三角形ABC；

（2）求出C点的坐标．

考点：

等腰三角形的性质；坐标与图形性质．菁优网版权所有

专题：

计算题；作图题．

分析：

（1）根据A（3，0），B（0，4），C为x轴上一点．利用两点间的距离可分别求出C点坐标．

（2）设C（x，0），分3种情况①当A是顶点时，②当B是顶点时，③当C是顶点时三种情况进行讨论即可．

解答：

解：

设C（x，0），

（1）如图

（2）①当A是顶点时，C1（﹣2，0），C2（8，0），

②当B是顶点时，C3（﹣3，0）

③当C是顶点时，

．

点评：

此题主要考查等腰三角形的性质和坐标与图形性质等知识点，此题涉及到作图，难易程度适中，利用学生掌握基础知识．

14．（温州模拟）在下列四个条件中：

①AB=DC；②BE=CE；③∠B=∠C；④∠BAE=∠CDE．请选出两个作为条件，得出△AED是等腰三角形（写出一个即可），并加以证明．已知：

　①AB=DC；③∠B=∠C；或①AB=DC；④∠BAE=∠CDE．

或②BE=CE；③∠B=∠C；或②BE=CE；④∠BAE=∠CDE　；

求证：

△AED是等腰三角形．

考点：

等腰三角形的判定；全等三角形的判定与性质．菁优网版权所有

专题：

证明题．

分析：

根据“有两条边相等的三角形是等腰三角形”、“等角对等边”判定等腰三角形即可．

解答：

解：

可以选择填写：

①AB=DC；③∠B=∠C；或①AB=DC；④∠BAE=∠CDE．

或②BE=CE；③∠B=∠C；或②BE=CE；④∠BAE=∠CDE．

证明：

下面以①③为例证明

∵∠BEA=∠CDE、∠B=∠C、AB=DC

∴△AEB≌△DEC

∴AE=DE

∴△AED是等腰三角形．

点评：

本题考查了等腰三角形的判定与性质，熟记等腰三角形的判定定理是解决此题的关键与基础．

15．（昌平区一模）如图，已知△ABC和△ADE都是等边三角形，连接CD、BE．求证：

CD=BE．

考点：

等边三角形的性质；全等三角形的判定与性质．菁优网版权所有

专题：

证明题．

分析：

利用等边三角形的三边相等和各角都是60°，可证得△ADC≌△AEB，即可得结论．

解答：

证明：

∵△ABC和△ADE都是等边三角形，

∴AB=AC，AE=AD，∠DAE=∠CAB，

∵∠DAE﹣∠CAE=∠CAB﹣∠CAE，

∴∠DAC=∠EAB，

在△ADC和△AEB中，

∴△ADC≌△AEB．　　　

∴CD=BE．

点评：

本题考查了等边三角形的性质与全等三角形的判定与性质，正确的利用等边三角形中隐含的条件证明全等是解决本题的关键．

16．（白云区模拟）如图，△ABC中，BC∥AM，D是CA延长线上的一点，且∠B=∠DAM．

求证：

△ABC是等腰三角形．

考点：

等腰三角形的判定；平行线的性质．菁优网版权所有

专题：

证明题．

分析：

根据平行线的性质可得∠C=∠DAM，再利用等量代换求证∠B=∠C即可．

解答：

证明；

∵BC∥AM

∴∠C=∠DAM，

∵∠B=∠DAM

∴∠B=∠C，

∴AB=AC．

∴△ABC是等腰三角形．

点评：

此题主要考查等腰三角形的性质和平行线的性质等知识点的理解和掌握，难度不大，属于基础题．

17．（香洲区一模）△ABC是等腰三角形，AB=AC，∠A=36°．

（1）利用尺规作B的角平分线BD，交AC于点D；（保留作图痕迹，不写作法）

（2）判断△DBC是否为等腰三角形，并说明理由．

考点：

等腰三角形的判定与性质；三角形内角和定理；角平分线的性质；作图—基本作图．菁优网版权所有

专题：

作图题；证明题．

分析：

（1）以B为圆心，以任意长为半径画弧交AB、AC于两点，再以这两点为圆心，以大于这两点的距离的一半为半径画弧，交于一点，过这点和B作直线即可；

（2）由∠A=36°，求出∠C、∠ABC的度数，能求出∠ABD和∠CBD的度数，即可求出∠BDC，根据等角对等边即可推出答案．

解答：

（1）解：

如图所示：

（2）解：

△BCD是等腰三角形．

理由如下：

∵AB=AC，∠A=36°，

∴∠ABC=∠C=72°，

∵BD平分∠ABC，

∴∠DBC=

∠ABC=36°，

∴∠BDC=∠C=72°，

∴BC=BD，

∴△BCD是等腰三角形．

点评：

本题主要考查了等腰三角形的性质和判定，三角形的内角和定理，角平分线的性质，作图与基本作图等知识点，解此题的关键是能正确画图和求出∠C、∠BDC的度数．

18．（珠海）如图，在Rt△ABC中，∠ACB=90°．

（1）用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）

（2）连接AP，当∠B为　30　度时，AP平分∠CAB．

考点：

作图—基本作图；线段垂直平分线的性质．菁优网版权所有

专题：

作图题．

分析：

（1）运用基本作图方法，中垂线的作法作图，

（2）求出∠PAB=∠PAC=∠B，运用直角三角形解出∠B．

解答：

解：

（1）如图，

（2）如图，

∵PA=PB，

∴∠PAB=∠B，

如果AP是角平分线，则∠PAB=∠PAC，

∴∠PAB=∠PAC=∠B，

∵∠ACB=90°，

∴∠PAB=∠PAC=∠B=30°，

∴∠B=30°时，AP平分∠CAB．

故答案为：

30．

点评：

本题主要考查了基本作图，角平分线的知识，解题的关键是熟记作图的方法及等边对等角的知识．

19．（锦州）如图，在边长为1个单位长度的小正方形组成的网格中，按要求作图．

（1）利用尺规作图在AC边上找一点D，使点D到AB、BC的距离相等．（不写作法，保留作图痕迹）

（2）在网格中，△ABC的下方，直接画出△EBC，使△EBC与△ABC全等．

考点：

作图—复杂作图；全等三角形的判定；角平分线的性质．菁优网版权所有

专题：

作图题．

分析：

（1）作∠ABC的平分线即可；

（2）利用点A关于BC的对称点E画出△EBC．

解答：

解：

（1）如图，作∠ABC的平分线，

（2）如图，

点评：

本题主要考查了作图﹣复杂作图，角平分线的性质及全等三角形的判定，解题的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图．

20．如图，有ab两个村庄，a村距河边10米，b村距河边30米，两村的水平距离为30米，现要在河边建一抽水站，与铺设管道抽水到a村和b村（河的宽度小于10米）

（1）求铺设管道的最短距离是多少，请画图并求解；

（2）若铺设管道每米需要500元，则最低费用为多少？

考点：

作图—应用与设计作图．菁优网版权所有

分析：

（1）先求出点a关于河流的对称点a′，然后连接a′b，与河流的交点P即为所求作的抽水站的位置．利用勾股定理求出a′b即为铺设管道的最短距离．

（2）运用费用=米数×每米的钱数．

解答：

解：

（1）如图所示，抽水站修在点P处才能使所需的管道最短．

作bC垂直于河，a′C平行河．

∵两村的水平距离为30米，

∴a′C=30米．

∵a村距河边10米，b村距河边30米，

∴bC=10+30=40（米）．

∴a′b=

=

=50（米）．

（2）最低费用为：

50×500=25000（元）．

点评：

本题主要考查了作图﹣应用与设计作图，解题的关键是利用了轴对称的性质求解．

21．作图与证明按下列要求尺规作图（保留作图痕迹）：

如图，已知∠ABC，在边AB上有一点D，请过点D用尺规作出与BC平行的一条直线，并将你的理由填写在横线上．理由：

　同位角相等，两直线平行　．

考点：

作图—基本作图．菁优网版权所有

分析：

以点D为顶点，以DA为一边作角等于已知角，利用同位角相等两直线平行即可得到平行线．

解答：

解：

如图：

理由：

同位角相等，两直线平行．

点评：

本题考查了基本作图，解题的关键是了解如何作角等于已知角，难度不大．