工程力学C作业.docx

工程力学C作业.docx

《工程力学C作业.docx》由会员分享，可在线阅读，更多相关《工程力学C作业.docx（69页珍藏版）》请在冰豆网上搜索。

工程力学C作业

第1次作业

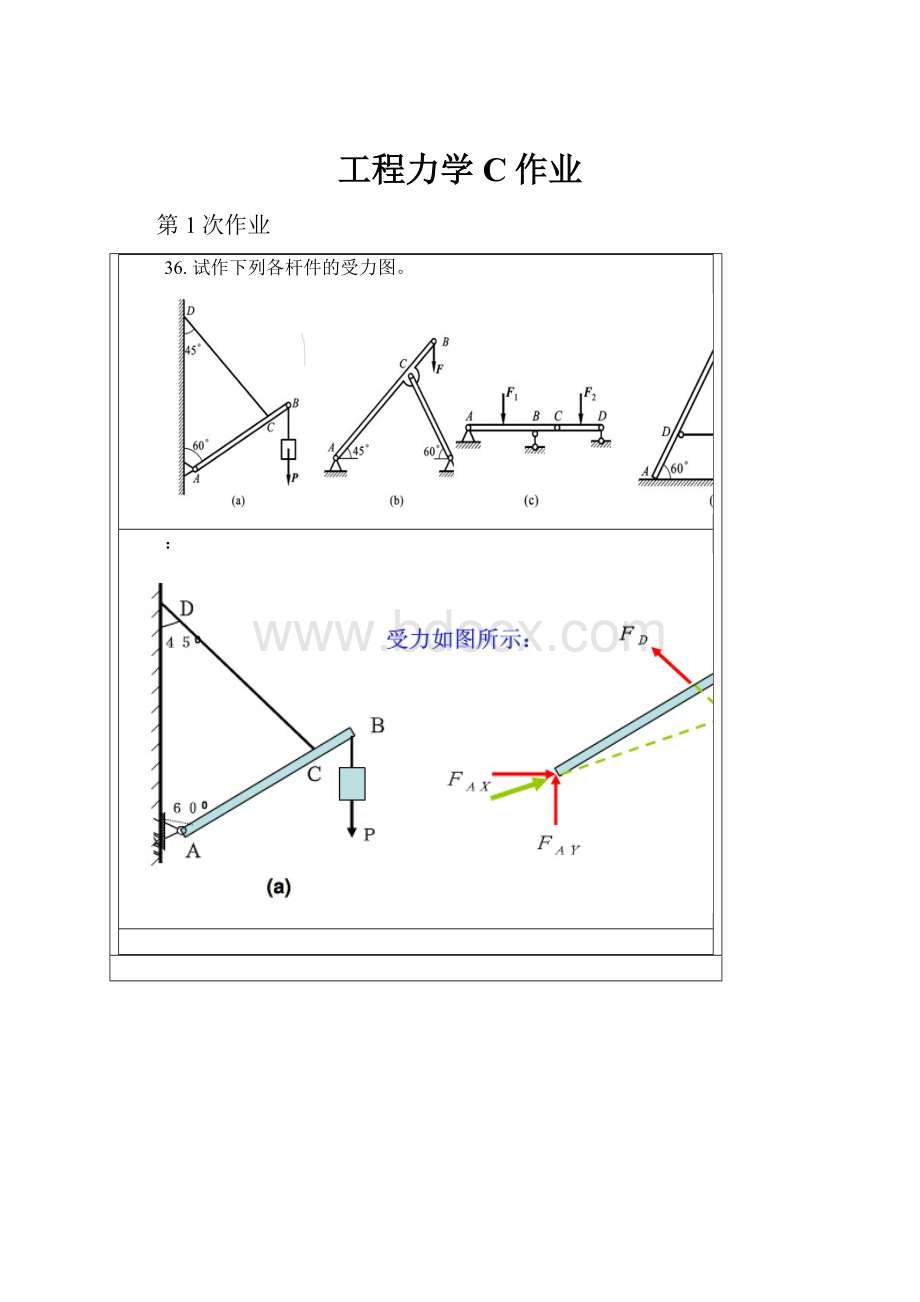
36. 试作下列各杆件的受力图。

：

37. 1-4试作下面物体系中各指定物体的受力图：

（a）圆柱体O、杆AB及整体；（b）吊钩G、钢梁、构件；

（c）折杆ABC、圆柱体O及整体；（d）杆AB及整体；

（e）棘轮O、棘爪AB；（f ）梁AB、DE和滚柱C。

38. 

图示三铰刚架由AB和BC两部分组成，A、C为固定铰支座，B为中间铰。

试求支座A、C和铰链B的约束力。

设刚架的自重及摩擦均可不计。

39. 

压路的碾子O重P = 20 kN，半径R = 400 mm。

试求碾子越过高度 = 80 mm的石块时，所需最小的水平拉力Fmin。

设石块不动。

：

Fmin=15kN

40. 构架ABCD在A点受力F = 1kN作用。

杆AB和CD在C点用铰链连接，B、D两点处均为固定铰支座。

如不计杆重及摩擦，试求杆CD所受的力和支座B的约束力。

41. 

梁AB如图所示，作用在跨度中点C的力F = 20 kN。

试求图示两种情况下支座A和B的约束力。

梁重及摩擦均可不计。

42. 

如图a所示，重量为P = 5 kN的球悬挂在绳上，且和光滑的墙壁接触，绳和墙的夹角为30º。

试求绳和墙对球的约束力。

（4）根据平衡条件列平衡方程。

可先求出各力在x、y轴上的投影，如表2-1中所示，于是

43. 

重P = 1 kN的球放在与水平成30º角的光滑斜面上，并用与斜面平行的绳AB系住（图2-15 a）。

试求绳AB受到的拉力及球对斜面的压力。

44. 

45. 

46. 

已知AB梁上作用一矩为Me的力偶，梁长为l，梁重及摩擦均不计。

试求在图示四种情况下支座A、B的约束力。

47. 

汽锤在锻打工件时，由于工件偏置使锤头受力偏心而发生偏斜，它将在导轨DA和BE上产生很大的压力，从而加速导轨的磨损并影响锻件的精度。

已知锻打力F = 1000 kN，偏心距e = 20 mm，锤头高度h = 200 mm

，试求锻锤给两侧导轨的压力。

48. 

机构OABO1，在图示位置平衡。

已知OA = 400 mm，O1B = 600 mm，作用在OA上的力偶的力偶矩之大小∣Me1∣= 1 N · m。

试求力偶矩Me2的大小和杆AB所受的力。

各杆的重量及各处摩擦均不计。

49. 

图中，如作用于扳手上的力F = 200 N，l = 0.40 m，α = 60º，试计算力对O点之矩。

50. 

试用合力矩定理计算图中力对O点之矩。

51. 

图 a所示梁AB受矩为Me = 300 N · m的力偶作用。

试求支座A、B的约束力。

第2次作业

20. 

压路的碾子O重P = 20 kN，半径R = 400 mm。

试求碾子越过高度δ = 80 mm的石块时，所需最小的水平拉力Fmin。

设石块不动。

：

Fmin=15kN

21. 

简易起重机用钢丝绳吊起重P = 2 kN的物体。

起重机由杆AB、AC及滑轮A、D组成，不计杆及滑轮的自重。

试求平衡时杆AB、AC所受的力（忽略滑轮尺寸）。

：

FAB=- 0.414kN（压），FAC=- 3.146kN（压）

22. 

在简支梁AB上，作用有力F = 50 kN，试求支座A和B的约束力。

不计梁重及摩擦力。

：

23. 

试求图中各力在坐标轴上的投影。

已知：

F1 = F2 = F4 = 10 kN，F3 = F5 = 15 kN，F6 = 20 kN，各力方向如图所示。

解：

应用教材中公式（2-3）得

F1x = F1 = 10 kN，F1y = 0，F2x = 0，F2y = F2 = 10 kN

F3x = F3 cos30º= 15 × 0.866 kN= 12.99 kN

F3y = F3 sin30º= 15 × 0.5kN = 7.50 kN

F4x = F4 sin30º= 10 × 0.5 kN= 5 kN

F4y = - F4 cos30º= - 10 × 0.866 kN= - 8.66 kN

F5x = F5 cos60º= 15 × 0.5kN = 7.50 kN

F5y = - F5 sin60º= - 15 × 0.866kN = - 12.99 kN

F6x = - F6 sin30º= - 20 × 0.5kN = - 10 kN

F6y = - F6 cos30º= - 20 × 0.866 kN= - 17.3 kN

24. 

在图示结构中，A、B、C处均为光滑铰接。

已知F = 400 N，杆重不计，尺寸如图所示。

试求C点处的约束力。

：

FCx=880N（→），FCy=480N（↓）

25. 

左端A固定而右端B自由的悬臂梁AB，自重不计，承受集度为q（N/m）的满布均匀荷载，并在自由端受集中荷载作用。

梁的长度为l。

试求固定端A

处的约束力。

：

FAx=0，FAy=ql+F（↑），MA= ql2+Fl

26. 

试分别求图中两根外伸梁其支座处的约束力。

梁重及摩擦均不计。

：

27. 

试分别求图示两个构架上A、B处所受到的约束力。

不计构件自重及各处的摩擦。

图b中C处为铰链。

：

28. 

图 a示一起重机，A、B、C处均为光滑铰链，水平梁AB的重量P = 4 kN，荷载F = 10 kN，有关尺寸如图所示，BC杆自重不计。

试求杆BC所受的拉力和铰链A给杆AB的约束力。

：

（1）根据题意，选AB为研究对象。

29. 

图 a所示梁AB，其A端为固定铰链支座，B端为活动铰链支座。

梁的跨度为l = 4a，梁的左半部分作用有集度为q的均布荷载，在D截面处有矩为Me的力偶作用。

梁的自重及各处摩擦均不计。

试求A和B处的支座约束力。

30. 

一汽车起重机，车身重P1，转盘重P2，起重机吊臂重P3，如图所示。

试求当吊臂在汽车纵向对称面内时，不至于使汽车翻倒的最大起重量Pmax。

31. 

试判别图示桁架中哪些杆其内力等于零，即所谓“零杆”。

你能否总结出判别零杆的规律？

（a）DE，EF，FG，BG（b）BC，AC

32. 

自重P = 1.0 kN的物块置于水平支承面上，受倾斜力F 1= 0.5 kN作用，并分别如图 a、b中所示。

物块与水平支承面之间的静摩擦因数f s= 0.40，动摩擦因数f d= 0.30，问在图中两种情况下物块是否滑动？

并求出摩擦力。

由于保持平衡所需的摩擦力F=0.433kN

值得注意的是，此时的摩擦力F=0.433kN是由平衡方程确定的，而不是Fmax=0.5kN。

只有在临界平衡状态，摩擦力才等于最大静摩擦力Fmax。

33. 

图示物块A置于斜面上，斜面倾角θ=30°,物块自重P=350N，在物块上加一水平力FT=100N,物块与斜面间的静摩擦因数fs=0.35,动摩擦因数fd=0.25。

试问物块是否平衡？

并求出摩擦力的大小和方向。

34. 

如图所示，长方体上作用了五个力，其中，F1=100N,F2=150N, F3=500N,F4=200N,F5=220N, 各力方向如图中所示。

且a=5m,b=4m,c=3m。

 试求各力在坐标轴上的投影.

35. 

36. 

：

F1x=130.0N，F1y=–75N，F1z=260.0N，F2x=100.0N，F2y=119.0N，F2z=156.0N

第3次作业

22. 

曲柄连杆机构的活塞上作用有力F = 400 N。

如不计摩擦和所有构件的重量，问在曲柄OA上应加多大的力偶矩Me方能使机构在图示位置平衡？

：

23. 

试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。

：

24. 

试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积

，试求各横截面上的应力。

：

25. 试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。

若横截面面积

，并求各横截面上的应力。

：

26. 简易起重设备的计算简图如图所示。

已知斜杆AB用两根

不等边角钢组成，钢的许用应力

。

试问在提起重量为

的重物时，斜杆AB是否满足强度条件？

：

27. 

图 a所示为左端固定而右端自由的轴向受力杆件。

试求Ⅰ-Ⅰ、Ⅱ-Ⅱ、Ⅲ-Ⅲ横截面上的轴力，并作轴力图。

：

28. 

一横截面为正方形的砖柱分上下两段，其受力情况、各段长度及横截面尺寸如图 a所示。

已知F = 50 kN，试求荷载引起的最大工作应力。

：

解：

首先作柱的轴力图如图 b所示。

由于此柱上下两段的横截面尺寸不同，故不能应用公式（7-3）计算柱的最大工作应力，必须利用公式（7-2）求出每段柱的横截面上的正应力，然后进行比较以确定全柱的最大工作应力。

Ⅰ、Ⅱ两段柱（图 a）横截面上的正应力分别为

29. 一横截面为矩形的钢制阶梯状直杆，其受力情况及各段长度如图a所示。

AD段和DB段的横截面面积为BC段横截面面积的两倍。

矩形截面的高度与宽度之比h/b=1.4，材料的许用应力、

=160MPa。

试选择各段杆的横截面尺寸h和b。

：

解：

首先作杆的轴力图如图 b所示。

此杆为变截面杆，最大工作应力不一定出现在轴力最大的AD段横截面上。

由于DB段的横截面面积与AD段相同，而轴力较小，故其工作应力一定小于AD段的。

于是只需分别对AD段和BC段进行计算。

对于AD段，按强度条件要求其横截面面积AI为

30. 

有一三角架如图所示，其斜杆由两根80×80×7等边角钢组成，横杆由两根10号槽钢组成，材料均为Q235钢，许用应力

= 120 MPa。

试求许用荷载[F]。

：

31. 

图 a所示为一阶梯形钢杆，AB段和BC段的横截面面积为A1 = A2 = 500 mm2，CD段的横截面面积为A3 = 200 mm2。

已知钢的弹性模量E = 2.0×105 MPa。

试求杆的纵向变形Δl。

图中长度单位为mm。

：

解：

此杆的轴力图如图b所示。

由于各段杆的轴力和横截面面积不尽相同，故须分段利用拉压胡克定律求各段杆的纵向变形，它们的代数和才是整个杆的纵向变形Δl。

32. 

试作图示各杆的轴力图，并分别指出最大拉力和最大压力的值及其所在的横截面（或这类横截面所在的区段）。

：

（a） AB段：

30 kN（拉），BC段：

0,CD段：

- 20kN（压）；

（b）  AB段：

10 kN（拉），BC段：

- 10kN（压），CD段：

20 kN（拉）；

（c） AB段：

0，  BC段：

10 kN（拉），CD段：

15 kN（拉）

33. 

试判定图示杆系是静定的，还是超静定的；若是超静定的，试确定其超静定次数，并写出求解杆系内力所需的位移相容条件（不必具体求出内力）。

图中的水平杆是刚性杆，各杆的自重均不计。

：

1次超静定

34. 

：

35. 

（1）最大切应力及两端截面间的相对扭转角；

（2）图示截面上A，B，C三点处切应力的数值及方向；

（3）C点处的切应变。

：

36. 

（1）最大切应力；

（2）截面A相对于截面C的扭转角。

37. 

：

38. 

：

39. 

一传动轴的计算简图如图 a所示，作用于其上的外力偶之矩的大小分别是：

MA = 2 kN · m，MB = 3.5kN · m，MC  = 1 kN · m，MD = 0.5kN · m，转向如图。

试作该传动轴的扭矩图。

：

40. 

一实心圆截面传动轴，其直径d = 40 mm，所传递的功率为30 kW，转速n = 1 400 r/min。

该轴由45号钢制成，许用切应力

= 40 MPa，切变模量G = 8×104 MPa，单位长度杆的许用扭转角

=1 /m。

试校核此轴的强度和刚度。

：

解：

首先计算扭转力偶矩M。

41. 

传动轴如图 a所示，其转速n=300r/min，主动轮A输入的功率P1 = 500 kW；若不计轴承摩擦所耗的功率，三个从动轮B、C、D输出的功率分别为P2 = 150 kW，P3 = 150 kW，P4 = 200 kW。

该轴是用45号钢制成的空心圆截面杆，其内外直径之比α = 1/2。

材料的许用切应力[τ ]= 40 MPa，其切变模量G=8×104MPa。

单位长度杆的许用扭转角

=0.3º/m。

试作轴的扭矩图，并按强度条件和刚度条件选择轴的直径。

42. 

试作图示各杆的扭矩图，并指出最大扭矩的值及其所在的横截面（或这些横截面所在的区段）。

：

（a） Tmax = Me；（b） Tmax = 2Me，在CD段；（c） Tmax = –3 kN·m，在DE段

43. 

直径50 mm的钢圆轴，其横截面上的扭矩T = 1.5 kN · m，试求横截面上的最大切应力。

：

44. 

空心钢圆轴的外直径D = 80 mm，内直径d = 62.5 mm，外力偶之矩Me = 10 N · m。

已知钢的切变模量G = 8×104 MPa。

①试作横截面上切应力的分布图；②试求最大切应力和单位长度扭转角。

：

45. 圆轴的直径d = 50 mm，转速为120 r/min。

若该轴横截面上的最大切应力等于60 MPa，试问所传递的功率是多少？

：

PkW = 18.5 kW

第4次作业

15. 

一根等直杆受力如图所示。

已知杆的横截面面积A和材料的弹性模量E。

试作轴力图，并求杆端点D的位移。

：

16. 

试求图示各梁中指定截面上的剪力和弯矩。

：

17. 

试指出图示剪力图和弯矩图的错误。

：

18. 

矩形截面的悬臂梁受集中力和集中力偶作用，如图所示。

试求截面m-m和固定端截面n-n上A，B，C，D四点处的正应力。

：

19. 

由两根28a号槽钢组成的简支梁受三个集中力作用，如图所示。

已知该梁材料为

Q235钢，其许用弯曲正应力

。

试求梁的许可荷载F。

：

20. 

：

21. 

：

22. 

试求图 a所示外伸梁指定横截面1-1、2-2、3-3、4-4上的剪力和弯矩。

：

23. 

图 a所示为一受满布均布荷载的悬臂梁。

试作此梁的剪力图和弯矩图。

：

解：

取x轴与梁的轴线重合，坐标原点取在梁的左端（图 a）。

以坐标x表示横截面的位置。

然后，求任意x处横截面上的剪力和弯矩，也就是找出横截面上剪力和弯矩与横截面位置的函数关系，我们分别把这种函数关系式叫做梁的剪力方程和弯矩方程。

为此，将梁在任意x处用横截面截开。

显然，就此梁而言，若取左段分离体为研究对象（图 b）则不必求支座约束力。

根据左段分离体的平衡条件便可列出剪力方程和弯矩方程如下：

以上两式后面括号里的不等式是用来说明对应的内力方程所适用的区段。

有了剪力方程和弯矩方程，便可在相应的坐标系里作出梁的剪力图（图 c）和弯矩图（图 d）。

此梁的剪力方程FS（x）= - qx表明FS（x）为x的线性函数，所以剪力图为一倾斜直线。

该直线可根据例如FS（0）= 0与FS（l）= - ql作出。

（注：

剪力方程在x = l处是不适用的，因该处有集中支座约束力。

此处取x为l，实际上是指l稍左一点的截面）。

作弯矩图时，表示弯矩M的纵坐标（图 d）取向下为正，以使梁的弯矩图始终位于梁的受拉一侧。

该梁的弯矩方程M（x）= - qx2 / 2表明M（x）是x的二次函数，弯矩图为二次抛物线。

在描点作图时至少需确定图线上的三个点，

例如，M（0）= 0，M（l / 2）= -  ql2，M（l）= -  ql2。

从内力图得知，固定端左侧横截面上的剪力和弯矩都有最大值，FS,max = ql，Mmax =  ql2（内力的最大值一般都以绝对值为准）。

24. 

对于图 a所示受满布均布荷载的简支梁，试作剪力图和弯矩图。

：

25. 

图 a所示为一受集中荷载作用的简支梁。

试作其剪力图和弯矩图。

：

26. 

试求图示诸梁中各指定的横截面上（1-1、2-2等）的剪力和弯矩。

：

（a） FS1 = FS2 =FS3 = 2 kN，M1 = - 3 kN·m，M2 = - 1 kN·m，M3 = - 4 kN·m

（b） FS1 = 0，FS2 =FS3 = - qa，FS4 = - qa，

   M1 = 0，M2 = M3 = - qa2，M4 = - qa2

（c） FS1 = ql，FS2 =FS3 = 0，M1 = M2 = M3 = ql2

（d） FS1 = FS2 =FS3 = ，M1 = ，M2 = ，M3 = - 

（e） FS1 = 3 kN，FS2 =FS3 = - 1.5 kN，M1 = M2 = - 0.6 kN·m，M3 = - 0.3 kN·m

（f） FS1 = FS2 = 0，FS3 = 1.17 qa，FS4 = 0.17 qa，M1 = M2 = M3 = qa2，M4 = 1.67 qa2

（g） FS1 = FS2 =FS3 = - 0.5 F，M1 = M2 = 0，M3 = - 0.25 Fl

（h） FS1 = - 0.5 ql，FS2 = - ql，FS3 = ql，M1 = - ql2，M2 = M3 =– ql2

27. 

试求图示折杆中各指定的横截面（1-1、2-2等）上的内力。

：

（a） FN1 = FN2 = 10 kN，FN3 = 0，FS1 = 0，FS2 = 0，FS3 = 10 kN

M1 = - 10 kN·m，M2 = - 10 kN·m，M3 = - 10 kN·m；

（b） FS1 = F，M1 = - Fa，T1 = 0；FS2 = F，M2 = 0，T2 = - Fa，

    FS3 = F，M3 = - Fl，T3 = -Fa

28. 

试写出图示各梁的剪力方程和弯矩方程，并作出剪力图和弯矩图。

指出最大剪力和最大弯矩的值以及它们各自所在的横截面。

：

（a） ∣FS,max∣ = 4 kN，∣Mmax∣ = 3 kN·m

（b） ∣FS,max∣ = 4 kN，∣Mmax∣ = 3 kN·m

（c） ∣FS,max∣ = qa，∣Mmax∣ = qa2

（d） ∣FS,max∣ = 56 kN，∣Mmax∣ = 192 kN·m

（e） ∣FS,max∣ = 9 kN，∣Mmax∣ = 12 kN·m

（f） ∣FS,max∣ = 15 kN，∣Mmax∣ = 30 kN·m

（g） ∣FS,max∣ = 1.5 F，∣Mmax∣ = Fa

29. 

在作剪力图和弯矩图时，作用于图a所示简支梁上的满布匀布荷载是否可以用图b所示的合力来代替？

这两种情况下的剪力和弯矩图各有什么不同？

：

不可以