 中考数学专题4几何模型之隐圆问题.docx
中考数学专题4几何模型之隐圆问题.docx
- 文档编号:25450219
- 上传时间:2023-06-08
- 格式:DOCX
- 页数:23
- 大小:268.65KB
中考数学专题4几何模型之隐圆问题.docx
《中考数学专题4几何模型之隐圆问题.docx》由会员分享,可在线阅读,更多相关《中考数学专题4几何模型之隐圆问题.docx(23页珍藏版)》请在冰豆网上搜索。
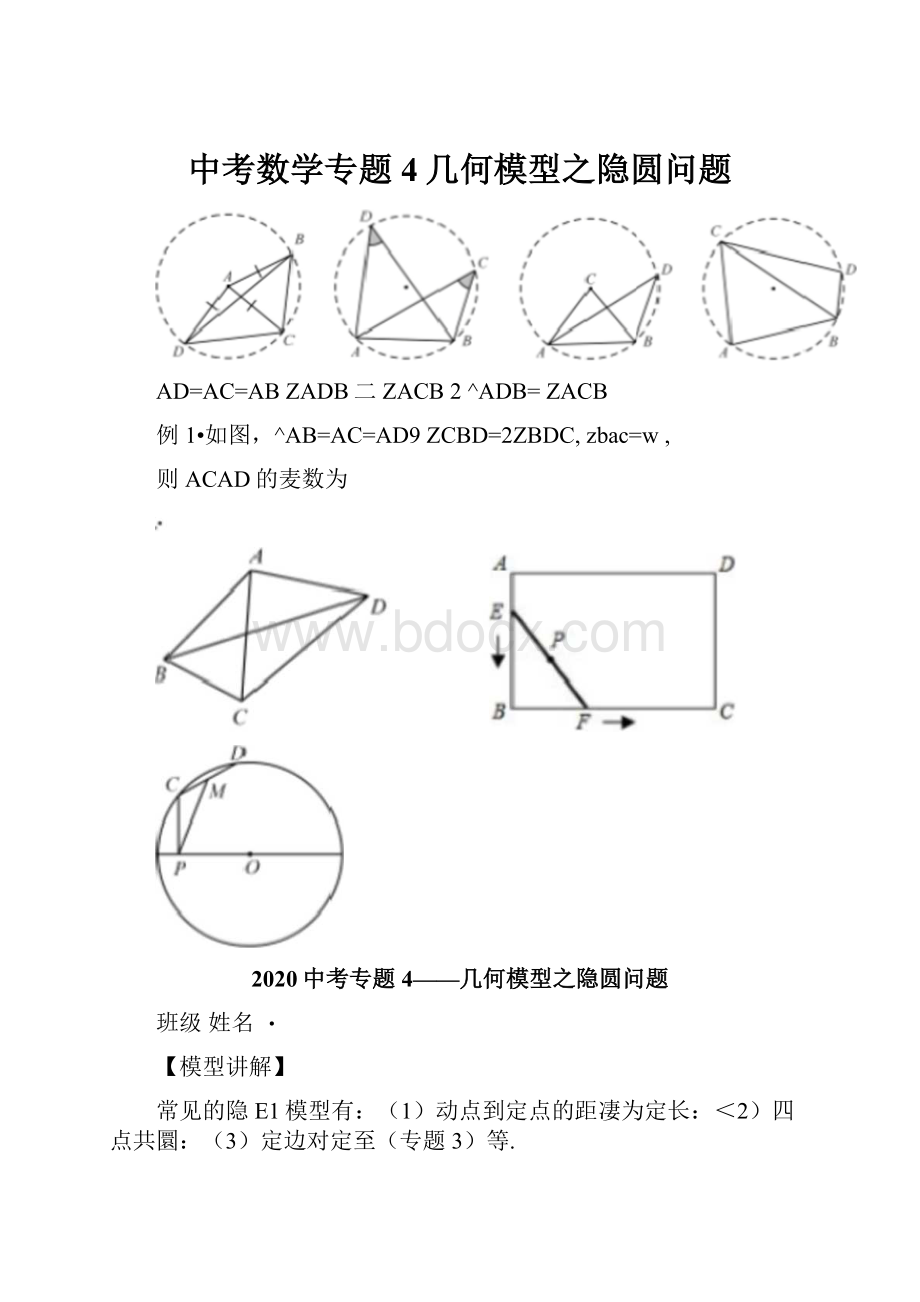
中考数学专题4几何模型之隐圆问题
AD=AC=ABZADB二ZACB2^ADB=ZACB
例1•如图,^AB=AC=AD9ZCBD=2ZBDC,zbac=w,
则ACAD的麦数为
2020中考专题4——几何模型之隐圆问题
班级姓名・
【模型讲解】
常见的隐E1模型有:
(1)动点到定点的距凄为定长:
<2)四点共圜:
(3)定边对定至(专题3)等.
ZBAC十ZBDC=130・
【例題分析】
例1底例299M3£
例2.在矩形ABCD中,己知肋■2沏,BC-3cm,现有一根长为2c加的木棒£F索贴着矩形的边(即两个端点姑终落在矩形的边上儿按逆时针方向滑动一間.则木燈刃的中点P在运动过程中所围成的SS形的面祝为cm2.
例3•如图,定饪弦CD在以肋为直径的OO上滑动(点C.D与点人3不重含〉•M是CD的中点,过点C作CP丄43于点”若AB=8,则PM的最大值是•
例4•如图,点/与点B的坐标分别是(1,0),C5,0)■点P是该直您坐标系内的一个动点・
(1〉使Z*PB=30・的点P有个$
(2〉若点P在y轴上,且ZAPB=3Q・,求漓足条件的点P的坐标;
(3)当点P在y轴上移动时."PB是否存在最大值?
若存在.求点P的坐标:
若不存在.请说明理由-
【巩固训练]
1•如图1,矩形"BCD中,4B.2,AD^3,点E.F分别Q、DC边上的点,且£F-2,点G为EF的中点•点P为BC上一动点.则P4+PG的最小值为•
图2
2•如图2,在矩形/BCD中,AB^4,AD^6f£是肋边的中点.F是找段BC边上的动点,将
A5SF沿£F所左直线折叠得到△EBT,连BD.则FD的最小值是—・
3•在平面直角坐标系中,点/的坐标为(3,0),点〃为〉•栢正半粧上的一点.点C是第一象P5内一点,KXC-2.设tanZBOC-wj则加的取«范團是・
4•如图3.往RtAABC中,ZC=90°,^C=6,BC=8,点F在边AC±9并且CF=2,点E为
边3C±的动点,将ACEF沿直线M和折,点C落在点P处,则点P到边距蘆的最小值
是
1
图4
5•如@04,四边形ABCD中,DC/iAB95C-1,AB^AC^AD^l.则加的长为.
6•如图5.在四边形ABCD中,・4B=/C=XZX若ZBAC=259,ZCAD=759•则ZBDC=_
ZDBC=•
7•定球射门.不考虑其他因素,仅考虑射点到球门肿的张介犬小时.张角越大,射门越好•如图6的正方形网格中,点A9B・C9D9E均在格点上,球员帝球沿CQ方向进攻,最好的射点在()
B.点D或点E
C•线段DE(异于毘点)上一点D•线段CD(异于端点)上一点
&如GE7.己知。
的査径,PQ是©0的弦,PQ与不平行.R是PQ的中点.作PSI
AB,QTLAB,垂足分别为S、T(SHE,芥且ZS2?
r=60・,则孕的值磚于_・
AB
9.如图&若PA=PB・ZAPB=2Z*CB,AC与PB交于点D,且PB=4・PD=3,则AD•DC=
10・左平页直角坐标系中.己知点H(4,OXB(一6,0〉■点C是y箱上的一个动点.当ZBCA=
43。
时,点C的坐标为.
11,如图9,RtaBC中,ZC=90°,XC=3,BC=4,点D在血边上,点E是BC边上一点(不
与点以C重合),且DA=DE,则3的取值范匡是・
12•如图10,在平面直角坐标系的第一象很内有一魚B,坐标为⑵w)•过点〃作AB±yfe9BC
丄x辭,垂足分别为儿C,若点P在线段肋上滑动(点P可以与点/、〃重合),发现使得Z0PC
=45-的位置有两个,则加的取直范圈为•
13.左锐坤△肋C中9AB=49BC=5fZACB=45Qf将△肋C绕点B按逆时针方甸贡转得到△A0C.(1〉如图11-1,当点C:
在线段C4的延长线上时,求ZCC凶的度数;
(2〉如图1卜2,连接心“CC\•若△如l的面积为4,求△(?
〃?
:
的面枳富
(3〉如图1卜3,点E为线段肋中点,点P是线段AC1.的动点,在3C绕点3技逆时针方向旋转过程中,点P的对应点是点P:
求线段£P:
长度的最犬值与最小值.
3
14•如刃,抛物线歹=一;分一:
工十3与x帕交于人B两点(点4在点B的左侧〉,与y轻交于点
C.
(1)求点A.B的坐标;
(2)若直线/过点E(4,0),M为直线/上的动点,当以*、B、M为顶点所作的直角三角形有且只有三个时,求直线/的解析式.
15.5QS,直线j=-|x+3与x轴、〉•轴分别交于B、4两点,点P是线段OB上的一动点,若能
在斜边肋上找到一点G使ZOCP=90・,设点P的坐标为g0),求加的取值范囲・
2020中考专题4
几何模型之隐圆问题参考答案
例1•【解^ab=ac=ad9
:
・B,C,Z)在以.4为21心,AB为半径的圆上,:
•乙CAD=2厶CBD.厶BAC=2/BDC、
•:
ZCBD=2ZBDC,ZBAC=449,•••ZCAD=2ZB&C=8丁.
故答案为:
88-•
例2【解答】解:
如图所示:
由题亘根克直角三角形斜边上的中线尊于斜边的一半,得出P到刃点距凄始终为1.
则木棒EF的中点P左运动过程中的轨迹为分别以乂,B,C,D为回心,15!
为半径的弧,故所围成的图形的面积为:
矩形面积-4个型形面积=6-4x驾;「=0一才(心).
故答案为:
6-穴・
例3・【解苔】解:
连按CO9A/O,
VZCPO=ZCW=90,,
AC,MO9P9四点共Eh且CO为直径(E为圆心九
连按PM则PM为0E的一条弦,当为直経时PM最大.所以PM=CO=4时PJ/最大.即PJ=4・
例4【解答】解:
(1)以肋为访,在第一象頃内作尊边三角形肋C,以点C为圆心,SC为半径作0G交y抽于点Pi.
在优弧APiB上任取一点P,如GE1,则ZAPB=丄Z-4CS=lx609=30*•
22
•••便Z加=30・的点P有无歎个.畝答案为,无数.
(2)①当点P在〉*的正半粕上时,过点C作QG丄A3,垂足为G如031.
•••点4(L0),点B(5,0),.*.04=1,OB=5.
:
.AB=4.
•••点C为国1心.CGIAB.:
.AG=BG=^AB=2.
2
:
.OG=OA^AG=3.
"ABC是等边三角形…・MC=BC=肋=4.
cg=VaC2-AG2=V42-22=2a^-
・••点C的坐标为<3,2苗).
过点C作CD一y轴,垂足为D.连按CP壮如391.
•••点C的坐标为(3,2V3)i:
・CD=3.OD=2>/3.
VPbP:
«0C与)轴的交点,:
・ZAPiB=ZAP:
B=30・.
•••CP尸CA=A,CD=39ADP2=J42.32=V7.
由smZ如违得:
当血
图2
•••点C为圆心,CQ丄PiPh:
.PiD=PiD=^/7.
:
・p、(o,2V3•西.Pi(0,2V3W7).
②当点P在y轴的负半轴上时,
同渥可得:
P3(0,・2^3•听〉•Pa(0,-2VW7).
综上所述:
满足条件的点P的坐标有:
(0,2^3•衙人(0,2、/5十听入(0,・2>/3・听〉.(0,•2岳听〉.
(3)当过点X.〃的0E与p紬相切于点P时,ZAPB最大.理由:
可证:
/APB=ZAEH,当Z加最大时,ZAEH最犬.
屡小即M最小时.厶最大•所以当图与[艳相切时,Z加最大・
①当点P在〉•轴的正半轴上时.
连按E4,作EH丄x轻,垂足为H.如图2・
V0£与j;轴相切于点P,:
・PE丄OP・
•:
EH丄肋.OP丄OH,:
•ZEPO=ZPOH=ZEHO=9y.•••囚边形OPEH是矩形.:
・OP=EH,PE=OH=3・:
.EA=3.VZEHA=909,AH=2・瓦4=3.
A£//=VeA2-AH2=V32-22=^5
AOP=V5:
・P(0,V5).
②当点p在〉•紿的负半轴上时,同淫可得:
P(0,-V5).
渥由,①若点P在〉•結的正半轴上.
左)轴的正半轴上任取一点"(不与点P重合〉,连按A纽沏,交OE于点N.连按NA,如區2所示.
VZANB是MMV的外角,•••^ANB>ZA\{B.
•厶APB=ZANB,:
•厶APB>厶ASiB・
②若点P在〉•轴的负半轴上,
间理可证得:
ZAPB>ZAXfB・
塚上所述:
当点P在J轴上移动时.厶APB有绘大值,此时点P的坐标为(0,V5)和(0,-V5).
【巩固训练】答案
1•解:
v£F-2■点G为EF的中点…・DG“,
•・・G是以D为圆心.以1为半径的21弧上的点,
作虫关于BC的对称点4,连按AD9交BC于P,交以D为E1心.
1为半径的圆于G,此时PAtPG的值最小,最小值为才G的长IAB■29AD-39AA9■4■ArD■59
:
.MG■才D-DG・5-】・4:
/.PA*PG的最小值为4:
故答案为4.
2•解:
如国所示点〃在以E为圆心以为半径的图上运动,当B\E关线时时.此时FD的值*小.
根据折直的性质,SEBF釜4EBE・•.Eff丄BfF,
:
・EB'=EB,
•••E是M边的中点,肋=4,
:
.AE=EB"=29
•••AD=6,
:
.DE=j6=,=2顶,
・・.BR=2顶-2.
3•解:
C在以4为E1心,以2为半径作K1周上,只有当0C与314相切(即到C点)时,ABOC绘小・
AC^290A^3f由勾股定理得:
0C-V5,
7ZBOA=XACO=90°,
••Z50C+厶OC-90SZC.4O+厶OC・90S
・・ABOC=AOAC,
tanZBOC=tanZ.OAC
ocVs
=I
AC2
随着C的移动,"OC越来越大,
•••c在第一象限,:
・C不到汇轴爲即级C—.ta^OC耳,故答案为,
75
2•
4•解,如图所示,当PE//AB.
左RtlABC中,vZC-90°,FC・6,BC・8・
由期折的性质可知:
PF・FC・2,Z.FPE-ZC-906.•:
PEHAB■
/.ZPDB-90°.
由垂线段最短可知此时"有最小值.又•••朋为定值,
:
PD有最小值.
又•••厶ZACB^^ADF9:
.MFD5MBC.
•••PD・DF-FP・32・2・L2・
5•解,以川为圆心,/1B长为半包作HI,延长BA交64于F,连按DF.
•••FB是0/的直径,・・・"DB=9Q°■二BD=dBF、-DF'=屈・
6.【解答】解:
法一:
9:
AB=AC=AD9
:
.zadb=^abd9zacb=zabc9zadc=zacd,
•••ZA4C=25・,ZCAD=159,
:
・ZACB=C180*-25*)「2=77.5*,ZDAB=ZDAC+ZCAB=\g,
ZADC=ZACD=(180s•75°)4-2=52.5*,
AZADB=C180*・100,)十2=40*,
:
・ZBDC=ZADC・/ADB=525。
・40°=12.5’,
ZDCB=ZDCA+ZACB=525・+77.5*=130",
AZZ>3C=1803・ZDCB・ZBDC=\8L-130s-12.5°=37.59••••"DC=\25・,ZDBC=3"・.
7.【解答】解:
连^BCfACfBD,AD,AEfBEf
己知儿B.DE四点共圆,同弧所对的圆亶角相等,m^ZADB=ZAEB9然后KI同孤对应的“31内危“大于13周理「圆外角“小于01周角,因而射门点在皿上时介最九射门点在D点右上方或点E左下方时角度则会更小.
故选,C.
8•【解签】锌,连结OP,OQ9OR,如05,
TA是P0的中点■:
・OR丄P0
•:
OP=OQ,•••ZPOR=ZQQR,
TPS丄肋.・・・ZPSO=ZPRO=9Q・,
•••点P、S.6R四点在以OP为直径的a±,:
・ZPSR=ZPOR,
同理可得ZQTR=ZQOR,:
•乙PSR=ZQTR.:
.ZRST=ZRTS9而ZSRT=609,
:
.HRST为等边三角形.•••ZRST=60・•ZRTS=6099
:
・ZRPO=ZRSO=6W,ZRQO=ZRTO=6W,:
・M)PQ为等边三箱形,
:
・PQ=OP.:
.AB=2PQ9•••匹=丄・故答案为丄.
AB22
9•解析:
本超主更考査三点共01判定和相交弦定理.
由刃=PB,"PB=2乙ACB,可知,A,B,C三点芜固,E)心为P半径为PB・由梅交弦定理可知*AD・DC=(PB・PD)(PB-PD)=7
10•【解答】解,设线段B4的中点为E
T点戏(4.0人B—6.0),:
.AB=1Q.E(・1.0).
(1)如答图1所示,过点E在第二象刀作EP丄04且刃=丄43=5,则易知“PBd为垂素直
2
角三角形・Z朋4=90°,PA=PB=5>/2;
以点P为引心,PA(或P5)长为半径作G)P,与y牠的正半璀文于点C,
VZBCA为。
P的E1局走,•••ZBC4=丄Z8刃=45・,即则点C即为所求・
2
过点P作PF丄丁雜于点F,^OF=PE=5,PF=1,
在RtAPFC中,PF=1,PC=&\/2,由勾股定瑾得:
CF=7pc2TpP=7»
:
.OC=OF+CF=5+7=12,
•••点C坐标为(0,12):
C2)如答B32所示,在第3至踐可以參觅
(1)作同样探作,同理求得)扮负半轴上的虑O坐标为(0,・12).
综上所述,点C坐标为(0,12)或(0,・12).
故答案为*(0.12〉或(6・12〉.
11•【解答】7RIA4BC中,NC=90・,AC=3,BC=4,
A^=^ac2+bc2=5,以Z)为El心,AD的长为半径甄0D
①如图1,当OD与万Ctfl切时,DE丄BC时,
设AD=x9则DE=AD=x9BD=AB・AD=5•心
•:
ZBED=ZC=9Q・,ZB是公共角,
•••△BDEs△朋°•••型史匕^—~9解險x=-^i
ABAC538
・・・Q的取值范圈是守W
②如图2.当OD与0C相交时.若文点为B或C,贝UD=
12.【解答】輕:
如医3中,在x箱上方作△0KC,使得ZiOKC是以OC为斜边的等養直角三角形,作AZ丄
于£・
VOC=2,
:
・OK=KC=近,
当EK=KC=y/2^f以K为圜心,KC为半径的卿与加堆切,此时加
=3C=1#近,在曲上只有一个点P满足ZOPC=丄Z0KC=4亍,
2
当BK=近时,在曲上恰好有两个点P满足ZOPC=丄ZOKC=455,
2
此时m=BC=29
综上所述,满足条件的加的值的范匿为2Wmd・
故答案为2W/V1+近・
13.【整答】怜
(1)由炭转的性质可律:
ZAiCiB=ZACB=459,BC=BC“
•.ZCCi5=ZCiC5=459,
•.ZCCiAi=ZCCiB^ZA\CiB=459+45,=90f・
(2)•••厶磁空△如BC】,
•・BA=BA\,BC=BC“/ABC=ZA\BC“
BABA】
ZABC+乙ABCi=/KBCbZABCx
BCBC]
ZABAi=ZCBC\f:
.LABAx^^CBCi.
SAADA
SACBCl
g)
:
s丄A41=4.••S^CBCX=—-:
4
(3)①如图1,过点〃作3D丄XC,D为垂足,:
WBC为锐矩三角形…••点D在线段AC±9在RtASCD申.5D=5CXsin45t=
-2:
当卩在AC1.运动.3P与/C垂直的时候.AABC绕点B媒捷,使点P的对圧点P】在线段肋上时.EPi聂小,最小值为:
EPi=BP「BE=BD・BE=
②当P在XC上运动至点C,HABC绕点B贯转,便点P的灯应点Pi在线段AB的延上銭上时.EPl最大,最大值为*EP产BC・BE=2+5=1.
KI
14.[解答】韬
(1)令y=0,即上孑上3=0,
84
解得口=・4,x2=2,
•"、3点的坐标为/!
<-4,OXB(2,0).
(2)抛物线y=丄/』x+3的对称粧是直线k=・——=・1,
842X(峙)
即D点的横坐标杲•1,
S土cb="^45・QC=9,
2
在Rtd4OC中,^C=^0A2f0C2=^42+32=5,设"C刀中AC^l上的高为儿则有—C讪=9,解得*=垒・
25
如答罔1,在坐标平面内作直线平行于2C,且到AC的距蔑=力=¥,这样的直线有2条,分别是h和h,则直线与对称轴x=・1的两个交点即为所求的点D・
设h交》紬于E,过C作CF丄h于尸,贝iJCF=/i=丄3,
28
・CE=—^-X=9
••s_sinZCEF*sinZXA"£一兀
r
设直线/ Y20,解得.b=3 rk^ 得到* k_4, 23 •••直线AC解析式为y=丄"3. 4 直线h可以看做直线AC^下平移CE也度单位个长度单位)而形成的. 2 •••直经A的解祈式为>=丄"3-2=壬・1. 4242 则Di的纵坐标为2x(.1)・色=2-2.). 4244 间孔直^AC向上平移刍个长厦址位得到匕可求得D(・1.空〉 24 综上所述•D点坐标为*Dj(-1>J-),D2(・1.互〉. 44 (3〉如答图2,以/方为直径作O氏05心为E过£点作0F的切线,这样的切线有2条.连接FM过M作kN丄x轴于点N. 0),B(2,0), : .F(-1,0),0F半径FM=FB=3・又TE(4,0), : ・FE=5, 在RtAMEF中,述=餉刁孑=4,sinZ.WF^=l,cosNMFE=』・55 在Rt△用MV中,A£V=N£F・sinZME=3x2=I^ 55 ^=^-cosZ.WF5=3xA=2,则av=l, 555 •••M点坐标为(±歿) 55 直线/过M(土丄Z).E(4,0), 55 设直线/的解折式为y=kx±b,则有 一4, b=3 所以直线/的解析式为y=令+3 '詼Z乎,和卜2 4k+b=0 同岂可以求得另一条切线的解析式为・3・4 综上所述,直线/的解析式为少=鸟+3或>・=丄—3・ 44 15.方法提示】令y=O求出点B的坐标■过点C作CD丄x箱于D.设点C的横坐标为a. 则ODn,PD=m-a,求出AOCD和MPD相似,刘用相似三角形对应边成比例列式表示岀m.然右求出m的最小值: 再根据点P在线段OB上判断出OC丄AB时.点P、B盍合,m圮大•然方即可写tBm的取值范團・ m的取值范围是3SmS4・
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 中考 数学 专题 几何 模型 问题
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 《爱和自由》读书心得15篇.docx
《爱和自由》读书心得15篇.docx
 人才工作计划完成情况表(精荐).xls
人才工作计划完成情况表(精荐).xls
