初中几何中线段和差的最大值与最小值典型分析最全.docx

初中几何中线段和差的最大值与最小值典型分析最全.docx

《初中几何中线段和差的最大值与最小值典型分析最全.docx》由会员分享，可在线阅读，更多相关《初中几何中线段和差的最大值与最小值典型分析最全.docx（21页珍藏版）》请在冰豆网上搜索。

初中几何中线段和差的最大值与最小值典型分析最全

初中几何中线段和（差）的最值问题

一、两条线段和的最小值。

基本图形解析：

（对称轴为：

动点所在的直线上）

一）、已知两个定点：

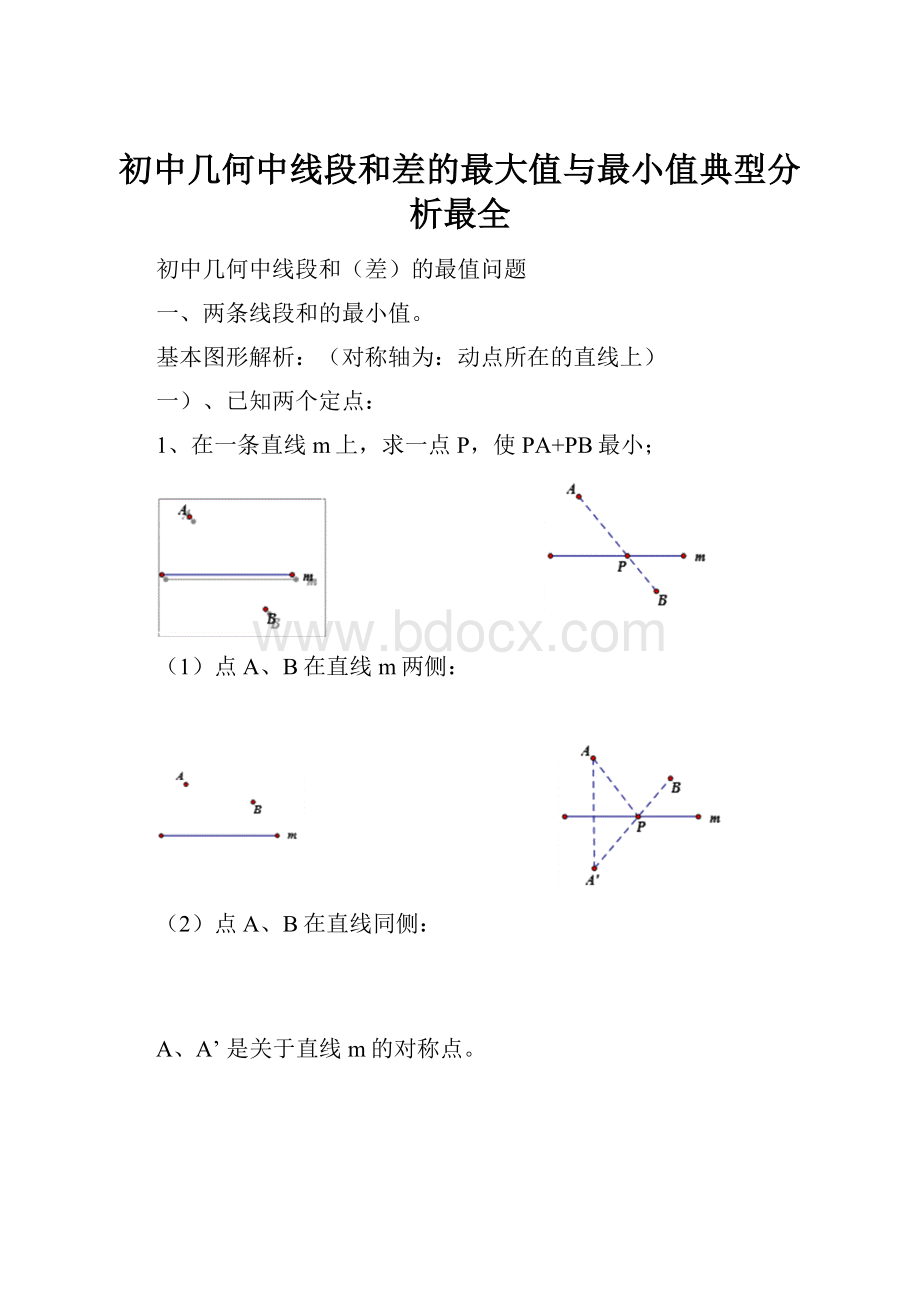
1、在一条直线m上，求一点P，使PA+PB最小；

（1）点A、B在直线m两侧：

（2）点A、B在直线同侧：

A、A’是关于直线m的对称点。

2、在直线m、n上分别找两点P、Q，使PA+PQ+QB最小。

（1）两个点都在直线外侧：

（2）一个点在内侧，一个点在外侧：

（3）两个点都在内侧：

（4）、台球两次碰壁模型

变式一：

已知点A、B位于直线m,n的内侧，在直线n、m分别上求点D、E点，使得围成的四边形ADEB周长最短.

填空：

最短周长=________________

变式二：

已知点A位于直线m,n的内侧,在直线m、n分别上求点P、Q点PA+PQ+QA周长最短.

二）、一个动点，一个定点：

（一）动点在直线上运动：

点B在直线n上运动，在直线m上找一点P，使PA+PB最小（在图中画出点P和点B）

1、两点在直线两侧：

2、两点在直线同侧：

（二）动点在圆上运动

点B在⊙O上运动，在直线m上找一点P，使PA+PB最小（在图中画出点P和点B）

1、点与圆在直线两侧：

2、点与圆在直线同侧：

三）、已知A、B是两个定点，P、Q是直线m上的两个动点，P在Q的左侧,且PQ间长度恒定,在直线m上要求P、Q两点，使得PA+PQ+QB的值最小。

（原理用平移知识解）

（1）点A、B在直线m两侧：

过A点作AC∥m,且AC长等于PQ长，连接BC,交直线m于Q,Q向左平移PQ长，即为P点，此时P、Q即为所求的点。

（2）点A、B在直线m同侧：

练习题

 1．如图，∠AOB=45°，P是∠AOB内一点，PO=10，Q、R分别是OA、OB上的动点，求△PQR周长的最小值为             ．

2、　如图1，在锐角三角形ABC中，AB=4

∠BAC=45°，∠BAC的平分线交BC于点D，M,N分别是AD和AB上的动点，则BM+MN的最小值为             ．

3、如图，在锐角三角形ABC中，AB=

，∠BAC=45，BAC的平分线交BC于D，M、N分别是AD和AB上的动点，则BM+MN的最小值是多少？

4、如图4所示，等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边上一点.若AE=2,EM+CM的最小值为         .

5、如图3，在直角梯形ABCD中，∠ABC＝90°，AD∥BC，AD＝4，AB＝5，BC＝6，点P是AB上一个动点，当PC＋PD的和最小时，PB的长为__________．

6、　如图4，等腰梯形ABCD中，AB=AD=CD=1，∠ABC=60°，P是上底，下底中点EF直线上的一点，则PA+PB的最小值为              ．

7、如图5菱形ABCD中，AB=2，∠BAD=60°，E是AB的中点，P是对角线AC上的一个动点，则PE+PB的最小值为            ．

8、如图，菱形ABCD的两条对角线分别长6和8，点P是对角线AC上的一个动点，点M、N分别是边AB、BC的中点，则PM+PN的最小值是            

9、如图，圆柱形玻璃杯，高为12cm，底面周长为18cm，在杯内离杯底3cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为________cm．

10、如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为            

 11、如图，正方形ABCD的边长为2，E为AB的中点，P是AC上一动点．则PB+PE的最小值是

12、　如图6所示，已知正方形ABCD的边长为8，点M在DC上，且DM=2，N是AC上的一个动点，则DN+MN的最小值为           ．

13、如图，正方形ABCD的边长是2，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值为          ．

14、如图7，在边长为2cm的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为                    cm．（结果不取近似值）．

15、如图，⊙O的半径为2，点A、B、C在⊙O上，OA⊥OB，∠AOC=60°，P是OB上一动点，则PA+PC的最小值是．

16、如图8，MN是半径为1的⊙O的直径，点A在⊙O上，∠AMN＝30°，B为AN弧的中点，P是直径MN上一动点，则PA＋PB的最小值为（   ）

（A）2

   （B） 

    （C）1   （D）2

解答题

1、如图9，正比例函数y=

x的图象与反比例函数y=

（k≠0）在第一象限的图象交于A点，过A点作x轴的垂线，垂足为M，已知三角形OAM的面积为1.

（1）求反比例函数的解析式；

（2）如果B为反比例函数在第一象限图象上的点（点B与点A不重合），且B点的横坐标为1，在x轴上求一点P，使PA+PB最小.

2、如图，一元二次方程x2+2x-3=0的二根x1，x2（x1＜x2）是抛物线y=ax2+bx+c与x轴的两个交点B，C的横坐标，且此抛物线过点A（3，6）．

（1）求此二次函数的解析式；

（2）设此抛物线的顶点为P，对称轴与AC相交于点Q，求点P和点Q的坐标；

（3）在x轴上有一动点M，当MQ+MA取得最小值时，求M点的坐标． 

3、如图10，在平面直角坐标系中，点A的坐标为（1，

），△AOB的面积是

.

（1）求点B的坐标；

（2）求过点A、O、B的抛物线的解析式；

（3）在

（2）中抛物线的对称轴上是否存在点C，使△AOC的周长最小？

若存在，求出点C的坐标；若不存在，请说明理由；

4．如图，抛物线y＝

x2－

x＋3和y轴的交点为A，M为OA的中点，若有一动点P，自M点处出发，沿直线运动到x轴上的某点（设为点E），再沿直线运动到该抛物线对称轴上的某点（设为点F），最后又沿直线运动到点A，求使点P运动的总路程最短的点E，点F的坐标，并求出这个最短路程的长．

5．如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴于点E和F．

（1）求经过A、B、C三点的抛物线的解析式；

（2）当BE经过

（1）中抛物线的顶点时，求CF的长；

（3）在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ＝1，要使四边形BCPQ的周长最小，求出P、Q两点的坐标．

 6．如图，已知平面直角坐标系，A，B两点的坐标分别为A（2，－3），B（4，－1）若C（a，0），D（a+3，0）是x轴上的两个动点，则当a为何值时，四边形ABDC的周长最短．

7、如图11，在平面直角坐标系中，矩形

的顶点O在坐标原点，顶点A、B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.

（1）若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；

（2）若E、F为边OA上的两个动点，且EF=2，当四边形CDEF的周长最小时，求点E、F的坐标.

二、求两线段差的最大值问题（运用三角形两边之差小于第三边）

基本图形解析：

1、在一条直线m上，求一点P，使PA与PB的差最大；

（1）点A、B在直线m同侧：

解析：

延长AB交直线m于点P，根据三角形两边之差小于第三边，P’A—P’B＜AB，而PA—PB=AB此时最大，因此点P为所求的点。

（2）点A、B在直线m异侧：

解析：

过B作关于直线m的对称点B’,连接AB’交点直线m于P,此时PB=PB’，PA-PB最大值为AB’

练习题

1.如图，抛物线y＝－

x2－x＋2的顶点为A，与y轴交于点B．

（1）求点A、点B的坐标；

（2）若点P是x轴上任意一点，求证：

PA－PB≤AB；

（3）当PA－PB最大时，求点P的坐标.

2.如图，已知直线y＝

x＋1与y轴交于点A，与x轴交于点D，

抛物线y＝

x2＋bx＋c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．

（1）求该抛物线的解析式；

（3）在抛物线的对称轴上找一点M，使|AM－MC|的值最大，求出点M的坐标．

3、在直角坐标系中，点A、B的坐标分别为（－4，－1）和（－2，－5）；点P是y轴上的一个动点，⑴点P在何处时，PA＋PB的和为最小？

并求最小值。

⑵点P在何处时，∣PA—PB∣最大？

并求最大值。

4.如图，直线y＝－

x＋2与x轴交于点C，与y轴交于点B，点A为y轴正半轴上的一点，⊙A经过点B和点O，直线BC交⊙A于点D．

（1）求点D的坐标；

（2）过O，C，D三点作抛物线，在抛物线的对称轴上是否存在一点P，使线段PO与PD之差的值最大？

若存在，请求出这个最大值和点P的坐标．若不存在，请说明理由．

5、抛物线的解析式为

，交x轴与A与B,交y轴于C，

⑴在其对称轴上是否存在一点P，使⊿APC周长最小，若存在，求其坐标。

⑵在其对称轴上是否存在一点Q，使∣QB—QC∣的值最大，若存在求其坐标。

6、已知：

如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连接MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO．

（1）试直接写出点D的坐标；

（2）已知点B与点D在经过原点的抛物线上，点P在第一象限内的该抛物线上移动，过点P作PQ⊥x轴于点Q，连接OP．

①若以O、P、Q为顶点的三角形与△DAO相似，试求出点P的坐标；

②试问在抛物线的对称轴上是否存在一点T，使得|TO-TB|的值最大？

7、如图，已知抛物线C1的解析式为y=-x2+2x+8，图象与y轴交于D点，并且顶点A在双曲线上．

（1）求过顶点A的双曲线解析式；

（2）若开口向上的抛物线C2与C1的形状、大小完全相同，并且C2的顶点P始终在C1上，证明：

抛物线C2一定经过A点；

（3）设

（2）中的抛物线C2的对称轴PF与x轴交于F点，且与双曲线交于E点，当D、O、E、F四点组成的四边形的面积为16.5时，先求出P点坐标，并在直线y=x上求一点M，使|MD-MP|的值最大．

8、如图,已知抛物线经过A（3，0），B（0，4），

（1）.求此抛物线解析式

（2）若抛物线与x轴的另一交点为C，求点C关于直线AB的对称点C’的坐标

（3）若点D是第二象限内点，以D为圆心的圆分别与x轴、y轴、直线AB相切于点E、F、H，问在抛物线的对称轴上是否存在一点一点P，使得|PH－PA|的值最大？

若存在，求出该最大值；若不存在，请说明理由。

三、其它非基本图形类线段和差最值问题

1、求线段的最大值与最小值需要将该条线段转化到一个三角形中，在该三角形中，其他两边是已知的，则所求线段的最大值为其他两线段之和，最小值为其他两线段之差。

2、在转化较难进行时需要借助于三角形的中位线及直角三角形斜边上的中线。

3、线段之和的问题往往是将各条线段串联起来，再连接首尾端点，根据两点之间线段最短以及点到线的距离垂线段最短的基本依据解决。

1、如图，在△ABC中，∠C=90°，AC=4，BC=2，点A、C分别在x轴、y轴上，当点A在x轴上运动时，点C随之在y轴上运动，在运动过程中，点B到原点的最大距离是（）

A．

B．

C。

D．6

2、已知:

在△ABC中，BC=a，AC=b，以AB为边作等边三角形ABD.探究下列问题:

（1）如图1，当点D与点C位于直线AB的两侧时，a=b=3，且∠ACB=60°，则CD=；

（2）如图2，当点D与点C位于直线AB的同侧时，a=b=6，且∠ACB=90°，则CD=；

（3）如图3，当∠ACB变化,且点D与点C位于直线AB的两侧时，求CD的最大值及相应的∠ACB的度数.

图1图2图3

3、在Rt△ABC中，∠ACB=90°，tan∠BAC=

.点D在边AC上（不与A，C重合），连结BD，F为BD中点.

（1）若过点D作DE⊥AB于E，连结CF、EF、CE，如图1．设

，则k=；

（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：

BE-DE=2CF；

（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．

4、如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM.⑴求证：

△AMB≌△ENB；

⑵①当M点在何处时，AM＋CM的值最小；

②当M点在何处时，AM＋BM＋CM的值最小，并说明理由；

⑶当AM＋BM＋CM的最小值为

时，求正方形的边长.

2、你知道日食的形成过程吗？

答：

放大镜的中间厚，边缘薄，光线在透过放大镜时会产生折射，因此会把物图像放大。

5、如图，二次函数y=-x2+bx+c与x轴交于点B和点A（-1，0），与y轴交于点C，与一次函数y=x+a交于点A和点D．

（1）求出a、b、c的值；

（2）若直线AD上方的抛物线存在点E，可使得△EAD面积最大，求点E的坐标；

（3）点F为线段AD上的一个动点，点F到

（2）中的点E的距离与到y轴的距离之和记为d，求d的最小值及此时点F的坐标．

12、放大镜和显微镜的发明，大大扩展了我们的视野，让我们走进微小世界，让我们看到了微生物和细胞。

1、焚烧处理垃圾的优缺点是什么？

答：

火柴燃烧、铁钉生锈、白糖加热等。

7、硫酸铜溶液与铁钉的反应属于化学反应。

硫酸铜溶液的颜色是蓝色，将铁钉浸入硫酸铜溶液中，我们发现铁钉变红了。

14、在太阳周围的八颗大行星，它们是水星、金星、地球、火星、木星、土星、天王星、海王星。

3、我们在水中发现了什么微生物呢？

（P18）

7、硫酸铜溶液与铁钉的反应属于化学反应。

硫酸铜溶液的颜色是蓝色，将铁钉浸入硫酸铜溶液中，我们发现铁钉变红了。

14、在显微镜下观察物体有一定的要求。

物体必须制成玻片标本，才能在显微镜下观察它的精细结构。