微积分学习方法一天学会微积分.docx

微积分学习方法一天学会微积分.docx

《微积分学习方法一天学会微积分.docx》由会员分享，可在线阅读，更多相关《微积分学习方法一天学会微积分.docx（23页珍藏版）》请在冰豆网上搜索。

微积分学习方法一天学会微积分

先看数

Yee22:

20:

30

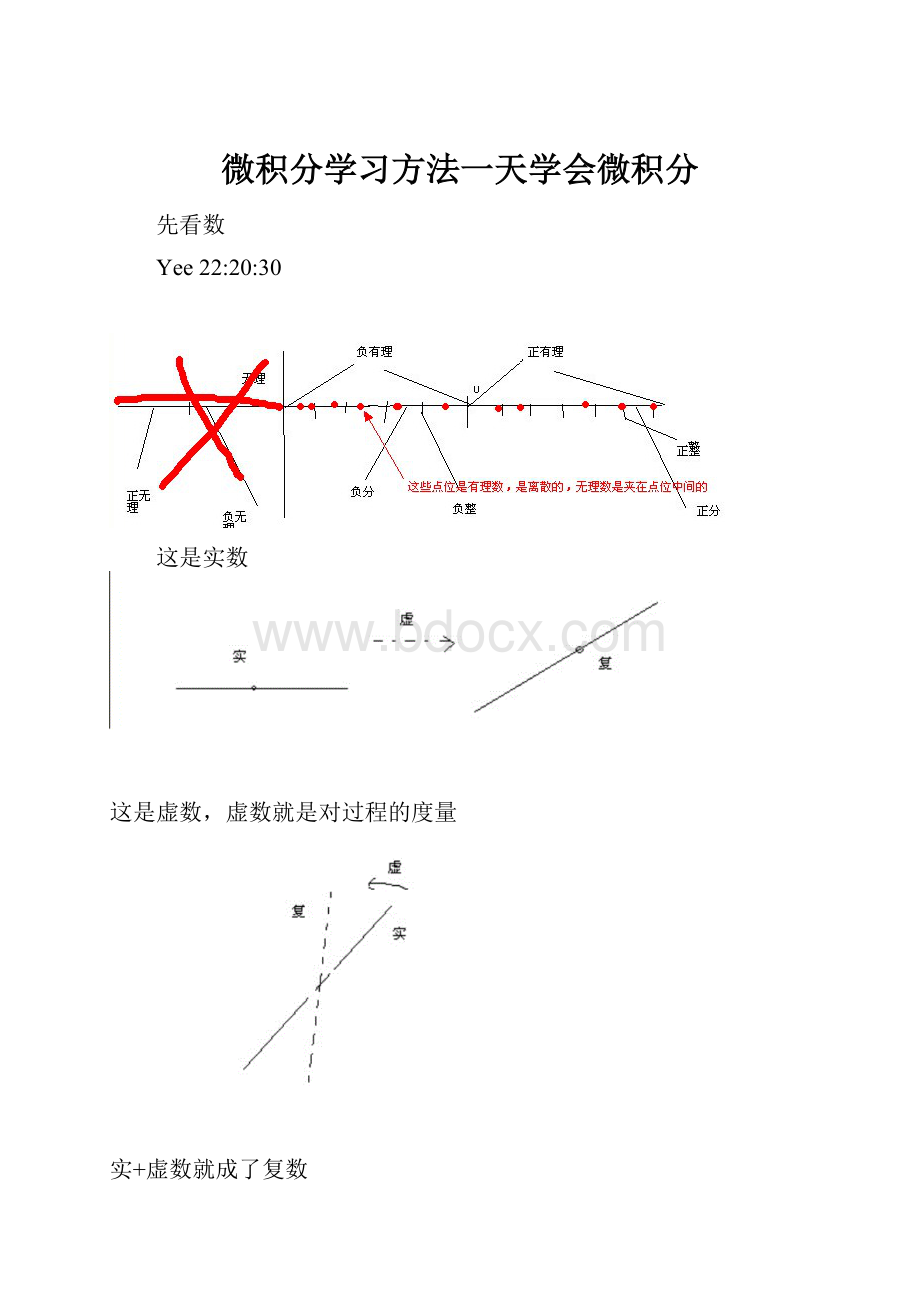
这是实数

这是虚数，虚数就是对过程的度量

实+虚数就成了复数

这是狭义数，就是四维空间以内的

广义数，就是物理上要用到的

进入广义了，和爱的广义相对论对应

它是描述空间里的事情的，所以会有方向

（想象一个线，在空间内穿梭）

狭义的虚数和广义的张量，都是一回事

这二个比较难理解，因为涉及到一个重点

方程=变化（数）

方程就是人们说的规则规则=函数（上面说的那些数）这就是方程了

还有个重点，数之外还有“自然规则”如派，e,i这些，这些就是人们说的自然规律

再看一个图，你就明白了

你看看，这些东西，像环域群

一般也只有一些数学家搞,张量这些玩艺，也只有物理学家才用，就这么简单

你先有这概念，后来你就懂了,数学就是从点到面到空间

这句是重点，后面那些都是为了在空间里描述

打个比方

刚才是数，再说运算

到运算了

数+运算=算术

算术就是数学

你想象一下金箍棒

能长能短，这个变化，也要用数学形容，所以有+-

一个面，能扩展能收缩用数学形容，这是X%

这里就出来问题了

左边的好求

面积，右边的如何求？

只能这样求

用很多“规矩”的形状去填

后来，发现，其实这个问题可以转化为一个简单的问题

“数学都是降维度来处理问题的”

简化后，其实就是解决一个问题

如何用直线去“接近”曲线

如右边的，它可以分成很多很小的段,这个段越小，越精确

这就是微分,就是用线去模拟曲线

线性问题，到非线性问题

你想象用一个无限接受的规矩的方块（可能无数个）

去填一个不规矩的形状，就是积分,这是线与面二个层面的关系

这种其实就是解决非线性问题

非线性问题的解决工具就是微积分，就是东西不平滑了，如何计算的问题

左边是线性，右边是非线性

其实非线性就是函数

函数=变化

这个不平滑的其实就是曲线，曲线就是函数

无非是多几个函数

为了把刚才那个问题，数学化

蓝线是一个曲线

微分就是去用直线来模拟

设这个直线为f（x）这个很小很小很小的模拟段长度为h那么，其实

f（x）到f（x+h）的变化就是曲线的变化

它至少能够反映曲线的平滑程度，你想象一下

就像用一根火柴沿着园边缘滑动

越陡，说明它的变化越大，即曲线越不平滑

告诉你一个简单的理解方式

其实，每个数学名称是符合一点意思的

你可以按中文理解就成了

微分，就是很小的分

积分，当然就是把面积很小的堆在一起，和+-一样对，它能解决物理问题

因为物理很多不是“平整”的，它可能是变化的

所以不学微积分，思维会有局限，只知道整数，和线性变化

，互为逆远算

童心发作22:

55:

33

所以你说八卦是微积分那我就理解你的想法了……

Yee22:

55:

53

你后面会理解的，八挂比这个高级多了

你刚才问了一个问题

估计你没忘，关于方程的

其实方程就是一个变化规律的总结

这个好理解

但是你想过，这个变化的规律也可能有规律么？

这是二个层面

数学上的“元”这个名词就是形容这个层次的

一元就是变化

二元就是变化的变化

所以刚才那个微分的过程，就是无限小分的过程，其实这个过程也是一个变化的过程,

有些拗口，但这个好理解

变化，变化的变化

OK，这就是多元微分了

所以不学多元微分的，不知道变化的变化是可以描述的

从微积分往上推二级

如：

变化->变化的变化

就到多元微分了

以“二”为界

因为，变化的变化的变化的变化的变化，其实都可以简化为

某个变化->某个变化的变化这就是父子关系到

关系

数学里不超过2级的

6级也只能化成2

刚才是文字版的

书上讲的，就是把这个过程“数学化”，其实也挺简单

不会超过+-X%

所有需要用到的“描述”，不是神学，刚才说的在四维空间内已经完备了

你超不过这个系的

还有个导数的概念,刚才微积分已经讲完了

其实就是这点东西

大学扯了一大堆，其实是没有从上往下看

刚才先说数，是想你有一个框架的概念，跳不出四维空间的，那些东西

再来个实际点的干货

进入数学描述

微分

所谓微分，即函数微小变化的规律。

一元微分

如果一个函数变化的规律能够线性归纳，即：

函数=线性变化+高阶无穷小

那么这个函数可微。

f（dx）=Adx+o（dx）（A为一个线性方程，dx为变化量,o为一个阶度）

一元微分，即是对函数的一阶归纳。

定义

x的微分dx

函数在x点的微分：

dy=2xdx

函数的导数为：

dy/dx=2x=f'（x）

求解过程

f（x）=x^2

f'（x）=（x+dx）^2-x^2

=x^2+2xdx+dx^2-x^2

=2x

结果:

函数变化量：

f（x）=（x+dx）^2-（x）^2=2x.dx+dx^2

线性函数：

A=2x

高阶无穷小的量：

o（dx）=dx^2

函数在x点的微分：

dy=2xdx

函数的导数为：

dy/dx=2x=f'（x）

这段你先看一会

这是一元微分，多元的，你理解了变化的变化，自己都能推出来了

先看一下，我一会讲

大学里是这么讲的

看着晕，来个Wiki的

国际版的好理解

你想象一下，如何去用一个“直线（线性）”来模拟“曲线（非线性）”

就是用一个直线去帖着它的边

蓝线就是这个去帖上去的直线

这个就比

这个要帖得紧

你再想一下，如果这个

的长度足够短（短到极限）是不是就是重合了？

这个理解是重点

结合一下那个坐标

如果这个直线在一个足够短的时候和曲线基本重合了，它就“约等于”这个曲线的一个小段了

三角叫delta是表示一个“变化的段”

先别管那个d

容易掉进去，先理解上面的

上面那个图说简单点就是：

x变化了

的时候，y变化了

这是针对那个直线而言的

别看那个曲线先

x变化了

的时候，y变化了

这是直线的变化描述

有点误差，==

应该是：

x变化了

的时候，y变化了

（针对曲线的变化）\

的时候，y变化了dy（针对直线的变化）

上面的理解么

曲线和直线在同样一段x变化的时候，是不同的

再说通俗点

的时候，y变化了

（针对曲线的变化）

这是曲线的变化，一个非线性问题

的时候，y变化了dy（针对直线的变化）

这是直线的变化，一个线性问题

好，用一个最简单的方法讲

这个非常好理解

你带着这个思路去

理解刚才说那个变化的变化理解么

变化也是有规律的

OK

变化是函数吧？

函数其实就是X与Y的方程

最简单的理解

就是x变了，y变

y=2x

这种

一个变量产生，同一条线上的另一个必须根据这个改变

对

因果

就是，X变化了一段，y也变化了一段

这个好理解吧？

精采的就是这里

这个X变化了一段它就是一个量

设y=2x为a

那么

b=2a其实就是描述这个变化的变化

就是方程的方程

你设这个变化为dx

那么变化的过程如何能够变成

y=某玩艺*dx+一个无限小的量

（上面就是微分的数学形式了）

这个某玩艺是一个线性方程（就是坐标系里是一个平整的线）

线性方程（几何表现就是平整的线，不弯的）*这个变化

就是微分干的活了

它把变化当成量计算了

这个是直线

直线里，X变了一段，Y是不是变了一段？

这个是曲线，

微分假设

它变化了dx（这是假设的，不要管它是什么）

y变化了dy

它把这个“变化”又建了一个方程

就是对“变化”设了一个方程，所以他把这个曲线变化的过程把他又可以放在坐标系里来研究了、

这就是对”变化“求解的含义

说白了，变化（量）就是函数

变化（变化）它也是函数把变化当量来计算就是微积分干的活

主要是理解，它把变化当一个量了

我举几个形象的例子

就是管它三七二十一，不管这个变化是什么，把它当一个数

这样就能对变化进行规律总结了

那个d就是新发明的符号，指的就是变化

看这个图

这个变化在已有的知识里，是用

形容的

高中都有

是曲线的变化这个好理解么？

dy是直线的变化

来个干货，说不定好理解

f（x）=x^2这是个方程

好理解吧？

f=function

这是数学表达方式

f（变化的量）=变化的量的表达式

^就是阶

因为你打不出x的平方（你输不出来）

后来人家想了个方法，用^代表了

这样,==来个简单的

y=x^2

y2=（x+dx）^2-x^2

不用管它是什么，它就是

（x+dx）^2-x^2，这里为何要减

你没发现，前面其实就是

（x的变化量）^2-x^2么

这个变化后的值减去变化前的值，是不是就是变化的值？

这主浊变化的变化的值嘛

就是

按这样的顺序

y=x^2是不是一个曲线

是啊

黑的就是y=x^2了

如何知道，它变化了一段后，这个长度是多少？

像这个图，以前是求绿线（直线），你当然好求

但是现在换成了曲线，你知道，这个曲线在这段变化的量是多少？

你应该会想到，它其实在每个变化点都是不一样的

紫线处和红线处变化的就不同

所以它不能用一个很舒服的方程表示，只能求一个近邻

求一个大约

红线的变化，和绿线的变化不是一样的

只能假设这个变化为一个量dx

这个时候y变化了dy，其实就是假设的

微分就是找“x变化了一段“的时候"y变化了多少？

“

就直接按数学方式也许也可以理解

微分就是找“x变化了一段“的时候"y变化了多少？

“

这个要理解

你马上就会理解了

这个图

现在微分就是需要知道黑线那个曲线在x变化时,y是如何变化的（其实y就是变化量）

y=表达式，y就是变化的结果

你假设这个变化为三角x

代进去其实就是已经建立了微分的表达式了

后面就是求

y=x^2

y2=（x+dx）^2-x^2

求上面的微分，就是下面的方式

假设变化了dx代进去一减，这个变化的量就出来了

刚才那个理解，估计有点难

就直接理解

我随便找的，红的和蓝的都不要看

只关注那个黑的

黑线在下面的X变化的，y的变化我标出来了

就是要象形

==我画个干净点的图

看到那个曲线了么，那就是要解决的问题

现在要解决的是：

“知道X变化时Y是如何变化的）

这就么简单

y是曲线在y轴上的投影响，（这儿用数学理解）

这儿要象形结合数轴理解

数轴发现出来就是把东西几何化

其实变化都可以反映在数轴上，其实就是X变化，Y是如何变化的

方程其实就是对变化的过程总结

方程又可以放在坐轴系里

这是规律（代数）问题->几何化的一种方式

说实际点

你做你那永动机

他有些变化，可以总结成方程吧？

这个方程，如果可以画出来，它不一定是直线的

是这样的吧

一定不是

那玩意怪异

现在有个要命的问题

你如何知道，在一段时间，它变化了多少？

现在要你给出来

你如何做这个过程？

比如这么个玩艺

它可能是“电”在“磁”的变化下的规律（你总结出来的方程）

我现在想知道，电变化了一段，磁变化了多少？

如果是简单的如，速度变化，vt=s这个

就好求

这个s=vt其实就是变化的量=一个常量X一个变化的量

这就是个线性问题，它画出来也是个直线

如果是s=vt*ab*ac啥的，他如果能总结出来，就是上面那个玩艺，曲线，这叫非线性问题

t=时间v=速度s=距离

这是最简单的线性问题

速度不变

如果速度是变化的呢

它就成曲线了

要你求变速（瞎动）的物体在一个时间内运动的距离你如何求？

最后描几个点，它成了这么一个玩艺，它是一个方程。

现在看这个图，它在X的变化的时候，Y的变化，就是这个变化的量

这么将一个实际的问题->方程化->几何化了

然后用最简单的方式……

结束

THANKS!

!

!

致力为企业和个人提供合同协议，策划案计划书，学习课件等等

打造全网一站式需求

欢迎您的下载，资料仅供参考