《计算机组成与系统结构》课后习题答案清华大学出版社袁春风主编.docx

《计算机组成与系统结构》课后习题答案清华大学出版社袁春风主编.docx

《《计算机组成与系统结构》课后习题答案清华大学出版社袁春风主编.docx》由会员分享，可在线阅读，更多相关《《计算机组成与系统结构》课后习题答案清华大学出版社袁春风主编.docx（118页珍藏版）》请在冰豆网上搜索。

《计算机组成与系统结构》课后习题答案清华大学出版社袁春风主编

第1章习题答案

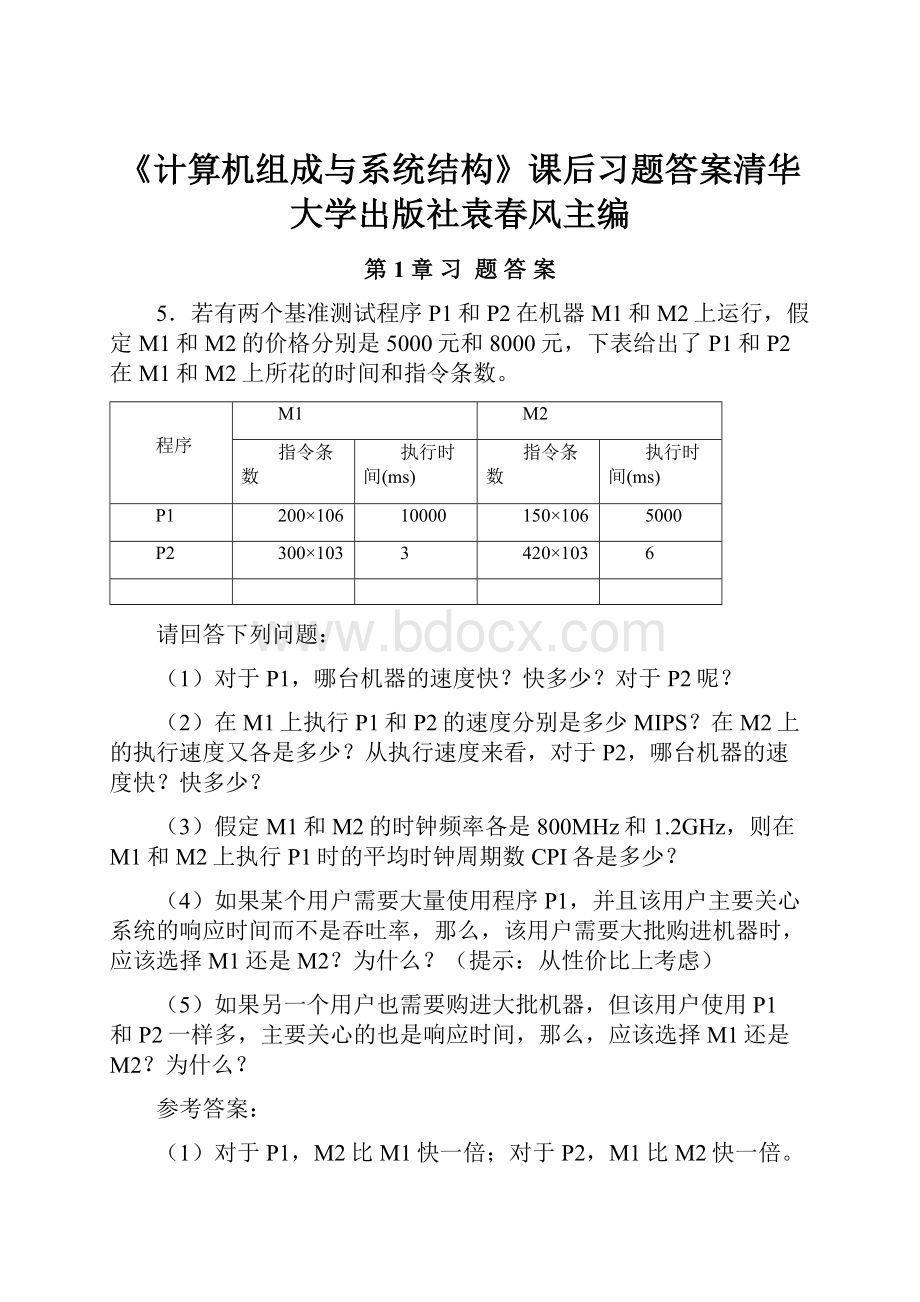
5．若有两个基准测试程序P1和P2在机器M1和M2上运行，假定M1和M2的价格分别是5000元和8000元，下表给出了P1和P2在M1和M2上所花的时间和指令条数。

程序

M1

M2

指令条数

执行时间（ms）

指令条数

执行时间（ms）

P1

200×106

10000

150×106

5000

P2

300×103

3

420×103

6

请回答下列问题：

（1）对于P1，哪台机器的速度快？

快多少？

对于P2呢？

（2）在M1上执行P1和P2的速度分别是多少MIPS？

在M2上的执行速度又各是多少？

从执行速度来看，对于P2，哪台机器的速度快？

快多少？

（3）假定M1和M2的时钟频率各是800MHz和1.2GHz，则在M1和M2上执行P1时的平均时钟周期数CPI各是多少？

（4）如果某个用户需要大量使用程序P1，并且该用户主要关心系统的响应时间而不是吞吐率，那么，该用户需要大批购进机器时，应该选择M1还是M2？

为什么？

（提示：

从性价比上考虑）

（5）如果另一个用户也需要购进大批机器，但该用户使用P1和P2一样多，主要关心的也是响应时间，那么，应该选择M1还是M2？

为什么？

参考答案：

（1）对于P1，M2比M1快一倍；对于P2，M1比M2快一倍。

（2）对于M1，P1的速度为：

200M/10=20MIPS；P2为300k/0.003=100MIPS。

对于M2，P1的速度为：

150M/5=30MIPS；P2为420k/0.006=70MIPS。

从执行速度来看，对于P2，因为100/70=1.43倍，所以M1比M2快0.43倍。

（3）在M1上执行P1时的平均时钟周期数CPI为：

10×800M/（200×106）=40。

在M2上执行P1时的平均时钟周期数CPI为：

5×1.2G/（150×106）=40。

（4）考虑运行P1时M1和M2的性价比，因为该用户主要关心系统的响应时间，所以性价比中的性能应考虑执行时间，其性能为执行时间的倒数。

故性价比R为：

R=1/（执行时间×价格）

R越大说明性价比越高，也即，“执行时间×价格”的值越小，则性价比越高。

因为10×5000>5×8000，所以，M2的性价比高。

应选择M2。

（5）P1和P2需要同等考虑，性能有多种方式：

执行时间总和、算术平均、几何平均。

若用算术平均方式，则：

因为（10+0.003）/2×5000>（5+0.006）/2×8000，所以M2的性价比高，应选择M2。

若用几何平均方式，则：

因为sqrt（10×0.003）×5000

6．若机器M1和M2具有相同的指令集，其时钟频率分别为1GHz和1.5GHz。

在指令集中有五种不同类型的指令A~E。

下表给出了在M1和M2上每类指令的平均时钟周期数CPI。

机器

A

B

C

D

E

M1

1

2

2

3

4

M2

2

2

4

5

6

请回答下列问题：

（1）M1和M2的峰值MIPS各是多少？

（2）假定某程序P的指令序列中，五类指令具有完全相同的指令条数，则程序P在M1和M2上运行时，哪台机器更快？

快多少？

在M1和M2上执行程序P时的平均时钟周期数CPI各是多少？

参考答案：

（1）M1上可以选择一段都是A类指令组成的程序，其峰值MIPS为1000MIPS。

M2上可以选择一段A和B类指令组成的程序，其峰值MIPS为1500/2=750MIPS。

（2）5类指令具有完全相同的指令条数，所以各占20%。

在M1和M2上执行程序P时的平均时钟周期数CPI分别为：

M1：

20%×（1+2+2+3+4）=0.2×12=2.4

M2：

20%×（2+2+4+5+6）=0.2×19=3.8

假设程序P的指令条数为N，则在M1和M2上的执行时间分别为：

M1：

2.4×N×1/1G=2.4N（ns）

M2：

3.8×N×1/1.5G=2.53N（ns）

M1执行P的速度更快，每条指令平均快0.13ns，也即M1比M2快0.13/2.53×100%≈5%。

（思考：

如果说程序P在M1上执行比M2上快（3.8–2.4）/3.8×100%=36.8%，那么，这个结论显然是错误的。

请问错在什么地方？

）

7．假设同一套指令集用不同的方法设计了两种机器M1和M2。

机器M1的时钟周期为0.8ns，机器M2的时钟周期为1.2ns。

某个程序P在机器M1上运行时的CPI为4，在M2上的CPI为2。

对于程序P来说，哪台机器的执行速度更快？

快多少？

参考答案：

假设程序P的指令条数为N，则在M1和M2上的执行时间分别为：

M1：

4N×0.8=3.2N（ns）

M2：

2N×1.2=2.4N（ns）

所以，M2执行P的速度更快，每条指令平均快0.8ns，比M1快0.8/3.2×100%=25%。

8．假设某机器M的时钟频率为4GHz，用户程序P在M上的指令条数为8×109，其CPI为1.25，则P在M上的执行时间是多少？

若在机器M上从程序P开始启动到执行结束所需的时间是4秒，则P占用的CPU时间的百分比是多少？

参考答案：

程序P在M上的执行时间为：

1.25×8×109×1/4G=2.5s，从启动P执行开始到执行结束的总时间为4秒，其中2.5秒是P在CPU上真正的执行时间，其他时间可能执行操作系统程序或其他用户程序。

程序P占用的CPU时间的百分比为：

2.5/4=62.5%。

9．假定某编译器对某段高级语言程序编译生成两种不同的指令序列S1和S2，在时钟频率为500MHz的机器M上运行，目标指令序列中用到的指令类型有A、B、C和D四类。

四类指令在M上的CPI和两个指令序列所用的各类指令条数如下表所示。

A

B

C

D

各指令的CPI

1

2

3

4

S1的指令条数

5

2

2

1

S2的指令条数

1

1

1

5

请问：

S1和S2各有多少条指令？

CPI各为多少？

所含的时钟周期数各为多少？

执行时间各为多少？

参考答案：

S1有10条指令，CPI为（5×1+2×2+2×3+1×4）/10=1.9,所含的时钟周期数为10×1.9=19，执行时间为19/500M=38ns。

S2有8条指令，CPI为（1×1+1×2+1×3+5×4）/8=3.25,所含的时钟周期数为8×3.25=26，执行时间为26/500M=52ns。

（注：

从上述结果来看，对于同一个高级语言源程序，在同一台机器上所生成的目标程序不同，其执行时间可能不同，而且，并不是指令条数少的目标程序执行时间就一定少。

）

10．假定机器M的时钟频率为1.2GHz，某程序P在机器M上的执行时间为12秒钟。

对P优化时，将其所有的乘4指令都换成了一条左移2位的指令，得到优化后的程序P’。

已知在M上乘法指令的CPI为5，左移指令的CPI为2，P的执行时间是P’执行时间的1.2倍，则P中有多少条乘法指令被替换成了左移指令被执行？

参考答案：

显然，P’的执行时间为10秒，因此，P比P’多花了2秒钟，因此，执行时被换成左移指令的乘法指令的条数为1.2G×2/（5–2）=800M。

第二章习题答案

3．实现下列各数的转换。

（1）（25.8125）10=（?

）2=（?

）8=（?

）16

（2）（101101.011）2=（?

）10=（?

）8=（?

）16=（?

）8421

（3）（010110010110.0011）8421=（?

）10=（?

）2=（?

）16

（4）（4E.C）16=（?

）10=（?

）2

参考答案：

（1）（25.8125）10=（11001.1101）2=（31.64）8=（19.D）16

（2）（101101.011）2=（45.375）10=（55.3）8=（2D.6）16=（01000101.001101110101）8421

（3）（010110010110.0011）8421=（596.3）10=（1001010100.010*********…）2=（254.4CCC…）16

（4）（4E.C）16=（78.75）10=（01001110.11）2

4．假定机器数为8位（1位符号，7位数值），写出下列各二进制数的原码和补码表示。

+0.1001，–0.1001，+1.0，–1.0，+0.010100，–0.010100，+0，–0

参考答案：

原码补码

+0.1001：

0.10010000.1001000

–0.1001：

1.10010001.0111000

+1.0：

溢出溢出

–1.0：

溢出1.0000000

+0.010100：

0.01010000.0101000

–0.010100：

1.01010001.1011000

+0：

0.00000000.0000000

–0：

1.00000000.0000000

5．假定机器数为8位（1位符号，7位数值），写出下列各二进制数的补码和移码表示。

+1001，–1001，+1，–1，+10100，–10100，+0，–0

参考答案：

移码补码

+1001：

1000100100001001

–1001：

0111011111110111

+1：

1000000100000001

–1：

01111111111111111

+10100：

1001010000010100

–10100：

0110110011101100

+0：

1000000000000000

–0：

1000000000000000

6．已知[x]补，求x

（1）[x]补=1.1100111

（2）[x]补=10000000

（3）[x]补=0.1010010（4）[x]补=11010011

参考答案：

（1）[x]补=1.1100111x=–0.0011001B

（2）[x]补=10000000x=–10000000B=–128

（3）[x]补=0.1010010x=+0.101001B

（4）[x]补=11010011x=–101101B=–45

7．假定一台32位字长的机器中带符号整数用补码表示，浮点数用IEEE754标准表示，寄存器R1和R2的内容分别为R1：

0000108BH，R2：

8080108BH。

不同指令对寄存器进行不同的操作，因而，不同指令执行时寄存器内容对应的真值不同。

假定执行下列运算指令时，操作数为寄存器R1和R2的内容，则R1和R2中操作数的真值分别为多少？

（1）无符号数加法指令

（2）带符号整数乘法指令

（3）单精度浮点数减法指令

参考答案：

R1=0000108BH=00000000000000000001000010001011b

R2=8080108BH=10000000100000000001000010001011b

（1）对于无符号数加法指令，R1和R2中是操作数的无符号数表示，因此，其真值分别为R1：

108BH,R2：

8080108BH。

（2）对于带符号整数乘法指令，R1和R2中是操作数的带符号整数补码表示，由最高位可知，R1为正数，R2为负数。

R1的真值为+108BH,R2的真值为–（01111111011111111110111101110100b+1b）=–7F7FEF75H。

（3）对于单精度浮点数减法指令，R1和R2中是操作数的IEEE754单精度浮点数表示。

在IEEE754标准中，单精度浮点数的位数为32位，其中包含1位符号位，8位阶码，23位尾数。

由R1中的内容可知，其符号位为0，表示其为正数，阶码为00000000，尾数部分为00000000001000010001011，故其为非规格化浮点数，指数为–126，尾数中没有隐藏的1，用十六进制表示尾数为+0.002116H，故R1表示的真值为+0.002116H×10-126。

由R2中的内容可知，其符号位为1，表示其为负数，阶码为00000001，尾数部分为00000000001000010001011，故其为规格化浮点数，指数为1–127=–126，尾数中有隐藏的1，用十六进制表示尾数为–1.002116H，故R2表示的真值为–1.002116H×10-126

8．假定机器M的字长为32位，用补码表示带符号整数。

下表第一列给出了在机器M上执行的C语言程序中的关系表达式，请参照已有的表栏内容完成表中后三栏内容的填写。

关系表达式

运算类型

结果

说明

0==0U

–1<0

–1<0U

2147483647>–2147483647–1

2147483647U>–2147483647–1

2147483647>（int）2147483648U

–1>–2

（unsigned）–1>–2

无符号整数

有符号整数

无符号整数

有符号整数

无符号整数

有符号整数

有符号整数

无符号整数

1

1

0

1

0

1

1

1

00…0B=00…0B

11…1B（–1）<00…0B（0）

11…1B（232–1）>00…0B（0）

011…1B（231–1）>100…0B（–231）

011…1B（231–1）<100…0B（231）

011…1B（231–1）>100…0B（–231）

11…1B（–1）>11…10B（–2）

11…1B（232–1）>11…10B（232–2）

9．以下是一个C语言程序，用来计算一个数组a中每个元素的和。

当参数len为0时，返回值应该是0，但是在机器上执行时，却发生了存储器访问异常。

请问这是什么原因造成的，并说明程序应该如何修改。

1floatsum_elements（floata[],unsignedlen）

2{

3inti;

4floatresult=0;

5

6for（i=0;i<=len–1;i++）

7result+=a[i];

8returnresult;

9}

参考答案：

参数len的类型是unsigned，所以，当len=0时，执行len-1的结果为11…1，是最大可表示的无符号数，因而，任何无符号数都比它小，使得循环体被不断执行，引起数组元素的访问越界，发生存储器访问异常。

只要将len声明为int型，或循环的测试条件改为i

10.设某浮点数格式为：

其中，移码的偏置常数为16，补码采用一位符号位，基数为4。

（1）用这种格式表示下列十进制数：

+1.7，–0.12，+19，–1/8。

（2）写出该格式浮点数的表示范围，并与12位定点补码整数表示范围比较。

参考答案：

（假定采用0舍1入法进行舍入）

（1）+1.7=+1.1011001B=0.011011B×41,故阶码为1+16=17=10001B,尾数为+0.011011的补码，即0.011011，所以+1.7表示为010001011011。

–0.12=–0.000111101B=–0.011111B×4–1,故阶码为–1+16=15=01111B,尾数为–0.011111的补码，即1.100001,所以–0.12表示为101111100001。

+19=+10011B=0.010011B×43，故阶码为3+16=19=10011B,尾数为0.010011，所以+19表示为010011010011。

–1/8=–0.125=–0.001B=–0.100000×4–1，阶码为–1+16=15=01111B，尾数为–0.100000的补码，即1.100000，所以–1/8表示为101111100000。

（2）该格式浮点数表示的范围如下。

正数最大值：

0.111111B×411111，即：

0.333×415（≈230≈109）

正数最小值：

0.000001B×400000，即：

0.001×4–16（≈2–34≈10–10）

负数最大值：

–0.000001B×400000，即：

–0.001×4–16

负数最小值：

–1.000000B×411111，即：

–1.000×415

因此，该格式浮点数的数量级在10–10～109之间。

12位定点补码整数的表示范围为：

–211～+（211–1），即：

–2048～2047

由此可见，定点数和浮点数的表示范围相差非常大。

11.下列几种情况所能表示的数的范围是什么？

（1）16位无符号整数

（2）16位原码定点小数

（3）16位补码定点小数

（4）16位补码定点整数

（5）下述格式的浮点数（基数为2，移码的偏置常数为128）

参考答案：

（1）无符号整数：

0～216–1。

（2）原码定点小数：

–（1–2–15）～+（1–2–15）。

（3）补码定点小数：

–1～+（1–2–15）。

（4）补码定点整数：

–32768～+32767。

（5）浮点数：

负数：

–（1–2–7）×2+127～–2–7×2–128。

正数：

+2–135～（1–2–7）×2+127。

12.以IEEE754单精度浮点数格式表示下列十进制数。

+1.75，+19，–1/8，258

参考答案：

+1.75=+1.11B=1.11B×20,故阶码为0+127=01111111B,数符为0，尾数为1.110…0，小数点前为隐藏位，所以+1.7表示为00111111111000000000000000000000，用十六进制表示为3FE00000H。

+19=+10011B=+1.0011B×24，故阶码为4+127=10000011B,数符为0，尾数为1.00110…0，所以+19表示为01000001100110000000000000000000，用十六进制表示为41980000H。

–1/8=–0.125=–0.001B=–1.0×2–3，阶码为–3+127=01111100B，数符为1，尾数为1.0…0，所以–1/8表示为10111110000000000000000000000000，用十六进制表示为BE000000H。

258=100000010B=1.0000001B×28,故阶码为8+127=10000111B,数符为0，尾数为1.0000001，所以258表示为01000011100000010000000000000000，用十六进制表示为43810000H。

13．设一个变量的值为4098，要求分别用32位补码整数和IEEE754单精度浮点格式表示该变量（结果用十六进制表示），并说明哪段二进制序列在两种表示中完全相同，为什么会相同？

参考答案：

4098=+1000000000010B=+1.00000000001×212

32位2-补码形式为：

00000000000000000001000000000010（00001002H）

IEEE754单精度格式为：

01000101100000000001000000000000（45801000H）

粗体部分为除隐藏位外的有效数字，因此，在两种表示中是相同的序列。

14．设一个变量的值为–2147483647，要求分别用32位补码整数和IEEE754单精度浮点格式表示该变量（结果用十六进制表示），并说明哪种表示其值完全精确，哪种表示的是近似值。

参考答案：

–2147483647=–1111111111111111111111111111111B

=–1.111111111111111111111111111111×230

32位2-补码形式为：

10000000000000000000000000000001（80000001H）

IEEE754单精度格式为：

11001110111111111111111111111111（CEFFFFFFH）

32位2-补码形式能表示精确的值，而浮点数表示的是近似值，低位被截断

15．下表给出了有关IEEE754浮点格式表示中一些重要数据的取值，表中已经有最大规格化数的相应内容，要求填入其他浮点数的相应内容。

（注：

表中a代表一个在1到10之间的正纯小数）

项目

阶码

尾数

单精度

双精度

以2的幂次表示的值

以10的幂次表示的值

以2的幂次表示的值

以10的幂次表示的值

0

1

最大规格化数

最小规格化数

最大非规格化数

最小非规格化数

+∞

NaN

00000000

01111111

11111110

00000001

00000000

00000000

11111111

11111111

0….00

0….00

1…11

0….00

1…11

0…01

0….00

非全0

0

1

（2–2–23）×2127

1.0×2–126

（1–2–23）×2–126

2–23×2–126=2–149

–

–

0

1

a×1038

a×10–38

a×10–38

a×10–44

–

–

0

1

（2–2–52）×21023

1.0×2–1022

（1–2–52）×2–1022

2–52×2–1022

–

–

0

1

a×10308

a×10–308

a×10–308

a×10–?

–

–

16．已知下列字符编码：

A=1000001，a=1100001，0=0110000，求E、e、f、7、G、Z、5的7位ACSII码和第一位前加入奇校验位后的8位编码。

参考答案：

E的ASCII码为‘A’+（‘E’–‘A’）=1000001+100=1000101,奇校验位P=0，第一位前加入奇校验位后的8位编码是01000101。

e的ASCII码为‘a’+（‘e’–‘a’）=1100001+100=1100101，奇校验位P=1,第一位前加入奇校验位后的8位编码是11100101。

f的ASCII码为‘a’+（‘f’–‘a’）=110