勒让德函数.docx

勒让德函数.docx

《勒让德函数.docx》由会员分享，可在线阅读，更多相关《勒让德函数.docx（24页珍藏版）》请在冰豆网上搜索。

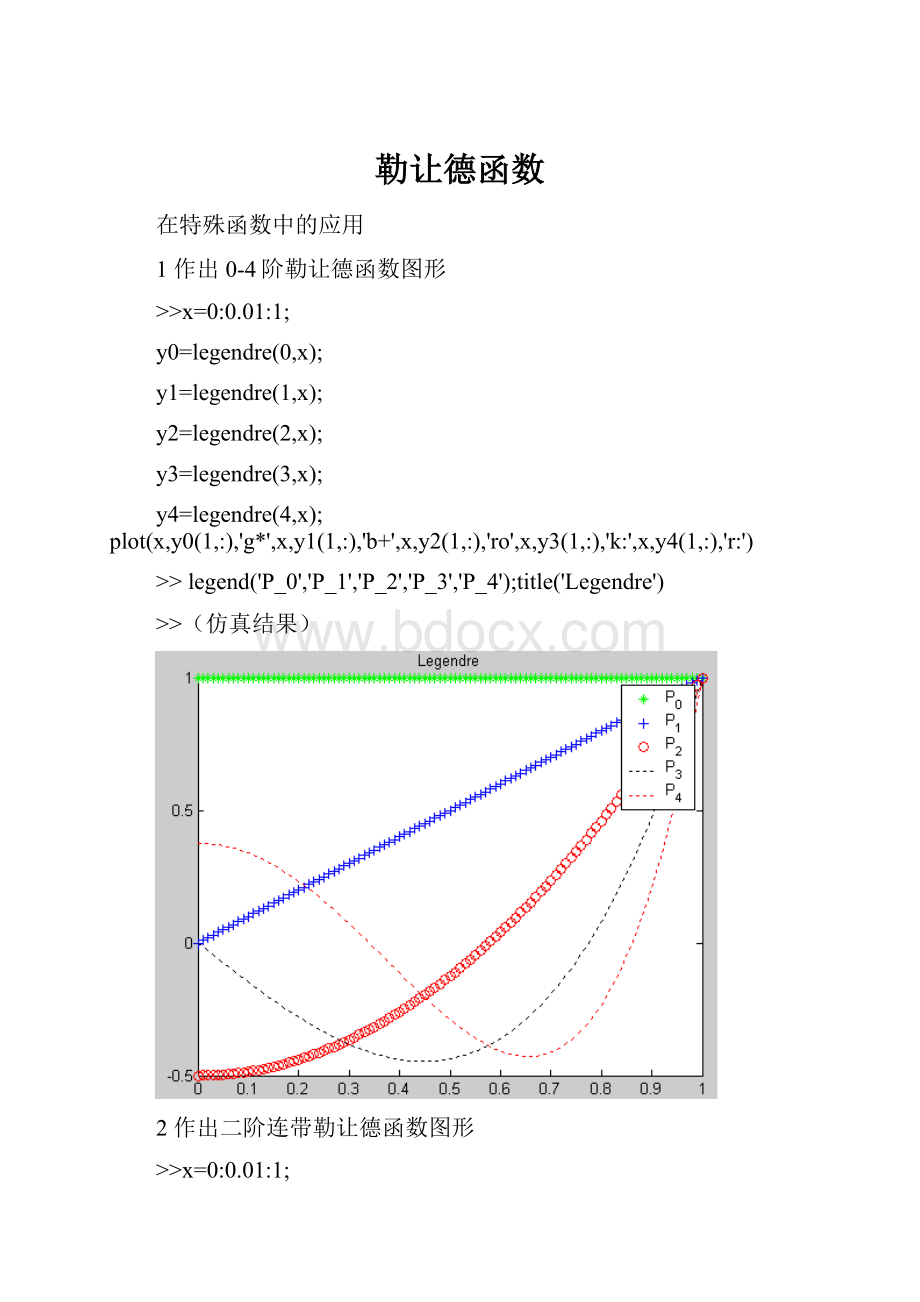
勒让德函数

在特殊函数中的应用

1作出0-4阶勒让德函数图形

>>x=0:

0.01:

1;

y0=legendre（0,x）;

y1=legendre（1,x）;

y2=legendre（2,x）;

y3=legendre（3,x）;

y4=legendre（4,x）;plot（x,y0（1,:

）,'g*',x,y1（1,:

）,'b+',x,y2（1,:

）,'ro',x,y3（1,:

）,'k:

',x,y4（1,:

）,'r:

'）

>>legend（'P_0','P_1','P_2','P_3','P_4'）;title（'Legendre'）

>>（仿真结果）

2作出二阶连带勒让德函数图形

>>x=0:

0.01:

1;

y=legendre（2,x）;

plot（x,y（1,:

）,'g*',x,y（2,:

）,'b+',x,y（3,:

）,'ro'）

>>legend（'P_2^0','P_2^1','P_2^2'）

3作出三阶连带勒让德函数图形

>>x=0:

0.01:

1;

y=legendre（3,x）;

plot（x,y（1,:

）,'g*',x,y（2,:

）,'b+',x,y（3,:

）,'ro',x,y（4,:

）,'k:

'）

>>legend（'P_3^0','P_3^1','P_3^2','P_3^3'）

4作出整数阶贝塞尔函数的图形

>>clear

y=besselj（0:

5,（0:

0.2:

10）'）;

plot（（0:

0.2:

10）',y）

ylabel（'j_v（x）'）

xlabel（'x'）

legend（'J_0','J_1','J_2','J_3','J_4','J_5'）

text（1,0.8,'J_0（x）'）

text（2,0.6,'J_1（x）'）

text（3,0.5,'J_2（x）'）

text（4.2,0.4,'J_3（x）'）

text（5.1,0.4,'J_4（x）'）

>>text（6.5,0.4,'J_5（x）'）

Legendre函数

2007年12月13日星期四01:

00

Legendre函数在解圆平台上电势场时必然遇到的，是在极坐标下考察纬度变量时必然会遇到的。

1.氢原子波函数的角度部分：

用MATLAB来画一画：

l=0,m=0，即s轨道角度部分：

t=0:

0.01:

2*pi;

y0n=legendre（0,cos（t）,'sch'）;

polar（t,y0n（1,:

）.^2）;

l=1,m=0,+1,-1即p轨道角度部分：

t=0:

0.01:

2*pi;

y1n=legendre（1,cos（t）,'sch'）;

polar（t,y1n（1,:

）.^2,'r'）;

holdon;

polar（t,y1n（2,:

）.^2,'g'）;

l=2,m=0,+1,-1,+2,-2即d轨道角度部分：

t=0:

0.01:

2*pi;

y2n=legendre（2,cos（t）,'sch'）;

polar（t,y2n（1,:

）.^2,'r'）;%d（z^2）

holdon;

polar（t,y2n（2,:

）.^2,'g'）;

polar（t,y2n（3,:

）.^2,'b'）;

Legendre多项式

函数

（7.12）

由于展开式

（7.13）

而称为Legendre（勒让德）多项式的母函数。

展开项系数

称为Legendre多项式，下节将证明它满足Legendre方程式（7.11）。

称为阶。

将式（7.13）左边利用二项式定理展开，有

在上式中，含有

的项只出现在含

的项和以前各项中。

在这些项中，将含

的各项展成幂级数，并找出所有含

的项，其系数合为

（7.13）

其中，

这是因为当

时，求和中最低幂项是

，当

时，最低幂项是

。

Legendre多项式的具体形式写成

（7.14）

Legendre多项式的另一微商表达式是Rodrigues（洛德利格）公式

（7.15）

（7.14）式和（7.15）的正确性可以代入Legendre方程式（7.11）直接证明。

由式（7.14）和（7.15）可得出前几阶Legendre多项式具体形式

图7.1显示

在区间〔－1，1〕上的图形，一般有

图7.1Legendre函数

第二类Legendre函数

值得一提的式，Legendre方程（7.11）应有另一个独立的解，这个解称为第二类Legendre函数，记为

。

其形式为

等一般的形式是

由于

的对数形式，第二类Legendre函数在边界

是无界的（并非全部

）。

因此不能构成Legendre方程的本征函数系，所以，对

将不在作讨论。

Legnedre多项式的零点

的零点都是一阶的，全部位于区域〔－1，1〕内。

且

与

的零点相互穿插，在

的两个相邻零点之间必有一个

的零点；反之亦然。

2.3Legnedre多项式的性质

Legendre多项式的性质如下：

递推公式

①

（7.16）

（7.17）

（7.18）

（7.19）

②

（7.20）

对称性

③

（7.21）

特殊点的值

④

（7.22）

⑤

（7.23）

⑥

（7.24）

积分表达形式

⑦

（7.25）

Laplace第一积分

⑧

（7.26）

取

，由式（7.26）得

取

，由式（7.26）得

⑨

（7.27）

Laplace第二积分

⑩

（7.28）

积分公式

（7.29）

（7.30）

（7.31）

利用Rodrigues公式（7.15）可证明积分公式，下面证明方程（7.31）。

利用式（7.15），有

将积分作

次分部积分，然后设

，并利用积分公式

得

下面由母函数入手，证明Legendre多项式得递推公式，将母函数式（7.12）写下

（7.12）

对式（7.12）两边取

导数，得

用

乘上两边，得

将上式左边中母函数再作展开，得等式

（7.32）

比较（7.32）式两边项得系数，得递推关系。

这是式（7.20）的结果。

同理，对式（7.12）两边的求导，得

将上式两边乘以

，并将左边母函数展开，得

（7.33）

比较

项的系数，得

这就是式（7.19）。

其它递推公式可依此导出，这里不再证明。

利用母函数，已证明Legendre式多项式（7.14）满足递推公式（7.16）～（7.20），则式（7.14）是Legendre方程（7.11）的解。

下面证明定理。

定理设函数是

在〔－1，1〕区间上有一、二阶连续倒数的连续函数，

若

满足递推公式（7.16）和式（7.17）～（7.20），则

是Legendre方程

的解。

将递推公式（7.16）两边对

求导，得

（7.34）

再将式（7.16）乘以

，得

（7.35）

将式（7.34）乘以

，并与式（7.35）相加，得

（7.36）

由式（7.17），将

换

成，有

（7.37）

将式（7.37）两边对

求导，得

（7.38）

或写成

（7.39）

将式（7.39）代入式（7.36），得

（7.40）

再由式（7.16）将式（7.40）中的

项替代，最后，得到Legendre方程

2.4Fourier－Legendre级数

第6章§1.3讨论了区间〔－1，1〕上，Legendre方程的本征值为

（7.41）

相应的本征函数是Legendre多项式

（7.42）

由Legendre方程（7.11）知

，

。

在

边界，

因而Legendre方程的解满足自然边界条件，因而有本征函数正交性

（7.43）

第6章§1.4还讨论了函数

在区间〔－1，1〕上用Legendre函数展成的广义Fourier级数，称为Fourier－Lengendre级数。

模计算如下：

将母函数式（7.12）两边平方，得

（7.47）

Fourier－Lengendre级数展开定理

若在区间〔－1，1〕上连续，或有限第一类间断点，那么，Fourier－Lengendre级数

（7.44）

其中

（7.45）

（7.46）

在〔－1，1〕上的连续点收敛于

；在

的间断点，则收敛于平均值

；在

，收敛于

；在

，级数收敛于

。

将方程（7.47）两边对

从－1到1积分，并利用正交关系式（7.43）可知式（7.47）右边的第二项积分等于零。

于是，有

（7.48）

式（7.48）左边的积分可完成为

（7.49）

将式（7.49）与式（7.48）的右边相比较，得

【例7.1】在〔－1，1〕区间上，试求

展成Fourier－Lengendre级数。

解设

根据积分公式（7.30）可知，当

时，所有积分等于零，即

利用式（7.29），计算得

（被积函数是奇函数）

于是有

由上述计算可得出以下结论：

在的Fourier－Lengendre级数中，若是奇数，只含奇数阶Lengendre多项式；若为偶数，只含偶数阶Lengendre多项式。

且Lengendre多项式的阶数最高阶为。

下面列出部分的Fourier－Lengendre多项式的阶数：

2.5具有轴对称性的物理问题举例

由本章§1的讨论可归纳出具有轴对称性的物理问题的形式解。

把对称轴取作求坐标的轴，Helmholtz方程描写的轴对称问题形式解为

（7.50）

Laplace方程描写的轴对称问题的形式解：

（7.51）

对于球内问题，有

对于球外问题，

应为零。

【例7.2】半径为的均匀带电圆环，总电量为

，如图7.2，求圆环周围空间的电势。

图7.2带电的圆环

解先由Coulomb（库仑）定律求在

轴上的电势，

（7.52）

将式（7.52）作Laurant（罗朗）展开，得

（7.53）

势（7.53）可看成是形式解（7.51）在

的边界条件。

比较两式，且有

，得

【例7.3】半径为的半球导体，球面温度保持在，底面温度保持为，如图7.3，求半导体球内的稳定温度分布。

图7.3半圆形导体

解稳定时，导体内的温度分布满足Laplace方程。

温度分部具有轴对称性。

对于球内问题，由式（7.51）有

（7.54）

边界条件是

（7.55）

（7.56）

由式（7.55），有

显然，只有当

为奇数

时才有

。

因而，式（7.54）成为

（7.57）

由式（7.56），有

利用Fourier－Legendre级数展开定理，有

（7.58）

最后一步积分是利用习题7.2第3①题的结果求得的。

将式（7.58）换写成

表达式，并代入式（7.57），有

（7.59）

§3*连带LEGENDRE多项式

3.1连带LEGENDRE多项式

上节讨论了对称的定解问题，当

时，式（7.5）转变成Legendre方程（7.10）。

当物理问题是非轴对称时，

将式（7.5）写下：

（7.59）

类似地，作代换，令

，式（7.5）变成连带Legendre方程

（7.60）

式（7.60）的本征值是

，只有当

取

等整数时，式（7.60）才有本征函数解。

设

（7.61）

于是,有

将上述结果代入式（7.60）得

（7.62）

另则，由Legendre方程（7.11）对

作

次求导，得

（7.63）

比较式（7.63）与（7.62）有

（7.64）

由式（7.61）得到满足方程（7.60）的连带Legendre多项式

（7.65）

在以上推导中，

阶导数表示为

特别是

3.2连带LEGENDRE多项式的性质

积分表达式

①

（7.67）

递推公式

②

（7.68）

③

（7.69）

④

（7.70）

⑤

（7.71）

对称性

⑥

（7.72）

⑦

（7.73）

⑧

（7.74）

正交关系

⑨

（7.75）

⑩

（7.76）

（此文档部分内容来源于网络，如有侵权请告知删除，文档可自行编辑修改内容，供参考，感谢您的配合和支持）