第12讲 一元一次方程的应用一尖子班文档格式.docx

第12讲 一元一次方程的应用一尖子班文档格式.docx

《第12讲 一元一次方程的应用一尖子班文档格式.docx》由会员分享，可在线阅读，更多相关《第12讲 一元一次方程的应用一尖子班文档格式.docx（17页珍藏版）》请在冰豆网上搜索。

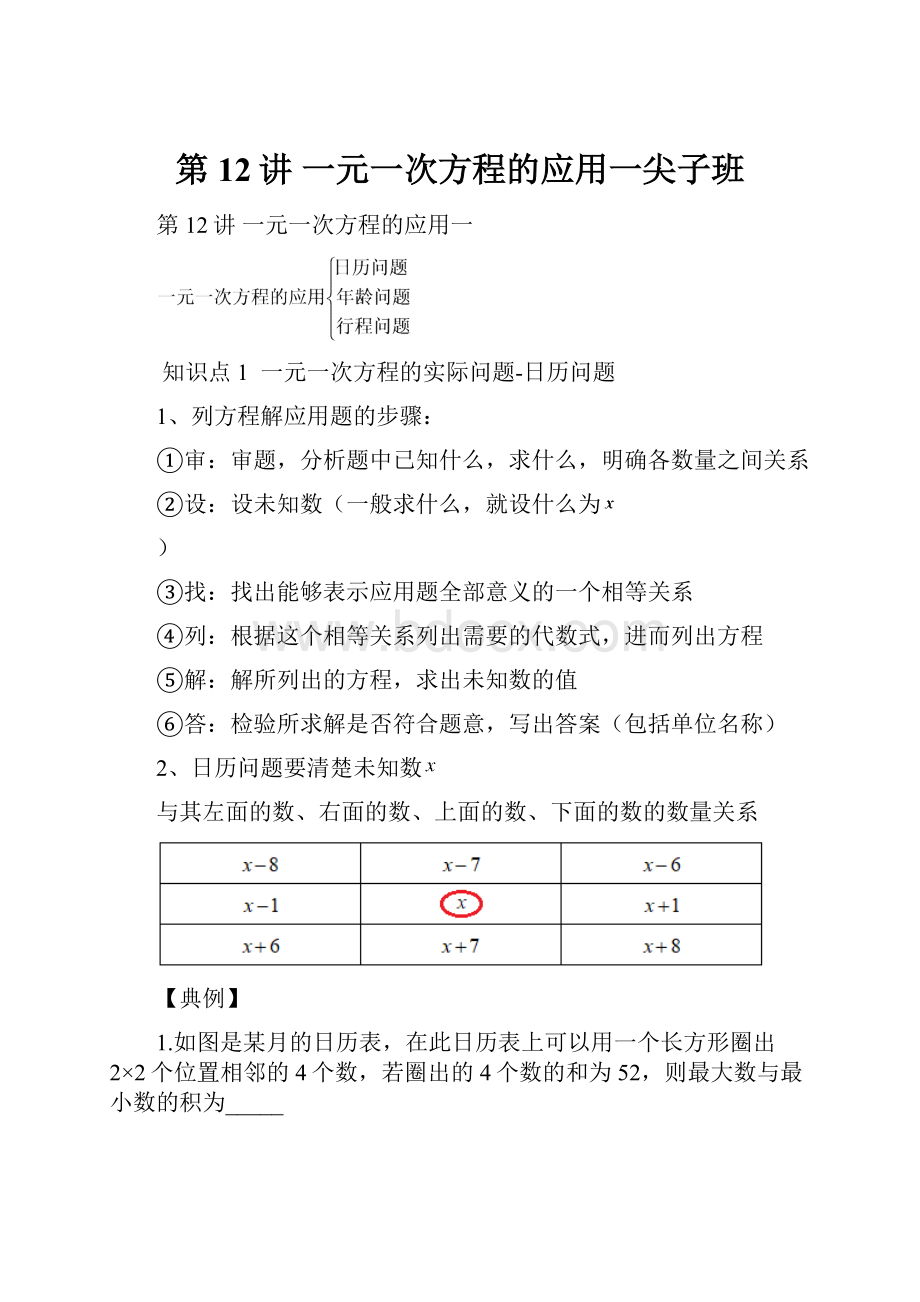
【方法总结】

1、明确各个数在日历中的位置关系，设较简单的数为未知数

2、依据未知数

与其左面的数、右面的数、上面的数、下面的数的关系，表示其他位置的数

【随堂练习】

1．（2017秋•福田区期末）在如图所示的2018年元月份的月历表中，任意框出表中竖列上四个数，这四个数的和可能是（　　）

A．86B．78C．60D．101

【解答】解：

设这四个数中最小的一个数为x，则其余的三个数为x+7，x+14，x+21，

那么，这四个数的和为x+x+7+x+14+x+21=4x+42．

A、如果4x+42=86，那么x=11，不符合题意；

B、如果4x+42=78，那么x=9，符合题意；

C、如果4x+42=60，那么x=4.5，不符合题意；

D、如果4x+42=101，那么x=14.75，不合题意．

故选：

B．

2．（2017秋•南岸区期末）把3的倍数3，6，9，…排成如图所示的数表，用十字形框中表内的五个数，当把十字形上下左右移动，保证每次十字形要框中五个数，则框中的五个数的和不可能是（　　）

A．1680B．1785C．2070D．2100

设十字框中间的数为x，则十字框中的五个数的和：

x+（x﹣15）+（x+15）+（x﹣3）（x+3）=5x，

A、1680÷

5=336，在第二列，不符合题意；

B、1785÷

5=357，在第四列，不符合题意；

C、2070÷

5=414，在第三列，不符合题意；

D、2100÷

5=420，但420不能出现在十字框的中间，所以这五个数的和不能等于2100．符合题意；

D．

3．（2017秋•灵石县期末）如图是某月的日历表，在此日历表上可以用一个矩形圈出3×

3个位置的9个数（如6，7，8，13，14，15，20，21，22）．若用这样的矩形圈圈这张日历表的9个数，则圈出的9个数的和可能为下列数中的（　　）

A．81B．100C．108D．216

设中间的数为x，则左右两边数为x﹣1，x+1，上行邻数为（x﹣7），下行邻数为（x+7），左右上角邻数为（x﹣8），（x﹣6），左右下角邻数为（x+6），（x+8），根据题意得

x+x﹣1+x+1+x﹣7+x+7+x﹣8+x﹣6+x+6+x+8=9x，

则圈出的9个数的和为9的倍数．

观察选项，只有选项A符合题意．

A．

知识点2一元一次方程的实际问题-年龄问题

在年龄问题中，两个人的年龄差始终不变

1.已知：

派派的妈妈和派派今年共36岁，再过5年，派派的妈妈的年龄是派派年龄的4倍还大1岁，当派派的妈妈40岁时，派派的年龄为______岁．

设今年派派的年龄为

岁，则妈妈的年龄为

岁，

根据题意得：

（36﹣x）+5=4（x+5）+1，

解得：

x=4，

所以可得，派派今年4岁，妈妈今年32岁，妈妈与派派的年龄差是28岁

当妈妈40岁时，派派的年龄是40-28=12岁

故答案为：

12．

1、在年龄问题中，两个人的年龄差始终不变

2、看清问题：

是问谁的年龄？

是现在的年龄还是几年前或几年后的年龄？

1．（2018春•东营区校级期中）小明今年12岁，他爷爷今年66岁，____年后，爷爷的年龄是小明的年龄的4倍．

设x年后，爷爷的年龄是小明的年龄的4倍．

66+x=4（12+x），

x=6．

答：

6年后，爷爷的年龄是小明的年龄的4倍．

6．

2．（2017秋•龙湖区期末）小明今年12岁，老师告诉他：

“我今年的年龄是你的3倍小4岁”，接着老师又问小明：

“再过几年我的年龄正好是你的2倍？

”请你帮助小明解决这一问题．

设再过x年老师的年龄正好是小明的2倍，

3×

12﹣4+x=2（12+x），

x=8．

再过8年老师的年龄正好是小明的2倍．

知识点3一元一次方程的实际问题-行程问题

1、基本量、基本数量关系：

路程=速度×

时间

2、相遇问题：

常用的相等关系为：

甲走的路程+乙走的路程=两地距离．

3、追及问题：

寻找相等关系的方法有两种情况，

（1）同地不同时出发：

前者走的路程=追者走的路程；

（2）同时不同地出发：

前者走的路程+两者相距距离=追者走的路程

4、航行问题：

（1）顺水速度=静水速度+水流速度

（2）逆水速度=静水速度-水流速度

5、解题技巧：

要熟练画线形示意图来表示数量关系

1.A、B两地相距3千米，甲从A地出发步行到B地，乙从B地出发步行到A地，两人同时出发，20分钟后相遇，再过10分钟，甲所余路程为乙所余路程的2倍，求两人的速度．

设甲的速度是

千米/分钟，乙的速度是

千米/分钟，由题意得：

所以加的速度是

千米/分钟

乙的速度=

．

甲的速度是

千米/分钟．

1、行程问题：

2、相遇问题，要画线段图来表示和分析数量关系

该题的等量关系为：

甲剩余路程=乙剩余路程×

2，先用总路程、相遇时间表示出俩人的速度，再将各自的速度带入所列的等量关系中。

遇到需要间接表示出来的量找准突破口是关键。

2.已知甲沿周长为300米的环形跑道上按逆时针方向跑步，速度为a米/秒，与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步，速度为3米/秒．设运动时间为t秒．

（1）若a=5，求甲、乙两人第1次相遇的时间；

（2）当t=50时，甲、乙两人第1次相遇，求a的值；

（1）当a=5时，甲的速度为5米/秒，乙的速度为3米/秒，

，是甲追乙，追击路程是（300﹣100）米，速度差是（5﹣3）米/秒，所以

t=（300﹣100）÷

（5﹣3）=100秒．

甲、乙两人第1次相遇的时间是100秒。

（2）当t=50时，甲、乙两人第1次相遇，此时

米/秒，

米/秒

①当

，是甲追乙，追击路程是200米，速度差是（a﹣3）米/秒，可得：

50（a﹣3）=200，

解得a=7；

②当

，是乙追甲，追击路程是100米，速度差是（3﹣a）米/秒，可得：

50（3﹣a）=100，

解得a=1．

甲、乙两人第1次相遇时，a的值是7或1；

1、环形跑道问题，首先判断谁的速度快，速度快的追击速度慢的，由此确定路程差和速度差，即可由“相遇时间=路程差÷

速度差”确定相遇时间。

2、还需注意在环形跑道上，经常出现多次相遇的问题

3.某学生乘船由甲地顺流而下到乙地，然后又逆流而上到丙地，共用3小时，若水流速度为2km/h，船在静水中的速度为8km/h．已知甲、丙两地间的距离为2km，求甲、乙两地间的距离是多少千米？

（注甲、乙、丙三地在同一条直线上）

由题意知：

，所以

，同时对丙的位置需要分类讨论：

（1）丙在甲地和乙地之间，设甲、乙两地距离为

千米，

则

x=12.5．

（2）丙不在甲地和乙地之间，设甲乙两地距离为

x=10．

甲乙两地间的距离为12.5km或10km．

1、解题技巧：

2、解该题的关键是找准等量关系，即甲到乙顺流所用时间+乙到丙逆流所用时间=3

找到等量关系以后带入相关的公式

对于题中丙的位置不确定，解题时要分情况讨论乙、丙的位置与甲、乙位置的关系。

4.有两列火车，客车长200米，每秒行30米，货车长300米，每秒行20米。

（1）两车在平行轨道上齐头同向行进，多少秒后客车超过货车？

（2）如果两车相向而行，从相遇到错车而过，需要多少秒？

（1）由题意得：

速度差=（30-20）米/秒，路程差=客车长=200米

设经过

秒后客车超过货车，列方程得：

（30-20）x=200

解得x=20

两车在平行轨道上齐头同向行进，20秒后客车超过货车.

（2）由题意得：

速度和=（30+20）米/秒，路程和=客车长+货车长=（200+300）米

设从相遇到错车而过，需要

秒，列方程得：

（30+20）y=（200+300）

解得y=10

如果两车相向而行，从相遇到错车而过，需要10秒.

1、在解决火车过定点（或动点）、火车过桥、火车与火车相遇等问题时，需要画线形示意图来表示数量关系，正确找出“路程和（差）”和“速度和（差）”

2、火车过桥常用公式：

火车速度×

时间=车长+桥长

（桥长+列车长）÷

速度=过桥时间；

过桥时间=速度

1．（2017秋•江津区期末）一辆客车，一辆货车和一辆小轿车在同一条直线上朝同一方向行驶，在某一时刻，货车在中，客车在前，小轿车在后，且它们的距离相等，走了15分钟，小轿车追上了货车，又走了5分钟，小轿车追上了客车，问再过_____分钟，货车追上了客车．

设小轿车速度为a，货车速度为b，客车速度为c，某一刻的相等间距为m，则

=15，

=15+5，

化简可得：

15a﹣15b=10a﹣10c，

∴a=3b﹣2c．

设再过t分钟，货车追上客车，

（20+t）（b﹣c）=15（a﹣b），

即：

（20+t）（b﹣c）=15（3b﹣2c﹣b），

t=10．

再过10分钟，货车追上了客车．

10．

2．（2017秋•历下区期末）甲乙两车同时从A地出发，在相距900千米的AB两地间不断往返行驶，知甲车的速度是每小时25千米，乙车的速度是每小时20千米，则经过____小时甲乙两车第二次迎面相遇

设经过x小时甲乙两车第二次迎面相遇，依题意有

（25+20）x=900×

4，

解得x=80．

经过80小时甲乙两车第二次迎面相遇．

80．

3．（2017秋•长兴县期末）如图，已知正方形ABCD的边长为24厘米．甲、乙两动点同时从顶点A出发，甲以2厘米/秒的速度沿正方形的边按顺时针方向移动，乙以4厘米/秒的速度沿正方形的边按逆时针方向移动，每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动，则第四次相遇时甲与最近顶点的距离是　____厘米．

设第1次相遇的时间为x秒，依题意有

（2+4）x=24×

解得x=16；

设第2次相遇的时间为y秒，依题意有

（2+1+4+1）y=24×

解得y=12；

设第3次相遇的时间为z秒，依题意有

（2+1+1+4+1+1）z=24×

解得z=9.6；

设第4次相遇的时间为t秒，依题意有

（2+1+1+1+4+1+1+1）t=24×

解得y=8；

2×

16﹣（2+1）×

12+（2+1+1）×

9.6﹣（2+1+1+1）×

8

=32﹣36+38.4﹣40

=﹣5.6，

故第四次相遇时甲与最近顶点的距离是5.6厘米．

5.6．

4．（2017秋•惠民县期末）我们知道，钟表的时针与分针每隔一定的时间就会重合一次，请利用所学知识确定，时针与分针从上一次重合到下一次重合，间隔的时间是_____小时．

设间隔的时间为x小时，

可得：

（60﹣5）x=60，

x=

即再过

小时时针与分针再次重合，

综合运用

1.小明在日历的某月上圈出五个数，呈十字框形，它们的和是55，则中间的数是？

设中间的数是

，则其它四个数字分别是

x﹣1+x+1+x+x﹣7+x+7=55，

x=11．

则中间的数是11

【难度】易

【结束】

2.小明今年12岁，他爷爷60岁，经过多少年以后，爷爷的年龄是小明的4倍．

设经过

年后，爷爷的年龄是小明的4倍．

60+x=4（12+x）．

解之得x=4．

经过

年后，爷爷的年龄是小明的4倍

3.列方程解应用题

甲、乙两人同时从相距25千米的A地去B地，甲骑车乙步行，甲的速度是乙的速度的3倍，甲到达B地停留40分钟，然后从B地返回A地，在途中遇见乙，这时距他们出发的时间恰好3小时，求两人的速度各是多少？

设乙的速度为x千米/小时，则甲的速度为3x千米/小时，依题意有

解得x=5，

3x=15

甲的速度为15千米/小时，乙的速度为5千米/小时．

4.如图所示，两人沿着边长为90m的正方形，按A→B→C→D→A…的方向行走，甲从A点以65m/min的速度、乙从B点以75m/min的速度行走，当乙第一次追上甲时，将在正方形的那条边上？

设乙x分钟后追上甲，

由题意得，75x﹣65x=270，

x=27，

则乙27分钟后追上甲，此时乙走了75×

27=2025米

因为正方形周长为90×

4=360m

所以2025÷

360=5……225，

当乙从B点出发，走225米后在AD边上

即乙第一次追上甲是在AD边上．

5.一轮船航行于两个码头之间，逆水航行需10小时，顺水航行需6小时，已知该船在静水中每小时航行8千米，则两码头间的距离为多少千米．

设静水的速度为x千米/时，则轮船的顺水速度为（x+8）千米/时，逆水航行速度为（x﹣8）千米/时，由题意，得

6（x+8）=10（x-8），

x=32，

（8+32）×

6=240（千米）．

两码头之间的距离为240千米．

6.在一段铁路上，两列火车相向驶过，若A列火车全长180m，B列火车全长160m，两列火车的错车时间为1.7秒，已知A列车的速度比B火车每秒快5m，则A、B两车的速度分别是？

设B车的速度是

m/s，则A车的速度是

m/s，依题意有

1.7（x+x+5）=180+160，

解得x=97.5，

x+5=102.5．

A、B两车的速度分别是102.5m/秒、97.5m/秒．

7.一个自行车队进行训练，训练时所有队员都以相同的速度前进，突然，1号队员以每小时比其他队员快10千米的速度独自行进，行进了10千米后掉转车头，速度不变往回骑，直到与其他的队员会合．从1号队员离队开始到与其他队员重新会合，经过了15分钟．

（1）其他队员的行进速度是多少？

（2）1号队员从离队开始到与队员重新会合这个过程中，经过多长时间与其他队员相距1千米？

（1）设其他队员的行进速度是

千米/小时，1号队员的速度是（

+10）千米/小时，依题意有：

故其他队员的行进速度是35千米/小时．

（2）设经过y小时长时间与其他队员相距1千米，依题意有

①35y+1=（35+10）y，

；

②35y+（35+10）y=10×

2﹣1，

小时或

小时长时间与其他队员相距1千米．