7年级春季班06同位角内错角同旁内角及平行线的判定教案教学设计导学案Word文件下载.docx

7年级春季班06同位角内错角同旁内角及平行线的判定教案教学设计导学案Word文件下载.docx

《7年级春季班06同位角内错角同旁内角及平行线的判定教案教学设计导学案Word文件下载.docx》由会员分享，可在线阅读，更多相关《7年级春季班06同位角内错角同旁内角及平行线的判定教案教学设计导学案Word文件下载.docx（25页珍藏版）》请在冰豆网上搜索。

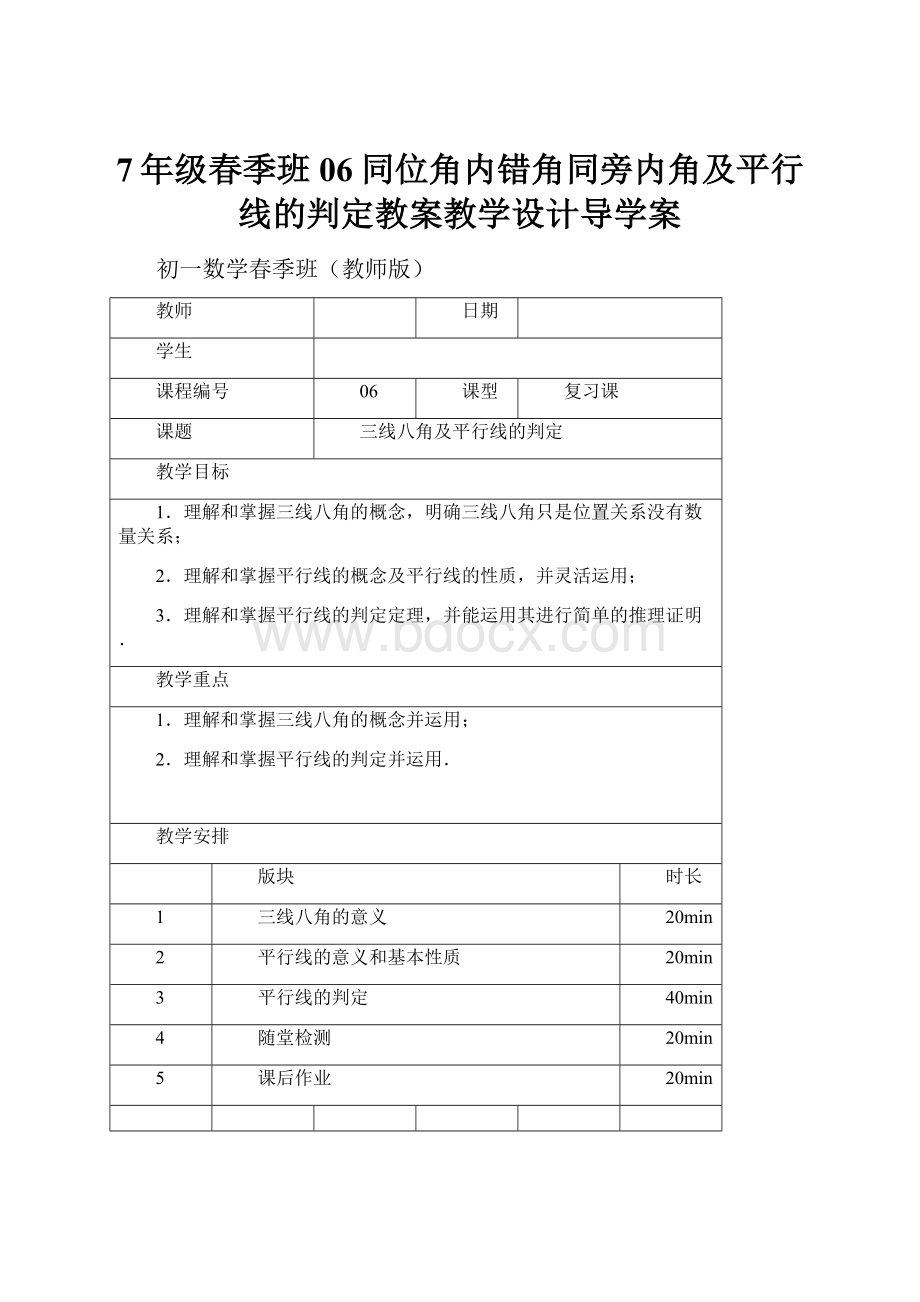
一对角互为同旁内角．（如）

注意：

三线八角是位置关系，数量上没有确定的关系．

【例1】在直线AB、CD被直线EF所截的八个角中∠1和∠5是一对________角，∠3和∠5是一对________角，∠4和∠5是一对________角．

【难度】★

【答案】同位角；

内错角；

同旁内角．

【解析】同位角像字母F，内错角像字母Z，同旁内角像字母U．

【总结】本题考查同位角、内错角、同旁内角的概念及特征．

【例2】

（1）如图∠1和∠2是直线________与________被直线_______所截，所形成的______角；

（2）∠3和∠4是直线_____与_______被直线______所截，所形成的_______角；

（3）∠C的同旁内角是_________．

【答案】

（1）DC、AB、DB、内错角；

（2）AD、CB、DB、内错角；

（3）．

【解析】两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角叫做

内错角，内错角像字母Z，同旁内角像字母U．

【总结】本题考查内错角、同旁内角的概念及特征．

【例3】如图，下列说法错误的是（）

A．∠5和∠3是同位角B．∠1和∠4是同位角

C．∠1和∠2是同旁内角D．∠5和∠6是内错角

【答案】B

【解析】两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做同位角，

故∠1和∠4不是同位角．

【例4】如图，与∠C是同旁内角的有（）

A．5个B．4个C．3个D．2个

【解析】∠C的同旁内角有：

∠CED、∠B、∠EDC、∠ADC共四个．

【总结】本题考查同旁内角的概念及特征．

【例5】如图，同旁内角的对数是（）

A．5对B．4对C．3对D．2对

【难度】★★

【解析】两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的一对角互

为同旁内角．

【例6】如图，∠1和∠2是同位角的是（）

A．

（1）

（2）B．

（2）（3）（4）C．

（1）

（2）（4）D．（3）（4）

【答案】C

【解析】

（1）

（2）（4）中∠1与∠2都在截线的同旁，并且都在被截直线的同侧，是同位角；

（3）中∠1与∠2两边不在同一直线上，不是同位角，故选C．

【总结】本题考查同位角的概念及特征，注意很多学生会容易误以为

（2）中的两个角不是

同位角，老师们要注意纠错哦．

【例7】指出下图中：

（1）∠C与∠D的关系；

（2）∠B与∠GEF的关系；

（3）∠A与∠D的关系；

（4）∠AGE与∠BGE的关系；

（5）∠CFD与∠AFB的关系．

（1）同旁内角；

（2）同位角；

（3）内错角；

（4）邻补角；

（5）对顶角．

【解析】两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做

同位角．两个角分别在截线的两侧，且在两条直线之间，具有这样位置关系的一对角

叫做内错角．两个角都在截线的同一侧，且在两条被截线之间，具有这样位置关系的

一对角互为同旁内角．

【总结】本题考查同位角、内错角、同旁内角、邻补角、对顶角的概念及特征．

【例8】找出图中∠1的所有的同位角．

【答案】∠GEF、∠CBM、∠ADF、∠BCN．

【解析】两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角叫做

同位角．

【总结】本题考查同位角的概念及特征．

【例9】如图

（1）直线DE、BC被直线AB所截，射线DF在∠ADE内部，指出∠1的同

位角；

（2）如果∠1和∠2相等，那么∠1和∠4相等吗?

∠1和∠ADE相等吗?

为什么?

（1）∠ADF、∠ADE；

（2）．

（2）因为∠1=∠2（已知）

所以BC∥DE（内错角相等，两直线平行）

所以∠1=∠ADE（两直线平行，同位角相等）

所以∠1不等于∠4

【总结】本题考查平行线的判定及性质的综合运用．

【例10】三条直线两两相交，且不交于同一点，则在所成的图形中，共有多少对同位角?

多少对内错角?

多少对同旁内角．

【答案】12；

6；

6．

【解析】同位角：

∠1与∠12、∠1与∠6、∠4与∠11、∠4与∠5、∠3与∠8、∠3与∠10、

∠2与∠7、∠2与∠9、∠9与∠6、∠12与∠5、∠11与∠8、∠10与∠7；

内错角：

∠2与∠5、∠4与∠9、∠3与∠6、∠3与∠12、∠10与∠5、∠9与∠8；

同旁内角：

∠2与∠6、∠8与∠10、∠4与∠12、∠3与∠5、∠3与∠9、∠5与∠9．

1、平行线的定义

同一平面内，不相交的两条直线叫平行线．

2、平行线的基本性质

（1）经过直线外一点，有且只有一条直线与已知直线平行；

（2）平行线之间的距离处处相等；

（3）平行于同一条直线的两直线平行（平行的传递性）．

（4）同一平面内，垂直于同一条直线的两直线平行．

（5）两条平行线中，任意一条直线上的所有点到另一条直线的距离是一个定值，这个定值叫做这两条平行线间的距离，平行线间的距离处处相等．

【例11】如图，在长方形ABCD-A1B1C1D1中．CC1_______BC，CC1_______C1D1,

AA1_______DD1，AD_______BC，与AB平行的棱有_________．

【答案】⊥；

⊥；

∥；

棱．

【解析】略

【总结】本题考查平面上直线间的位置关系．

【例12】

（1）在同一平面内，两条不重合的直线有两种位置关系_______和________；

（2）如果两条直线都_______于同一条直线，那么这两条直线平行．

（1）相交、平行；

（2）平行．

（1）同一平面内，不重合的直线要么相交要么平行；

（2）平行于同一条直线的两直线平行．

【总结】本题考查平面上直线间的位置关系及平行线的传递性．

【例13】在同一平面内，和已知直线平行的直线（）

A．有且只有一条B．有无数条C．一条也没有D．条数不确定

【解析】同一平面内和已知直线平行的直线有无数条．

【例14】已知两条直线都垂直于第三条直线，那么这两条直线（）

A．垂直B．平行C．相交D．可能垂直，也可能平行

【答案】D

【解析】同一平面内，垂直于同一条直线的两直线平行，否则可能产生异面垂直．

【例15】判断题：

（1）同位角一定相等（）

（2）不相交的两条直线叫平行线（）

（3）过直线外一点有且只有一条直线和已知直线平行（）

（4）和已知直线平行的直线有无数条（）

（1）×

；

（2）×

（3）√；

（4）√．

（1）只有两直线平行，同位角才相等；

（2）前提是在同一平面内，×

（3）√；

【例16】下列各图中，不能判断直线a∥b的是（）

【解析】A可通过内错角相等判断出平行；

B可以通过同一平面内，垂直于同一条直线的两

直线平行；

D可以通过同位角相等两直线平行来判断．

【总结】本题考查平行线的判定．

【例17】判断题：

（1）在同一平面内，不相交的两条线段是平行线（）

（2）两条直线不相交则必平行（）

（3）与已知直线平行的直线有且只有一条（）

（4）与已知直线垂直的直线有且只有一条（）

（2）×

（3）×

（4）×

．

（1）错，线段有一定长度可以不相交，但其延长线确可能相交，只有两线段的延

长线也不会相交才叫平行线；

（2）前提是在同一平面内，错；

（3）有无数条，×

（4）有无数条，×

【例18】看图填空，并在括号里写出适当的理由．

（1）如图；

因为∠1=__________（已知）

所以AD∥BC（）

（2）因为∠1=∠A（已知）

所以_________∥_________（）

（1）∠2、同位角相等，两直线平行；

（2）AE、CD、同位角相等，两直线平行．

【解析】同位角相等两直线平行．

【例19】如图，如果∠1等于它的余角，∠2的补角是它的3倍，那么AB与CD的关系是（）．

A．垂直B．平行C．相交D．不能确定

【解析】因为∠1=它的余角，所以∠1=45°

，

又因为∠2的补角是它的3倍，所以∠2=45°

所以AB∥CD（内错角相等，两直线平行）

【例20】直线AB、CD、a、b在同一平面内，且AB∥CD，若直线a与AB、CD都相交，直线b与AB、CD也都相交，则直线a、b的位置关系是（）．

A．垂直B．平行C．相交D．相交或平行

【解析】可能相交也可能平行．

【例21】下列四个说法中，正确的个数是（）．

1在同一平面内不相交的两条线段必平行；

2在同一平面内不相交的两条直线必平行；

3在同一平面内不平行的两条线段必相交；

4在同一平面内不平行的两条直线必相交

A．1B．2C．3D．4

【答案】A

【解析】①错：

线段有一定长度可以不相交，但其延长线却可能相交，只有两线段的延长线

也不会相交才叫平行；

②错：

可能重合；

③错：

注意题中说的是“线段”；

④正确．

【总结】本题考查同一平面内直线的位置关系．

【例22】如图，经过点P画直线PE∥OA，交OB于点E；

画直线PF∥OB，交OA于点F．

【答案】见解析．

（1）首先，将三角尺的直角边与直线OA重合，将其中一条

直角边紧靠直尺，并固定直尺；

（2）将三角尺与直线AB重合的直角边沿直尺平行移动至过点P处；

（3）沿着三角尺的直角边画出过点P的直线PE，则直线PE即为所求的平行线．

同理，画出直线PF即可．

【总结】本题考查平行线的作法．

【例23】如图，直线AB、CD相交于点O，P是直线AB、CD外的一点，经过点P画出直线EF，与直线CD相交于点E，与直线AB平行．

（1）首先，将三角尺的直角边与直线AB重合，

将其中一条直角边紧靠直尺，并固定直尺；

（3）沿着三角尺的直角边画出过点P的直线EF，则直线EF即为所求的平行线．

【总结】本题考查平行线的作法，需要三角尺、直尺两个作图工具．

【例24】因为∠1=_________（已知）

所以DE∥_____________（）

因为∠2=_________（已知）

所以EF∥_____________（）

因为∠3+_________=180°

（已知）

所以BC∥_____________（）

【答案】∠B；

BC；

同位角相等，两直线平行；

∠3；

AC；

内错角相等，两直线平行；

∠4；

同旁内角互补，两直线平行；

∠C；

DE；

同位角相等，两直线平行．

【解析】同位角相等，两直线平行；

同旁内角互补，两直线平行．

【例25】在同一平面内有互不重合的五条直线a1、a2、a3、a4、a5，若a1∥a2，a2⊥a3，

a3∥a4，a4⊥a5，那么a1与a5的位置关系是什么．

【难度】★★★

【答案】平行，见解析．

【解析】因为a3∥a4，a4⊥a5，所以a3⊥a5，又因为a2⊥a3，所以a2∥a5．又因为a1∥a2，

所以a1∥a5（平行于同一条直线的两条直线互相平行）．

【总结】本题考查同一平面内，两直线的位置关系．

【例26】直线a、b被直线l所截，如果∠1=∠2，那么a∥b吗？

为什么．

【解析】因为∠1=∠2（已知），

∠2=∠3（对顶角相等）

所以∠1=∠3（等量代换）

所以a∥b（同位角相等，两直线平行）

【例27】直线AB、CD被直线EF所截，H为CD与EF的交点，如果∠1=60°

，∠2=30°

GH⊥CD，垂足为H，说明AB∥CD．

【解析】因为GH⊥CD（已知），所以∠DHG=90°

（垂直的意义）

又因为∠2=30°

（已知），所以∠DHF=60°

（等式性质）

所以∠EHC=60°

（对顶角相等）

因为∠1=60°

（已知），所以∠EHC=∠1=60°

（等量代换）

所以AB∥CD（同位角相等，两直线平行）

【总结】本题考查平行线的判定定理及垂直意义的综合运用．

【例28】已知CD⊥DA，DA⊥AB，∠1=∠2，说明DF∥AE的理由．

【答案】见解析

【解析】因为CD⊥DA，DA⊥AB（已知），所以∠CDA=∠DAB=90°

又因为∠1=∠2（已知），所以∠FDA=∠DAE（角的和差）

所以DF∥AE（内错角相等，两直线平行）

【总结】本题考查平行线的判定定理的运用．

【例29】根据图中已知条件说明AB∥CD的理由．

（1）因为，

（2）60°

的对顶角还是60°

，30°

的余角是60°

，60°

=60°

所以AB∥CD（内错角相等，两直线平行）

（3）因为，所以，

所以∠DCA+∠CAB=180°

，所以AB∥CD（同旁内角互补，两直线平行）

【总结】本题考查平行线的判定定理的综合运用．

【例30】已知，BE、DE分别平分∠ABD、∠CDB，∠E=90°

，判断AB、CD是否平行，请说明理由．

【答案】平行．

【解析】因为∠E=90°

所以∠EBD+∠EDB=90°

（三角形的内角和等于180°

）

又因为BE、DE分别平分∠ABD、∠CDB（已知）

所以∠ABD+∠CDB=2∠EBD+2∠EDB=180°

（角平分线意义）

所以AB∥CD（同旁内角互补，两直线平行）

【习题1】下列说法中，错误的有（）

1∠1与∠2是直线AD、BC被直线AC所截的内错角；

2∠1与∠B是直线AC、BC被直线AB所截得的同旁内角；

3∠3与∠4是直线AC、CD被直线AD所截得的内错角；

4∠2与∠4是直线AD、AC被直线CD所截得的同位角．

A．1个B．2个C．3个D．4个

（1）错误：

应是直线AB、DC被直线AC所截得的内错角；

（2）正确；

（3）正确；

（4）正确．

【总结】本题考查内错角、同位角、同旁内角的概念．

【习题2】两条直线被第三条直线所截，在形成的八个角中，如果∠1与∠2是同位角，∠1与∠3是内错角，那么∠3与∠2是（）．

A．同位角B．同旁内角C．邻补角D．对顶角

【解析】作图即可得出．

【总结】本题考查三线八角中各个角之间的关系．

【习题3】如图，点P在∠AOB的内部，过P点分别作a∥AO，b∥OB．

（1）首先，将三角尺的直角边与直线OA重合，将其中

一条直角边紧靠直尺，并固定直尺；

（2）将三角尺与直线OA重合的直角边沿直尺平行移动至过点P处；

（3）沿着三角尺的直角边画出过点P的直线a，则直线a即为所求的平行线．

同理画出直线b即可．

【总结】本题考查平行线的的作法．

【习题4】如图，已知∠C=∠B，AE平分∠DAC，说明AE∥BC的理由．

【解析】因为∠DAC=∠B+∠C（三角形的一个外角等于和它不相邻的两个内角的和）

又∠DAC=∠DAE+∠EAC（角的和差）

所以∠B+∠C=∠DAE+∠EAC（等量代换）

因为AE平分∠DAC（已知）

所以∠DAE=∠EAC（角平分线的意义）

因为∠C=∠B（已知）

所以∠DAE=∠B（等量代换）

所以AE∥BC（同位角相等，两直线平行）

【总结】本题考查平行线的判定与角平分线意义的综合运用．

【习题5】如图，CE平分∠ACD，∠1=∠B，说明AB∥CE．

【解析】因为CE平分∠ACD（已知）

所以∠1=∠2（角平分线的定义）

又因为∠1=∠B（已知）

所以∠B=∠2（等量代换）

所以AB∥CE（同位角相等，两直线平行）

【总结】本题考查平行线的判定与角平分线的意义的综合运用．

【习题6】如图，完成下列填空：

因为∠1=∠4（已知）

所以AB∥______（）

因为∠2=∠3（已知）

所以_______∥______（）

因为AE⊥BD，CF⊥BD（已知）

所以________∥______（）

【答案】CD；

AD；

AE；

CF；

垂直于同一条直线的两条直线互相平行．

【解析】考查平行线的判定．

【习题7】如图，∠2的同位角，内错角各有几个，请用数字标出．

【解析】同位角的形状如F，图中共有3个；

内错角的形状如Z，图中共有2个．.

【总结】本题考查同位角的概念，老师可以让学生自己先试着标一下．

【习题8】如图，∠1+∠2=180°

，说明BE∥DF的理由．

【答案】略．

【解析】因为∠1+∠3=180°

（平角的定义）

又因为∠1+∠2=180°

（已知）

所以∠2=∠3（等量代换）

所以BE∥DF（同位角相等，两直线平行）

【习题9】如图，已知AD⊥BC，EF⊥BC，∠BEF=∠ADG，试说明DG∥BA．

【解析】因为AD⊥BC，EF⊥BC（已知）

所以EF∥AD（垂直于同一条直线的两条直线互相平行）

所以∠BEF=∠BAD（等量代换）

又因为∠BEF=∠ADG（已知）

所以∠BAD=∠ADG（等量代换）

所以DG∥AB（内错角相等，两直线平行）

【总结】本题考查平行线的性质定理与判定定理的综合运用．

【习题10】∠AOE+∠BEF=180°

，∠AOE+∠CDE=180°

，那么可以判断哪几组直线平行?

并说明理由．

【解析】因为∠BEF=∠OED（对顶角相等）

又因为∠AOE+∠BEF=180°

所以∠AOE+∠OED=180°

所以AO∥DF（同旁内角互补，两直线平行）

所以∠AOE=∠DEB（两直线平行，同位角相等）

又因为∠AOE+∠CDE=180°

（已知）

所以∠CDE+∠DEB=180°

所以CD∥OB（同旁内角互补，两直线平行）

【总结】本题考查平行线的性质定理与判定定理的综合运用，注意认真分析题目中条件．

【作业1】说出图中的同位角、内错角、同旁内角分别是哪几对．（只考虑标了数字的角）

∠1与∠3、∠1与∠5、∠2与∠4、

∠1与∠8、∠3与∠5；

内错角：

∠2与∠7、∠3与∠6、∠5与∠7、∠4与∠8；

同旁内角：

∠1与∠2、∠1与∠6、∠2与∠6、∠3与∠4、

∠3与∠7、∠4与∠7、∠5与∠8、∠1与∠4．

【作业2】同一平面内，A、B为直线l外不同两点，直线a过点A，且a⊥l，直线b过点B，且b⊥l，则a、b的关系是（）．

A．相交B．平行C．垂直D．不能确定

【解析】垂直于同一条直线的两直线平行

【总结】本题考查同一平面内两直线位置关系．

【作业3】下列说法中正确的是（）

A．在同一平面内，两直线的位置关系有相交、平行、垂直三种

B．在同一平面内，不垂直的两条直线平行

C．在同一平面内，不相交的两直线不垂直

D．在同一平面内，不平行的两直线垂直

【解析】A错误：

垂直属于相交的一种特殊情况；

B错误：

不垂直也可以相交；

C正确；

D错误：

不平行的两直线也可以相交．

【作业4】下列说法中，正确的是（）

A．经过一点，有且只有一条直线与已知直线平行

B．两条直线被第三条直线所截同位角相等

C．同一平面内，垂直于同一条直线的两条直线互相垂直

D．两条直线被第三条直线所截，内错角相等，则两条直线平行

过直线外一点，有且只有一条直线与已知直线平行；

B错误：

同位角不一定相等；

C错误：

同一平面内，垂直于同一条直线的两条直线互相平行；

D.正确

【总结】