版高考数学一轮复习第3章三角函数解三角形33三角函数的图象与性质学案文.docx

版高考数学一轮复习第3章三角函数解三角形33三角函数的图象与性质学案文.docx

《版高考数学一轮复习第3章三角函数解三角形33三角函数的图象与性质学案文.docx》由会员分享，可在线阅读，更多相关《版高考数学一轮复习第3章三角函数解三角形33三角函数的图象与性质学案文.docx（21页珍藏版）》请在冰豆网上搜索。

版高考数学一轮复习第3章三角函数解三角形33三角函数的图象与性质学案文

3．3　三角函数的图象与性质

[知识梳理]

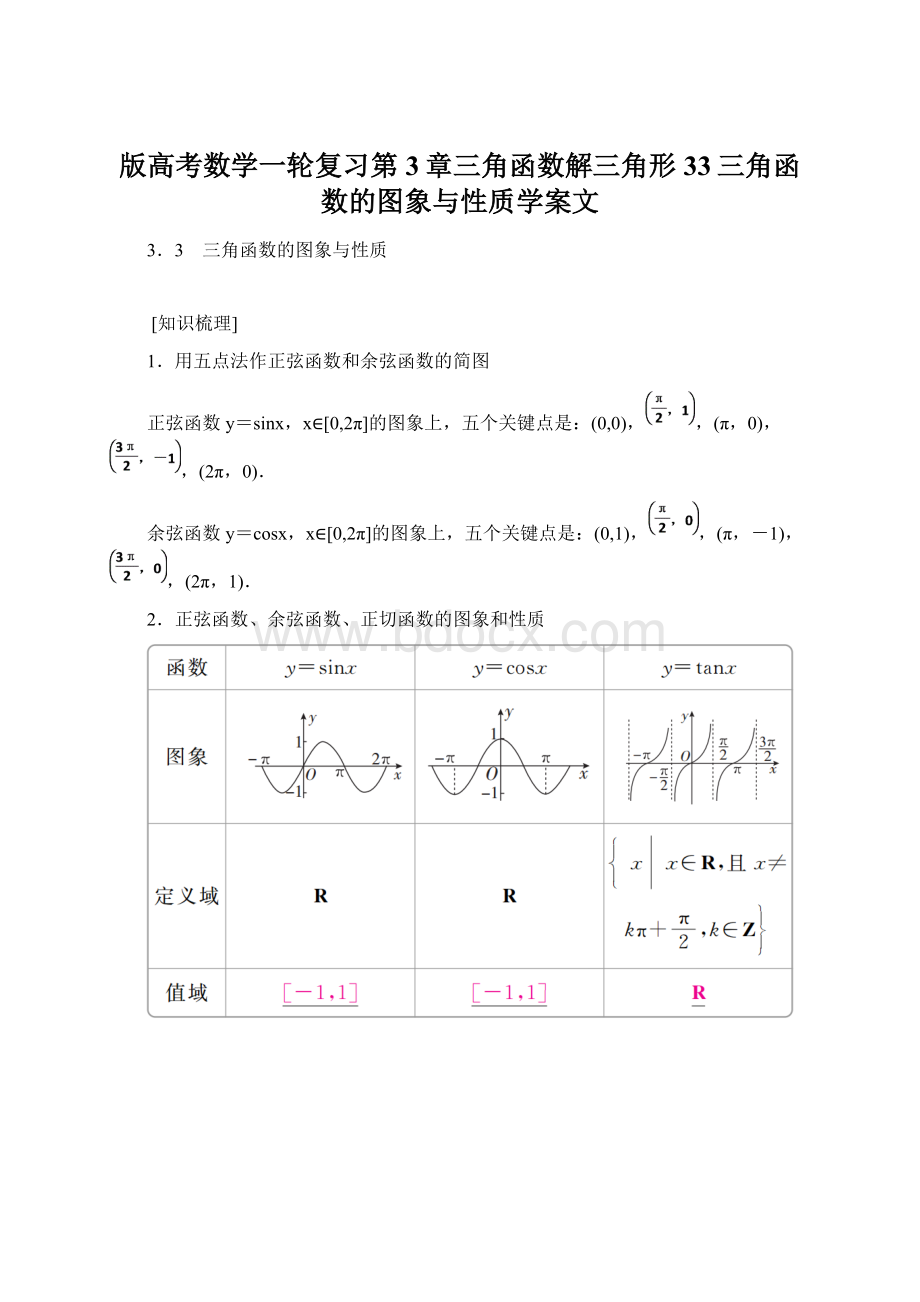
1．用五点法作正弦函数和余弦函数的简图

正弦函数y＝sinx，x∈[0,2π]的图象上，五个关键点是：

（0,0），，（π，0），，（2π，0）．

余弦函数y＝cosx，x∈[0,2π]的图象上，五个关键点是：

（0,1），，（π，－1），，（2π，1）．

2．正弦函数、余弦函数、正切函数的图象和性质

[诊断自测]

1．概念思辨

（1）y＝tanx在整个定义域上是增函数．（　　）

（2）函数f（x）＝sin（－2x）与f（x）＝sin2x的单调增区间都是（k∈Z）．（　　）

（3）由sin＝sin知，是正弦函数y＝sinx（x∈R）的一个周期．（　　）

（4）若非零实数T是函数f（x）的周期，则kT（k是非零整数）也是函数f（x）的周期．（　　）

答案　

（1）×　

（2）×　（3）×　（4）√

2．教材衍化

（1）（必修A4P46T2）函数f（x）＝（1＋tanx）cosx的最小正周期、最大值为（　　）

A．2π，2B.，C．π，2D.，

答案　A

解析　f（x）＝（1＋tanx）cosx＝·cosx＝2cos，则T＝2π.最大值为2.故选A.

（2）（必修A4P40T4）已知函数f（x）＝sin（x∈R），下列结论错误的是（　　）

A．函数f（x）是偶函数

B．函数f（x）的最小正周期为π

C．函数f（x）在区间上是增函数

D．函数f（x）的图象关于直线x＝对称

答案　D

解析　f（x）＝sin＝－cos2x，此函数为最小正周期为π的偶函数，所以A，B正确．由函数y＝cosx的单调性知C正确．函数图象的对称轴方程为x＝（k∈Z），显然，无论k取任何整数，x≠，所以D错误．故选D.

3．小题热身

（1）函数f（x）＝sin在区间上的最小值为（　　）

A．－1B．－C.D．0

答案　B

解析　由已知x∈，得2x－∈，所以sin∈，故函数f（x）＝sin在区间上的最小值为－.故选B.

（2）函数y＝tan的单调递增区间是________，最小正周期是________．

答案　（k∈Z）　2π

解析　由kπ－<＋

题型1　三角函数的定义域和值域　　　　　　　　　　　　　　　　　　　

函数f（x）＝＋log2（2sinx－1）的定义域是________．

本题采用数形结合．

答案　∪∪

解析　由题意，得

由①得－8≤x≤8，由②得sinx>，由正弦曲线得＋2kπ

所以不等式组的解集为∪∪.

　是否存在实数a，使得函数y＝sin2x＋acosx＋a－在

闭区间上的最大值是1？

若存在，求出对应的a值；若不存在，试说明理由．

用转化法将问题化为二次函数型，然后分类讨论．

解　y＝1－cos2x＋acosx＋a－＝－2＋＋a－.

当0≤x≤时，0≤cosx≤1.

若>1，即a>2，则当cosx＝1时，ymax＝a＋a－＝1⇒a＝<2（舍去），

若0≤≤1，即0≤a≤2，则当cosx＝时，ymax＝＋a－＝1⇒a＝或a＝－4<0（舍去）．

若<0，即a<0，则当cosx＝0时，ymax＝a－＝1⇒a＝>0（舍去）

综合上述，存在a＝符合题设．

方法技巧

1．三角函数定义域的求法

求三角函数定义域实际上是构造简单的三角不等式（组），常借助三角函数线或三角函数图象来求解．见典例1.

2．三角函数值域的不同求法

（1）形如y＝asinx＋bcosx＋k的三角函数化为y＝Asin（ωx＋φ）＋k的形式，再求值域（最值）．

（2）形如y＝asin2x＋bsinx＋k的三角函数，可先设sinx＝t，化为关于t的二次函数求值域（最值）．见典例2.

（3）形如y＝asinxcosx＋b（sinx±cosx）＋c的三角函数，可先设t＝sinx±cosx，化为关于t的二次函数求值域（最值）．

冲关针对训练

1．（2017·郑州模拟）已知函数f（x）＝sin，其中x∈，若f（x）的值域是，则实数a的取值范围是________．

答案　

解析　由x∈，知x＋∈.

∵x＋∈时，f（x）的值域为，

∴由函数的图象知≤a＋≤，所以≤a≤π.

2．已知3sin2α＋2sin2β＝2sinα，求y＝sin2α＋sin2β的取值范围．

解　∵3sin2α＋2sin2β＝2sinα，

∴sin2β＝－sin2α＋sinα，

∵0≤sin2β≤1，∴

解得0≤sinα≤，

∵y＝sin2α＋sin2β＝－sin2α＋sinα＝－（sinα－1）2＋，

0≤sinα≤，∴sinα＝0时，ymin＝0；sinα＝时，ymax＝，

∴0≤sin2α＋sin2β≤.

题型2　三角函数的单调性

（2017·长沙一模）函数y＝sin，x∈[－2π，2π]的单调递增区间是（　　）

A.B.

C.D.和

本题用子集法．

答案　D

解析　依题意得y＝－sin，当2kπ＋≤x－≤2kπ＋（k∈Z），即4kπ＋≤x≤4kπ＋（k∈Z）时，函数y＝－sin是单调递增函数．又x∈[－2π，2π]，因此函数y＝－sin，x∈[－2π，2π]的单调递增区间是和.选D.

　　已知ω>0，函数f（x）＝sin在上单调递减，则实数ω的取值范围是（　　）

A.B.C.D．（0,2]

子集反推法．

答案　A

解析　由

又y＝sinα在上递减，

所以解得≤ω≤.故选A.

方法技巧

1．求三角函数单调区间的方法

（1）代换法：

就是将比较复杂的三角函数含自变量的代数式整体当作一个角u（或t），利用复合函数的单调性列不等式求解．

（2）图象法：

画出三角函数的正、余弦曲线，结合图象求它的单调区间．

（3）子集法：

求出原函数的相应单调区间，由已知区间是所求某区间的子集，列不等式（组）求解．见典例1.

2．已知三角函数的单调区间求参数的取值范围的方法

（1）反子集法：

由所给区间求出整体角的范围，由该范围是某相应正、余弦函数的某个单调区间的子集，列不等式（组）求解．见典例2.

（2）周期法：

由所给区间的两个端点到其相应对称中心的距离不超过周期列不等式（组）求解．

提醒：

要注意求函数y＝Asin（ωx＋φ）的单调区间时ω的符号，若ω<0，那么一定先借助诱导公式将ω化为正数．同时切莫漏掉考虑函数自身的定义域．

冲关针对训练

1．（2017·济宁检测）下列函数中，周期为π，且在上为减函数的是（　　）

A．y＝sinB．y＝cos

C．y＝sinD．y＝cos

答案　A

解析　对于选项A，注意到y＝sin＝cos2x的周期为π，且在上是减函数．故选A.

2．（2017·莆田一模）已知函数f（x）＝sin（ωx＋

φ），A为f（x）图象的对称中心，B，C是该图象上相邻的最高点和最低点，若BC＝4，则f（x）的单调递增区间是（　　）

A.，k∈Z

B.，k∈Z

C.，k∈Z

D.，k∈Z

答案　C

解析　函数f（x）＝sin（ωx＋φ），A为f（x）图象的对称中心，B，C是该图象上相邻的最高点和最低点，∵BC＝4，

∴

（2）2＋2＝42，即12＋＝16，求得ω＝.

再根据·＋φ＝kπ，k∈Z，可得φ＝－，∴f（x）＝sin.

令2kπ－≤x－≤2kπ＋，求得4k－≤x≤4k＋，

故f（x）的单调递增区间为，k∈Z.

故选C.

题型3　三角函数的奇偶性及对称性

（2018·江西模拟）已知函数f（x）＝Acos（ωx＋φ）（A>0，

ω>0,0<φ<π）为奇函数，该函数的部分图象如图所示，△EFG是边长为2的等边三角形，则f

（1）的值为（　　）

A．－B．－C.D．－

数形结合思想．

答案　D

解析　∵f（x）＝Acos（ωx＋φ）为奇函数，

∴f（0）＝Acosφ＝0

∵0<φ<π，∴φ＝，

∴f（x）＝Acos＝－Asinωx.

∵△EFG是边长为2的等边三角形，则yE＝＝A，

又∵函数的周期T＝2FG＝4，根据周期公式可得，ω＝＝.

∴f（x）＝－Asinx＝－sinx，

则f

（1）＝－.故选D.

　　（2018·江南十校联考）已知函数f（x）＝sin（ωx＋

φ）的最小正周期为4π，且对∀x∈R，有f（x）≤f恒成立，则f（x）图象的一个对称中心是（　　）

A.B.

C.D.

应用公式法．

答案　A

解析　由f（x）＝sin（ωx＋φ）的最小正周期为4π，得ω＝.因为f（x）≤f恒成立，所以f（x）max＝f，即×＋φ＝＋2kπ（k∈Z）．由|φ|<，得φ＝，故f（x）＝sin.

令x＋＝kπ（k∈Z），得x＝2kπ－（k∈Z），

故f（x）图象的对称中心为（k∈Z）．当k＝0时，f（x）图象的对称中心为.故选A.

方法技巧

1．若f（x）＝Asin（ωx＋φ）为偶函数，则φ＝kπ＋（k∈Z），同时当x＝0时，f（x）取得最大或最小值．若f（x）＝Asin（ωx＋φ）为奇函数，则φ＝kπ（k∈Z），同时当x＝0时，f（x）＝0.见典例1.

2．解决对称性问题的关键：

熟练掌握三角函数的对称轴、对称中心．对于函数y＝Asin（ωx＋φ），其对称轴一定经过图象的最高点或最低点，对称中心的横坐标一定是函数的零点，因此在判断直线x＝x0或点（x0,0）是否是函数的对称轴或对称中心时，可通过检验f（x0）的值进行判断．见典例2.

冲关针对训练

1．（2017·揭阳模拟）当x＝时，函数f（x）＝sin（x＋φ）取得最小值，则函数y＝f（　　）

A．是奇函数且图象关于点对称

B．是偶函数且图象关于点（π，0）对称

C．是奇函数且图象关于直线x＝对称

D．是偶函数且图象关于直线x＝π对称

答案　C

解析　∵当x＝时，函数f（x）取得最小值，

∴sin＝－1，∴φ＝2kπ－（k∈Z），

∴f（x）＝sin＝sin，

∴y＝f＝sin（－x）＝－sinx，

∴y＝f是奇函数，且图象关于直线x＝对称．故选C.

2．（2018·南阳期末）已知函数f（x）＝，试讨论该函数的奇偶性、周期性以及在区间[0，π]上的单调性．

解　因为y＝＝＝|sinx|

＝所以作函数的图象如下：

所以，该函数是偶函数，周期为π.

在区间上是增函数，在区间上是减函数，在区间[0，π]上不是单调函数．

1．（2017·全国卷Ⅲ）设函数f（x）＝cos，则下列结论错误的是（　　）

A．f（x）的一个周期为－2π

B．y＝f（x）的图象关于直线x＝对称

C．f（x＋π）的一个零点为x＝

D．f（x）在单调递减

答案　D

解析　因为f（x）＝cos的周期为2kπ（k∈Z），所以f（x）的一个周期为－2π，A项正确．因为f（x）＝cos图象的对称轴为直线x＝kπ－（k∈Z），所以y＝f（x）的图象关于直线x＝对称，B项正确．f（x＋π）＝cos.令x＋＝kπ＋（k∈Z），得x＝kπ－π，当k＝1时，x＝，所以f（x＋π）的一个零点为x＝，C项正确．因为f（x）＝cos的递减区间为（k∈Z），递增区间为（k∈Z），所以是减区间，是增区间，D项错误．故选D.

2．（2018·舟山模拟）若函数f（x）＝3sin（2x＋θ）（0<θ<π）是偶函数，则f（x）在[0，π]上的递增区间是（　　）

A.B.C.D.

答案　B

解析　∵函数f（x）＝3sin（2x＋θ）（0<θ<π）是偶函数，∴θ＝，f（x）＝3sin＝3cos2x，令2kπ－π≤2x≤2kπ，求得kπ－≤x≤kπ，可得函数f（x）的增区间为（k∈