007第七章凸轮Word格式.docx

007第七章凸轮Word格式.docx

《007第七章凸轮Word格式.docx》由会员分享，可在线阅读，更多相关《007第七章凸轮Word格式.docx（25页珍藏版）》请在冰豆网上搜索。

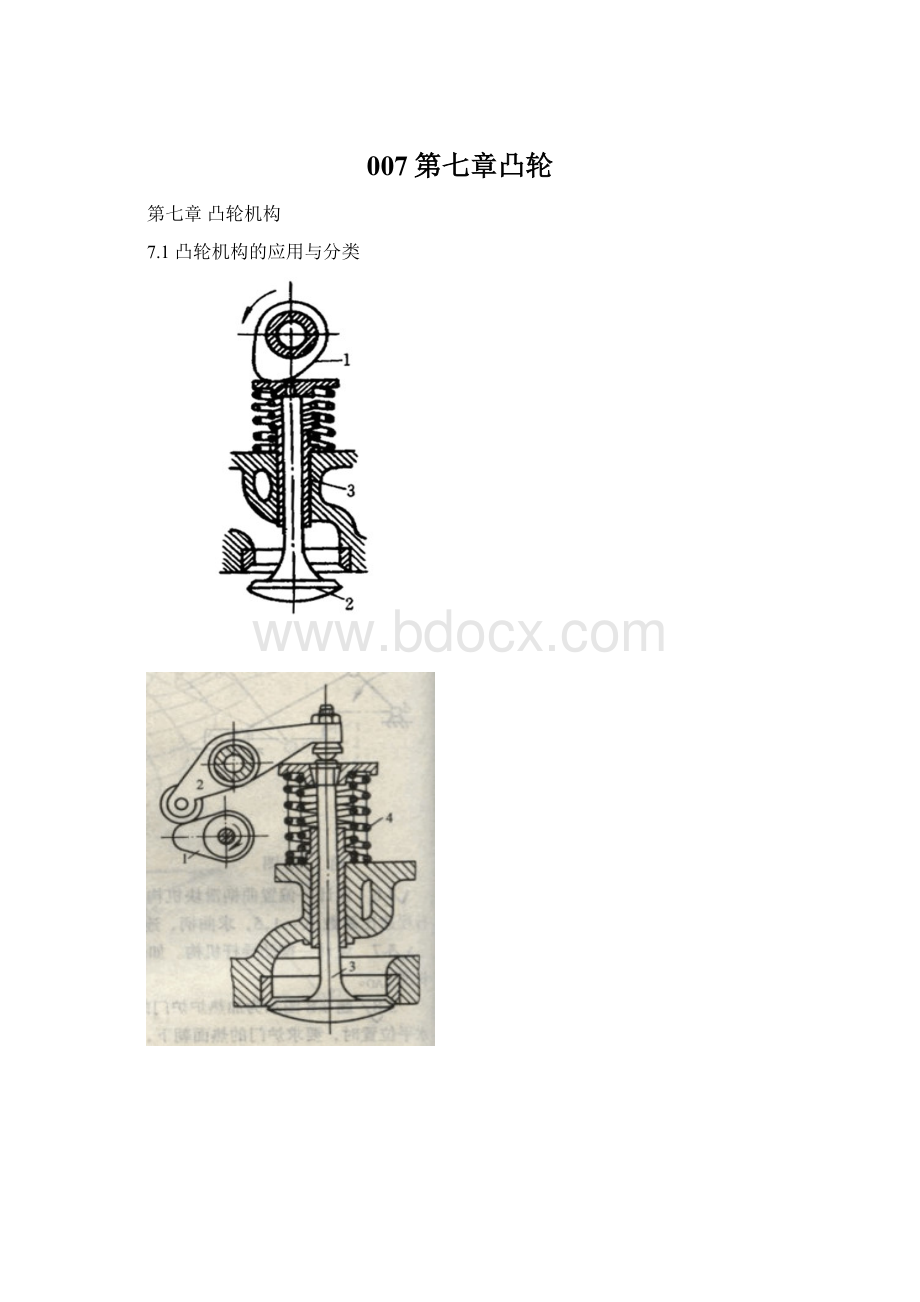
凸轮的轮廓线→从动件的运动规律。

结构简单，紧凑，工作可靠。

易磨损，工作速度不高。

2凸轮机构的类型：

1）按凸轮的形状分

盘形凸轮,移动凸轮,圆柱凸轮

图7-3（a）所示为盘形凸轮，是一个具有变化向径的盘形构件。

当它绕固定轴转动时，可推动从动件在垂直于凸轮轴的平面内运动。

图7-3（b）所示为移动凸轮，可看作是回转中心在无穷远处的盘形凸轮。

当移动凸轮作直线往复运动时，可推动从动件在同一运动平面内运动。

图7-3（c）所示为圆柱凸轮，这种凸轮是一个在圆柱面上开有曲线凹槽，或是在圆柱面上作出曲线轮廓的构件。

当它转动时，可使从动件在平行于其轴线或包括其轴线的平面内运动。

由于凸轮与从动件的运动不在同一平面内，所以这是一种空间凸轮机构。

2）按从动件类型分：

尖顶从动件,滚子从动件,平底从动件

如图7-4（a）、（b）所示为尖顶（端）从动件。

尖端能与任意复杂的凸轮轮廓保持接触，从而使从动件实现任意运动，适用于传力不大的低速凸轮机构中。

如图7-4（c）、（d）所示为滚子从动件，这种从动件由于滚子与凸轮之间为滚动摩擦，磨损较小，故可用来传递较大的力。

如图7-4（e）、（f）所示为平底从动件，这种从动件的优点是不计摩擦时凸轮对从动件的作用力始终垂直于从动件的底边，受力比较平稳。

而且凸轮与平底的接触面容易形成楔形油膜，常用于高速凸轮机构中。

3）按凸轮与从动件保持接触的方式分：

力锁合,几何锁合：

图7-5（b）、（c）所示凸轮机构中，其从动件上分别装有相对位置不变的两个底或两个滚子，凸轮运动时，其轮廓能保证始终与两个平底或滚子同时接触。

图（b）所示常称为等宽凸轮，图（c）所示常称为等径凸轮。

图7-5（d）所示为一共轭凸轮（又称主回凸轮）机构。

7.2从动件的运动规律

7.2.1描述凸轮机构的参数

图7-6（a）所示为一尖端从动件盘形凸轮机构。

对于凸轮，以凸轮轮廓最小的向径r0为半径所作的圆称为凸轮的基圆。

A为动件开始上升的位置，凸轮逆时针转动，轮廓曲线AB与尖端作用将从动件推向远方，待B转到B＇时，从动件上升到距凸轮回转中心最远的位置，凸轮所转过角度,称为推程运动角；

在BC弧段，从动件在最远位置停留，所对应的凸轮转角称为远休止角；

在CD弧段，从动件以一定规律返回至初始位置，这时凸轮所转过的角度称为回程运动角；

当圆弧DA与尖端作用时，从动件在距凸轮回转中心最近位置停留，所对应的凸轮转角称为近休止角。

图（b）是描述从动件位移与凸轮转角之间对应关系的从动件位移线图。

参数：

1．基圆：

2．升程、升程运动角：

3．回程、回程运动角：

4．远休止角、近休止角

5．位移线图

7.2.2从动件的常用运动规律

1．等速运动规律

加速度在理论上突变为无穷大，由于材料的弹性，也会引起非常大的惯性力，在机构中引起刚性冲击。

需修正后才能使用，适用于低速的场合。

等速运动的修正：

图7-11所示为等加速---等速---等减速组合运动规律线图。

这种规律的加速度线图是不连续的，还存在柔性冲击

2．等加速等减速运动：

加速度曲线是水平直线，

速度曲线是斜直线，

位移曲线是两段在行程中点处光滑相连的抛物线。

由于在运动的起点、中点和终点处，加速度出现了有限值的突变，会引起惯性力的相应变化，在机构中引起柔性冲击。

适用于中速的场合

3．余弦加速度运动（简谐运动规律）：

图7-9为余弦加速度运动规律的运动线图。

速度线图为正弦曲线。

位移线图按简谐运动规律，余弦加速度运动又称为简谐运动规律。

加速度线图在全程范围内光滑连续，但在始、末两处具有突变，故对停---升---停型运动，引起柔性冲击，只适用于中速。

但对升---降---升型运动来说，远、近休止角均为零，加速度曲线为连续曲线，无冲击存在，这时可应用于高速。

4．正弦加速度运动：

（摆线运动规律）

位移线图按摆线运动规律，正弦加速度运动又称为摆线运动规律。

速度线图为余弦函数。

加速度线图为正弦曲线，在全程范围内光滑连续，没有突变，故不会引起柔性冲击，只适用于高速。

7.3用图解法设计凸轮的轮廓曲线

反转法原理：

1.偏置的直动从动件盘形凸轮机构 

1）偏置的直动尖顶从动件盘形凸轮机构

2）偏置的直动滚子从动件盘形凸轮机构 

3）直动平底从动件盘形凸轮机构 

2.摆动从动件盘形凸轮机构：

7.4用解析法设计凸轮的轮廓曲线

1．偏置直动滚子从动件盘形凸轮机构：

1）理论轮廓方程。

滚子转动中心的方程

x=（s0+s）sinδ+ecosδ

y=（s0+s）cosδ-esinδ

2）实际廓线方程。

滚子切点的方程

tanθ=（dx/dδ）/（-dy/dδ）

x’=x-rrcosθ

y’=y-rrsinθ

3）刀具中心轨迹方程：

刀具中心的方程

2．摆动滚子从动件盘形凸轮机构

3．直动平底从动件盘形凸轮机构：

7.5凸轮机构的基本尺寸

1）凸轮机构的作用力与凸轮机构的压力角

图7-20所示为一尖端直动推杆盘形凸轮机构在推和中任一位置的受力情况。

为从动件上作用的载荷，包括工作阻力、重力、弹簧力和惯性力，为凸轮作用于从动件的驱动力，

、

分别为导轨两侧作用于从动件上的总反力，

、

为摩擦角。

2）凸轮基圆半径的确定

3）滚子半径的选择 

4）平底长度的确定