一元一次方程应用难题精选含答案解析Word下载.docx

一元一次方程应用难题精选含答案解析Word下载.docx

《一元一次方程应用难题精选含答案解析Word下载.docx》由会员分享，可在线阅读，更多相关《一元一次方程应用难题精选含答案解析Word下载.docx（24页珍藏版）》请在冰豆网上搜索。

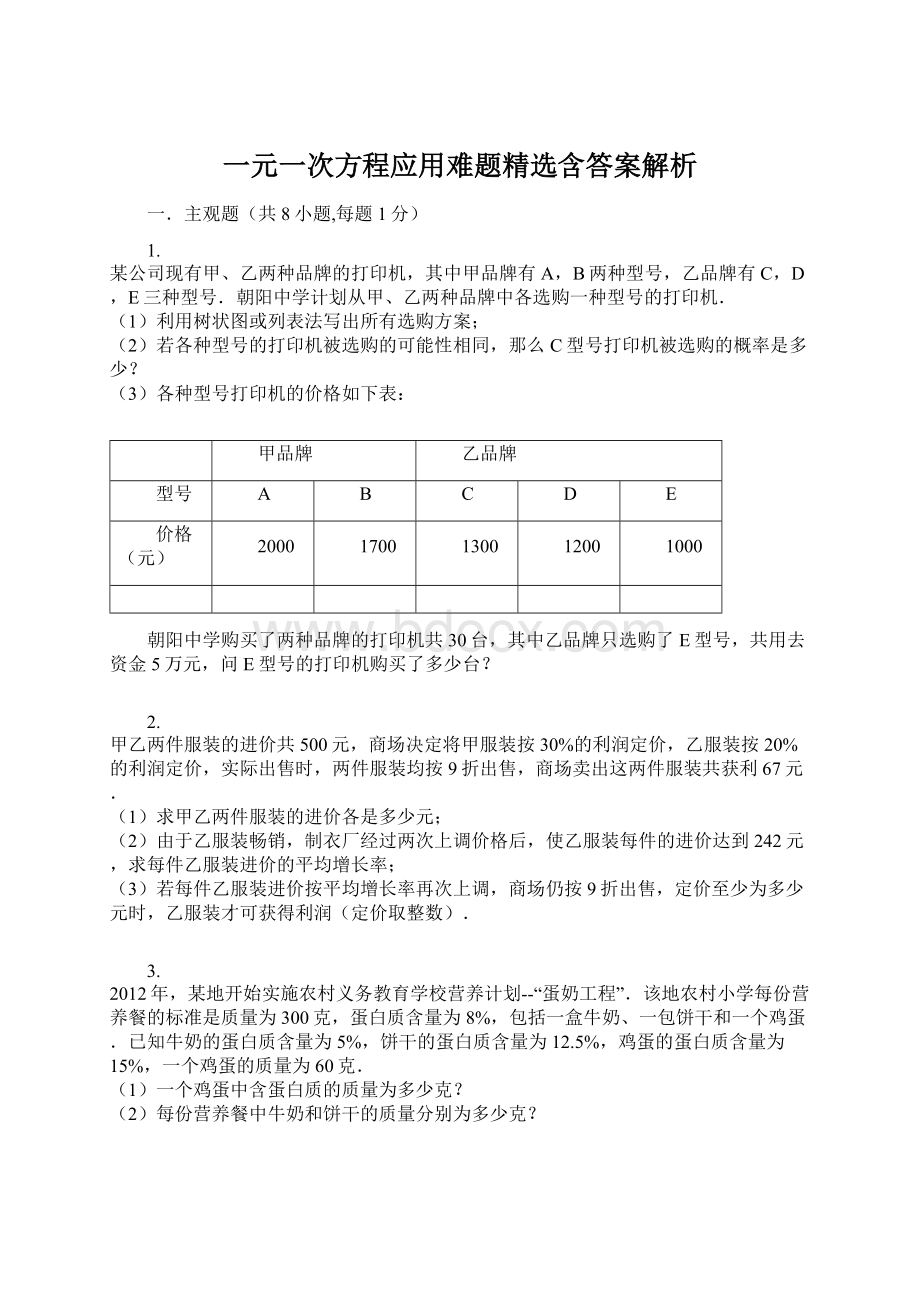
（1）该店购进A，B两种香油各多少瓶？

（2）将购进140瓶香油全部销售完可获利多少元？

（3）老板打算再以原来的进价购进A，B两种香油共200瓶，计划投资不超过1 

420元，且按原来的售价将这200瓶香油销售完成获利不低于339元，请问有哪几种购货方案？

5.

某校科技夏令营的学生在3位老师的带领下，准备赴北京大学参观，体验大学生活．现有两家旅行社前来洽谈，报价均为每人2000元，且各有优惠．希望旅行社表示：

带队老师免费，学生按8折收费；

青春旅行社表示师生一律按7折收费，经核算发现，参加两家旅行社的实际费用正好相等

（1）该校参加科技夏令营的学生共有多少人？

（2）如果又增加了部分学生，学校应选择哪家旅行社？

为什么？

6.

7.

一项工程，甲，乙两公司合作，12天可以完成，共需付施工费102000元；

如果甲，乙两公司单独完成此项工程，乙公司所用时间是甲公司的1.5倍，乙公司每天的施工费比甲公司每天的施工费少1500元．

（1）甲，乙两公司单独完成此项工程，各需多少天？

（2）若让一个公司单独完成这项工程，哪个公司的施工费较少？

8.

义洁中学计划从荣威公司购买A、B两种型号的小黑板，经洽谈，购买一块A型小黑板比买一块B型小黑板多用20元．且购买5块A型小黑板和4块B型小黑板共需820元．

（1）求购买一块A型小黑板、一块B型小黑板各需要多少元？

（2）根据义洁中学实际情况，需从荣威公司购买A、B两种型号的小黑板共60块，要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的

．请你通过计算，求出义洁中学从荣威公司购买A、B两种型号的小黑板有哪几种方案？

二．填空题（共15小题,每题0分）

甲、乙两人从A点同时同向出发沿400米的环形跑道跑步，过一段时间后，甲在跑道上离A点200米处，而乙在离A点不到100米处正向A点跑去．若甲、乙两人的速度比是4：

3，则此时乙至少跑了___________米．

电子跳蚤落在数轴上的某点k，第一步从k向左跳1个单位到k1，第二步由k1向右跳2个单位到k2，第三步由k向左跳3个单位到k3，第四步由k3向右跳4个单位到k4，…，按以上规律跳了100步时，电子跳蚤落在数轴上的点k100所表示的数恰是19.94．则电子跳蚤的初始位置k点所表示的数是___________．

第三届中国大学生方程式汽车比赛赛前，甲、乙两辆参赛小汽车在一个封闭的环形跑道内进行耐久测试．两车从同一地点沿相同方向同时起步后，乙车速超过甲车速，在第15分钟时甲车提速，在第18分钟时甲车追上乙车并且开始超过乙，在第23分钟时，甲车再次追上乙车．已知在测试中甲、乙两车均是匀速行驶，那么如果甲车不提速，乙车首次超过甲车所用的时间是___________分钟．

去年暑假某同学为锻炼自己，通过了解市场行情，从批发市场购进若干件印有“设计未来”标志的文化衫到自由市场去销售．首先按批发价提高25%销售了进货的60%，若要使最终赢利35%，则应在现行售价的基础上提高___________%销售完剩余的文化衫．

某电脑公司在5月1日将500台电脑投放市场，经市场调研发现，该批电脑每隔10天平均日销售量减少2台，现准备用38天销售完该批电脑，则预计该公司5月1日至5月10日的平均日销售量是___________台．

某人在同一条路上来回一次共用2小时．来时步行，平均速度是5千米/小时；

回去的时坐公共汽车，平均速度是20千米/小时，则这条路长是___________千米．

某市居民用电价格改革方案已出台，为鼓励居民节约用电，对居民生活用电实行阶梯制价格（见表）：

“一户一表”用电量

不超过a千瓦时

超过a千瓦时的部分

单价（元/千瓦时）

0.5

0.6

小芳家二月份用电200千瓦时，交电费105元，则a=___________．

某地按以下规定收取每月电费：

用电量如果不超过60度，按每度电0.8元收费；

如果超过60度则超过部分按1.2元收费．已知某用户3月份交电费66元．那么3月份该用户用电量为___________度．

9.

已知AB是一段只有3米长的窄道路，由于一辆小汽车与一辆大卡车在AB段相遇，必须倒车才能继续通过．如果小汽车在AB段正常行驶需10分钟，大卡车在AB段正常行驶需20分钟，小汽车在AB段倒车的速度是它正常行驶速度的

，大卡车在AB段倒车的速度是它正常行驶的

，小汽车需倒车的路程是大卡车的4倍．问两车都通过AB这段狭窄路面的最短时间是___________分钟．

10.

11.

一杯“可乐”饮料售价3.6元，商家为了促销，顾客每买一杯“可乐”饮料获一张赠券，每三张赠券可兑换一杯“可乐”饮料，则每张赠券的价值相当于___________元．

12.

某公司生产的一种饮料由A、B两种原液按一定比例配制而成，其中A原液成本价为10元/千克，B原液为15元/千克，按现行价格销售每千克获得60%的利润率．由于物价上涨，A原液上涨20%，B原液上涨10%，配制后的总成本增加15%，公司为了拓展市场，打算再投入现行总成本的25%做广告宣传，使得销售成本再次增加，如果要保证每千克的利润率不变，则此时这种饮料的售价与原售价之差为___________元/千克．

13.

“家电下乡”农民得实惠．村民小郑购买一台双门冰箱，在扣除13%的政府财政补贴后，再减去商场赠送的“家电下乡”消费券100元，实际只花了1988元钱，那么他购买这台冰箱节省了___________元钱．

14.

有一群麻雀，其中一部分在树上欢歌，另一部分在地上觅食，树上的一只麻雀对地上觅食的麻雀说：

“若从你们中飞上来一只，则树下的麻雀就是这群麻雀总数的

；

若从树上飞下去一只，则树上、树下的麻雀就一样多了．”那么这群麻雀一共有___________只．

15.

小明同学买了一包弹球，其中

是绿色的，

是黄色的，余下的

是蓝色的．如果有12个蓝色的弹球，那么，他总共买了___________个弹球．

三．单选题（共6小题,每题0分）

某商家售出两种商品皆为120元，其中一种商品盈利25%另一种商品亏损25%，则商家在这次交易中的盈亏情况为（）

A．盈

B．亏

C．不盈不亏

D．不清楚

一件服装标价200元，若以6折销售，仍可获利20%，则这件服装的进价是（）

A．100元

B．105元

C．108元

D．118元

小明从家里骑自行车到学校，每小时骑15km，可早到10分钟，每小时骑12km就会迟到5分钟．问他家到学校的路程是多少km？

设他家到学校的路程是xkm，则据题意列出的方程是（）

A．

B．

C．

D．

某道路一侧原有路灯106盏，相邻两盏灯的距离为36米，现计划全部更换为新型的节能灯，且相邻两盏灯的距离变为70米，则需更换的新型节能灯有（）

A．54盏

B．55盏

C．56盏

D．57盏

某商场对顾客实行优惠，规定：

（1）如一次购物不超过200元，则不予折扣；

（2）如一次购物超过200元但不超过500元的，按标价给予九折优惠；

（3）如一次购物超过500元的，其中500元按第

（2）条给予优惠，超过500元的部分则给予八折优惠．

某人两次去购物，分别付款168元与423元，如果他只去一次购买同样的商品，则应付款是（）

A．522.8元

B．510.4元

C．560.4元

D．472.8元

2010年“地球停电一小时”活动的某地区烛光晚餐中，设座位有x排，每排坐30人，则有8人无座位；

每排坐31人，则空26个座位．则下列方程正确的是（）

A．30x-8=31x+26

B．30x+8=31x+26

C．30x-8=31x-26

D．30x+8=31x-26

---------答题卡---------

一．主观题

1.答案：

E型号的打印机应选购10台．

1.解释：

分析：

依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率；

根据资金得到相应的方程，求解即可．

解答：

解：

（1）所列树状图或列表表示为：

D

E 

A，C 

A，D 

A，E 

B，C 

B，D 

B，E 

结果为：

（A，C），（A，D），（A，E），（B，C），（B，D），（B，E）；

（2）由

（1）知C型号的打印机被选购的概率为

（3）设选购E型号的打印机x台（x为正整数），则选购甲品牌（A或B型号）（30-x）台，由题意得：

当甲品牌选A型号时：

1000x+（30-x）×

2000=50000，解得x=10，

当甲品牌选B型号时：

1700=50000，解得

（不合题意），

故E型号的打印机应选购10台．

点评：

本题着重考查了用树状图列举随机事件出现的所有情况，并求出某些事件的概率，但应注意在求概率时各种情况出现的可能性务必相同．用到的知识点为：

概率=所求情况数与总情况数之比．

2.答案：

定价至少为296元时，乙服装才可获得利润．

2.解释：

（1）若设甲服装的进价为x元，则乙服装的进价为（500-x）元．根据公式：

总利润=总售价-总进价，即可列出方程．

（2）利用乙服装的进价为200元，经过两次上调价格后，使乙服装每件的进价达到242元，利用增长率公式求出即可；

（3）利用每件乙服装进价按平均增长率再次上调，再次上调价格为：

242×

（1+10%）=266.2（元），进而利用不等式求出即可．

（1）设甲服装的进价为x元，则乙服装的进价为（500-x）元，

根据题意得：

90%•（1+30%）x+90%•（1+20%）（500-x）-500=67，

解得：

x=300，

500-x=200．

答：

甲服装的进价为300元、乙服装的进价为200元．

（2）∵乙服装的进价为200元，经过两次上调价格后，使乙服装每件的进价达到242元，

∴设每件乙服装进价的平均增长率为y，

则200（1+y）2=242，

y1=0.1=10%，y2=-2.1（不合题意舍去）．

每件乙服装进价的平均增长率为10%；

（3）∵每件乙服装进价按平均增长率再次上调，

∴再次上调价格为：

（1+10%）=266.2（元），

∵商场仍按9折出售，设定价为a元时，

0.9a-266.2＞0，

a＞

．

故定价至少为296元时，乙服装才可获得利润．

此题主要考查了一元二次方程的应用以及增长率问题和一元一次不等式的应用，注意售价的算法：

售价=定价×

打折数．

3.答案：

饼干的质量为：

300-60-x=40．

每份营养餐中牛奶和饼干的质量分别为200克和40克．

3.解释：

（1）鸡蛋中蛋白质的质量=鸡蛋的重量×

鸡蛋的蛋白质含量就可以直接求出答案；

（2）设每份营养餐中牛奶的质量为x克，则饼干的质量为（300-60-x）克，根据题意列出方程求出其解就可以

（1）由题意得：

60×

15%=9（克）．

一个鸡蛋中含蛋白质的质量为9克．

（2）设每份营养餐中牛奶的质量为x克，则饼干的质量为（300-60-x）克，由题意得：

5%x+12.5%（300-60-x）+60×

15%=300×

8%

x=200．

故饼干的质量为：

本题考查了列一元一次方程解实际问题的运用，根据各种食品的蛋白质的和加起来等于总蛋白质就可以建立方程，在解答时确定等量关系是关键．

4.答案：

方案1：

A种香油120瓶B种香油80瓶．

方案2：

A种香油121瓶B种香油79瓶．

方案3：

A种香油122瓶B种香油78瓶．

（1）该店购进A种香油80瓶，B种香油60瓶．

（2）将购进的140瓶全部销售完可获利240元．

（3）有三种购货方案：

方案1：

A种香油120瓶B种香油80瓶；

A种香油121瓶B种香油79瓶；

4.解释：

（1）求A，B两种香油各购进多少瓶，根据题意购进140瓶，共花了1 

000元，可列方程求解即可．

（2）在

（1）的基础之上已经得出A，B两种香油购进的瓶数，算出总价减去总进价即可得出获利多少．

（3）由题意可列不等式组，解得120≤a≤122．因为a为非负整数，所以a取120，121，122．所以200-a=80或79或78．

（1）设：

该店购进A种香油x瓶，B种香油（140-x）瓶，

由题意可得6.5x+8（140-x）=1000，

解得x=80，140-x=60．

该店购进A种香油80瓶，B种香油60瓶．

（2）80×

（8-6.5）+60×

（10-8）=240．

将购进140瓶香油全部销售完可获利240元．

（3）设：

购进A种香油a瓶，B种香油（200-a）瓶，

由题意可知6.5a+8（200-a）≤1420

1.5a+2（200-a）≥339

解得120≤a≤122．

因为a为非负整数，

所以a取120，121，122．

所以200-a=80或79或78．

故方案1：

本题考查一元一次不等式组的应用，读懂题列出不等式关系式即可求解．

5.答案：

如果又增加了部分学生，学校应选择青春旅行社合算．

5.解释：

（1）设该校参加科技夏令营的学生共有x人，根据题意可得等量关系：

在希望旅行社的花费为2000x×

8折=在青春旅行社的花费为2000（x+3）×

7折，根据等量关系列出方程解方程即可；

（2）设学生总数为a人，在希望旅行社的花费为2000a×

8折，在青春旅行社的花费为2000（a+3）×

7折，

如果选择希望旅行社合算，则2000a×

80%＜2000（a+3）×

70%，

如果选择青春旅行社合算，则2000a×

80%＞2000（a+3）×

解不等式即可知道如果又增加了部分学生，学校应选择哪家旅行社．

（1）设该校参加科技夏令营的学生共有x人，由题意得：

2000x×

80%=2000（x+3）×

x=21，

该校参加科技夏令营的学生共有21人；

（2）设学生总数为a人，由题意得：

a＜21，

a＞21，

故如果又增加了部分学生，学校应选择青春旅行社合算．

此题主要考查了一元一次方程与一元一次不等式的应用，关键是设出学生人数，表示出在希望旅行社的花费和在青春旅行社的花费．

6.答案：

6.解释：

7.答案：

甲公司单独完成此项工程，需20天，乙公司单独完成此项工程，需30天；

（2）设甲公司每天的施工费为y元，则乙公司每天的施工费为（y-1500）元，

根据题意得12（y+y-1500）=102000，解得y=5000，

甲公司单独完成此项工程所需的施工费：

20×

5000=100000（元）；

乙公司单独完成此项工程所需的施工费：

30×

（5000-1500）=105000（元）；

故甲公司的施工费较少．

7.解释：

（1）设甲公司单独完成此项工程需x天，则乙工程公司单独完成需1.5x天，根据合作12天完成列出方程求解即可．

（2）分别求得两个公司施工所需费用后比较即可得到结论．

（1）设甲公司单独完成此项工程需x天，则乙公司单独完成此项工程需1.5x天．

根据题意，得

+

=

，

解得x=20，

经检验知x=20是方程的解且符合题意．

1.5x=30

故甲公司单独完成此项工程，需20天，乙公司单独完成此项工程，需30天；

本题考查了分式方程的应用，解题的关键是从实际问题中整理出等量关系并利用等量关系求解．

8.答案：

8.解释：

（1）设购买一块A型小黑板需要x元，一块B型为（x-20）元，根据，购买一块A型小黑板比买一块B型小黑板多用20元．且购买5块A型小黑板和4块B型小黑板共需820元可列方程求解．

（2）设购买A型小黑板m块，则购买B型小黑板（60-m）块，根据需从荣威公司购买A、B两种型号的小黑板共60块，要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的

，可列不等式组求解．

（1）设购买一块A型小黑板需要x元，一块B型为（x-20）元，

5x+4（x-20）=820，

x=100，

x-20=80，

购买A型100元，B型80元；

（2）设购买A型小黑板m块，则购买B型小黑板（60-m）块，

∴20＜m≤22，

而m为整数，所以m为21或22．

当m=21时，60-m=39；

当m=22时，60-m=38．

所以有两种购买方案：

方案一购买A21块，B39块、

方案二购买A22块，B38块．

本题考查理解题意的能力，关键根据购买黑板块数不同钱数的不同求出购买黑板的钱数，然后要求购买A、B两种型号小黑板的总费用不超过5240元．并且购买A型小黑板的数量应大于购买A、B种型号小黑板总数量的

，列出不等式组求解．

二．填空题

750米．

因为甲、乙两人的速度比是4：

3，所以，甲、乙两人的路程比S甲：

S乙=4：

3；

由过一段时间后，甲在跑道上离A点200米处，所以，甲跑的路程为：

S甲=400k+200米（k为自然数），此时，乙在离A点不到100米处正向A点跑去；

再由题意分类讨论解答．

设甲、乙两人的路程分别为S甲、S乙，由题意知，S甲：

由过一段时间后，甲在跑道上离A点200米处，根据题意，得S甲=400k+200米（k为自然数），

①当k=0时，S乙=

×

（400×

0+200）=150米