第九章 配伍区组设计资料的统计分析的Stata实现Word文档下载推荐.docx

第九章 配伍区组设计资料的统计分析的Stata实现Word文档下载推荐.docx

《第九章 配伍区组设计资料的统计分析的Stata实现Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《第九章 配伍区组设计资料的统计分析的Stata实现Word文档下载推荐.docx（16页珍藏版）》请在冰豆网上搜索。

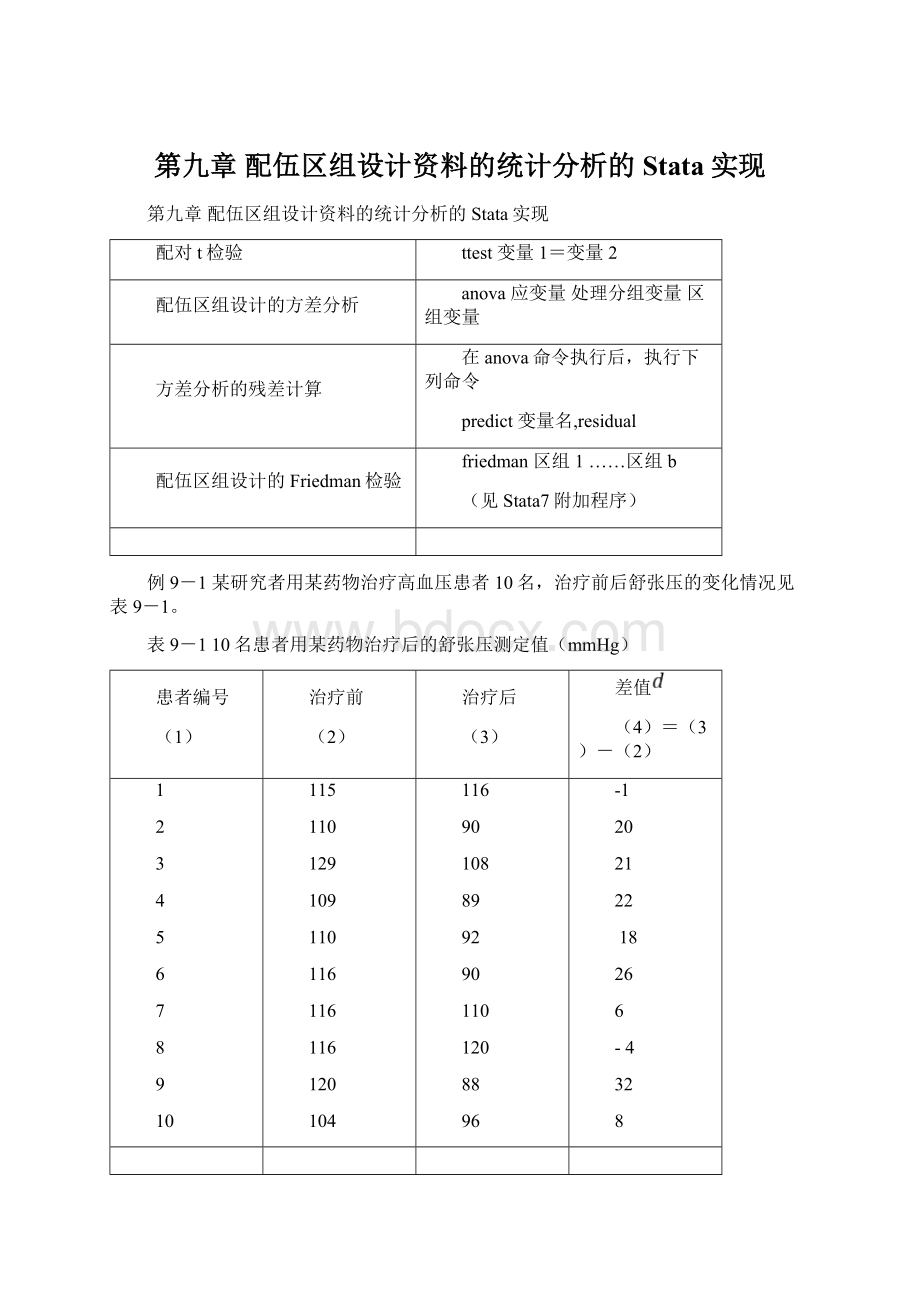
104

90

108

89

92

88

96

-1

20

21

22

18

26

-4

32

Stata数据为：

x1

x2

Stata命令为：

ttestx1=x2

结果为：

Pairedttest

------------------------------------------------------------------------------

Variable|ObsMeanStd.Err.Std.Dev.[95%Conf.Interval]

---------+--------------------------------------------------------------------

x1|10114.52.1819976.900081109.564119.436

x2|1099.93.89429812.3148591.09049108.7095

diff|1014.63.72737611.7876.16808923.03191

Ho:

mean（x1-x2）=mean（diff）=0

Ha:

mean（diff）<

0Ha:

mean（diff）!

=0Ha:

mean（diff）>

0

t=3.9170t=3.9170t=3.9170

P<

t=0.9982P>

|t|=0.0035P>

t=0.0018

P=0.0035，治疗前后舒张压有差别，治疗后下降。

例9－2某研究者对8名冻疮患者足部的两个冻疮部位（两个部位冻疮程度非常接近）用两种不同药物治疗，分别观测两个冻疮部位的痊愈时间，结果见表9－2。

表9－2两种方法测定患者冻疮痊愈时间时间（天）结果

受试者编号

药物1

药物2

12

11

1.建立检验假设，确定检验水准

，两种药物治疗的冻疮痊愈平均时间相同

，两种药物治疗的冻疮痊愈平均时间不同

x1|87.875.2.1671246.0632399.686761

x2|810.28.32795811.67204

diff|8-2.1251.0763283.044316-4.670111.

mean（diff）=mean（x1-x2）t=-1.9743

mean（diff）=0degreesoffreedom=7

Pr（T<

t）=0.0445Pr（|T|>

|t|）=0.0889Pr（T>

t）=0.9555

=1.9743，则P＝0.0889，在

水平上不拒绝

，差值的样本均数与已知总体均数的比较，差异无统计学意义，故尚不能认为该两种药物治疗的冻疮痊愈平均时间不同。

例9－3为了解不同治疗方法对高胆固醇血症的疗效，根据专业要求，在采取相关清洗或洗脱措施，保证相邻两次疗效不受影响的前提下，某研究者用3种不同方法对9只受试动物进行实验，其血浆胆固醇测定值（mmol/L）见表9－3。

表9－33种治疗方法的血浆胆固醇测定结果（mmol/L）

动物编号

甲方法

乙方法

丙方法

10.10

6.78

13.22

7.78

7.47

6.11

6.02

8.08

7.56

6.69

5.40

12.67

6.56

5.65

5.26

5.43

6.26

5.06

7.74

6.83

10.95

7.20

6.85

5.88

5.79

7.87

6.45

b

g

x

10.1

6.78

7.78

7.47

6.11

6.02

8.08

7.56

6.69

5.4

6.56

5.65

5.26

5.43

6.26

5.06

7.2

6.85

5.79

anovaxgb

Numberofobs=27R-squared=0.9378

RootMSE=.672582AdjR-squared=0.8988

Source|PartialSSdfMSFProb>

F

-----------+----------------------------------------------------

Model|109.0373281010.24.100.0000

|

g|11.25.12.300.0006

b|97.812.27.060.0000

Residual|7.16.

Total|116.275188264.

P=0.0006，3种不同方法得到的血浆胆固醇测定值（mmol/L）不全相同。

例9－4将30只小白鼠按体重、性别、窝别、活泼性分成10个区组，每个区组的3只小白鼠随机分配到3个实验组，分别以不同蛋白质饲料进行喂养，60天后测量小白鼠的体重增加量（g），数据如表9－4。

表9－4三种饲料喂养30只小白鼠的体重增加量（g）

区组

饲料

Ⅰ

Ⅱ

Ⅲ

30

40

41

36

48

33

45

37

44

62

52

49

55

53

77

68

76

81

84

78

75

73

74

72

针对处理组

H0：

三种不同饲料喂养的小白鼠体重平均增加量相同

H1：

三种不同饲料喂养的小白鼠体重平均增加量不同或不全相同

针对区组

H0：

对于任何一种饲料喂养，10个区组的小白鼠平均体重增加量相同

H1：

对于任何一种饲料喂养，10个区组的小白鼠平均体重增加量不同或不全相同

Numberofobs=30R-squared=0.9250

RootMSE=6.00339AdjR-squared=0.8791

Model|7997.1333311727.01212120.170.0000

g|7565.2666723782.63333104.950.0000

b|431.866667947.1.330.2884

Residual|648.7333331836.

Total|8645.8666729298.133333

则P处理<

0.01，P区组>

0.05，表9－6中P值为统计软件计算后直接给出的数值。

可以说明，对于处理效应，按

水准，拒绝H0，可认为三种不同饲料喂养的小白鼠平均体重增加量不同或不全相同或至少有两个总体均数不同；

对于区组，按

水准，不拒绝H0，还不能认为10个区组小白鼠的平均体重增加量不同或不全相同。

例9－6某研究者采用1：

1配对方法将16例肝炎患者分别分在两种不同治疗方法组，测定其血中GPT含量（iu/L），资料如表9－6第

（2）、（3）栏，问：

用不同方法治疗的患者GPT含量有无差别？

表9－6不同治疗方法的肝炎患者血中GPT含量（iu/L）

对子号

方法1

方法2

（4）＝

（2）－（3）

秩次

（5）

112

84

30

17

103

233

31

124

38

69

79

-45

203

-38

－

-3.5

-2

3.5

17

，差值的总体中位数为0

，差值的总体中位数不为0

signrankx1=x2

Wilcoxonsigned-ranktest

sign|obssumranksexpected

-------------+---------------------------------

positive|527.517.5

negative|27.517.5

zero|111

all|83636

unadjustedvariance51.00

adjustmentforties-0.13

adjustmentforzeros-0.25

----------

adjustedvariance50.63

Ho:

x1=x2

z=1.405

Prob>

|z|=0.1599

，所以没有足够证据可以拒绝H0

例9－8某研究者欲了解不同受试者的血滤液在不同放置时间的血糖浓度，测定了8名正常人，将每位受试者的血滤液分成4份，然后随机地把它们放置0，45，90，135分钟，测定其血糖浓度，结果见表9－11。

表9－11不同放置时间的血滤液所含血液浓度（mg%）

放置时间（分）

135

95（3.5）

95（4）

106（4）

98（4）

102（4）

112（3.5）

105（4）

94（3）

105（3）

87

（1）

98（3）

112（3.5）

103（3）

92（3）

89

（2）

88

（2）

97

（2）

95（3）

101

（2）

90

（2）

83

（1）

81

（1）

90

（1）

90

（2）

88

（1）

94

（1）

80

（1）

Ri

23

95

106

98

102

105

94

87

97

101

83

80

具体分析步骤如下：

H0：

四个总体分布相同

H1：

四个总体分布不同或不全相同

swilkxifg==1对0时间资料进行正态性检验

Shapiro-WilkWtestfornormaldata

Variable|ObsWVzProb>

z

-------------+---------------------------------------------------------------------------------

x|80.934320.915-0.1410.55620

swilkxifg==2对45分钟时的资料进行正态性检验

Shapiro-WilkWtestfornormaldata

x|80.975250.345-1.5200.93570

swilkxifg==3对90分钟时的资料进行正态性检验

Variable|ObsWVzProb>

-------------+--------------------------------------------------------------------------------

x|80.870831.7991.0210.15358

swilkxifg==4对135分钟时的资料进行正态性检验

-------------+------------------------------------------------------------------------------

x|80.917111.1550.2360.40682

各组正态性检验的P值分别均大于α，所以可以按正态分布资料进行统计分析。

但是，对上面的数据进行方差齐性检验。

两因素方差分析

predicte,residual

将残差保存为e

genee=abs（e）

求e的绝对值，村为ee

anovaeegb

检验残差是否齐性

得到：

Numberofobs=32R-squared=0.6684

RootMSE=1.24825AdjR-squared=0.5105

Model|65.106.4.230.0026

g|15.35.3.320.0395

b|50.77.4.620.0029

Residual|32.211.

Total|98.313.

可见组间方差不齐，需要用非参数方法。

数据格式如下：

x3

x4

x5

x6

x7

x8

Stata程序为：

friedmanx1-x8

非参数检验

得到的结果为：

Friedman=19.5000

Kendall=0.8125

P-value=0.0002

Friedman检验p=0.0002，说明4个时间的血糖浓度不全相同。