小学奥数系列训练题乘法原理通用版Word文件下载.docx

小学奥数系列训练题乘法原理通用版Word文件下载.docx

《小学奥数系列训练题乘法原理通用版Word文件下载.docx》由会员分享，可在线阅读，更多相关《小学奥数系列训练题乘法原理通用版Word文件下载.docx（8页珍藏版）》请在冰豆网上搜索。

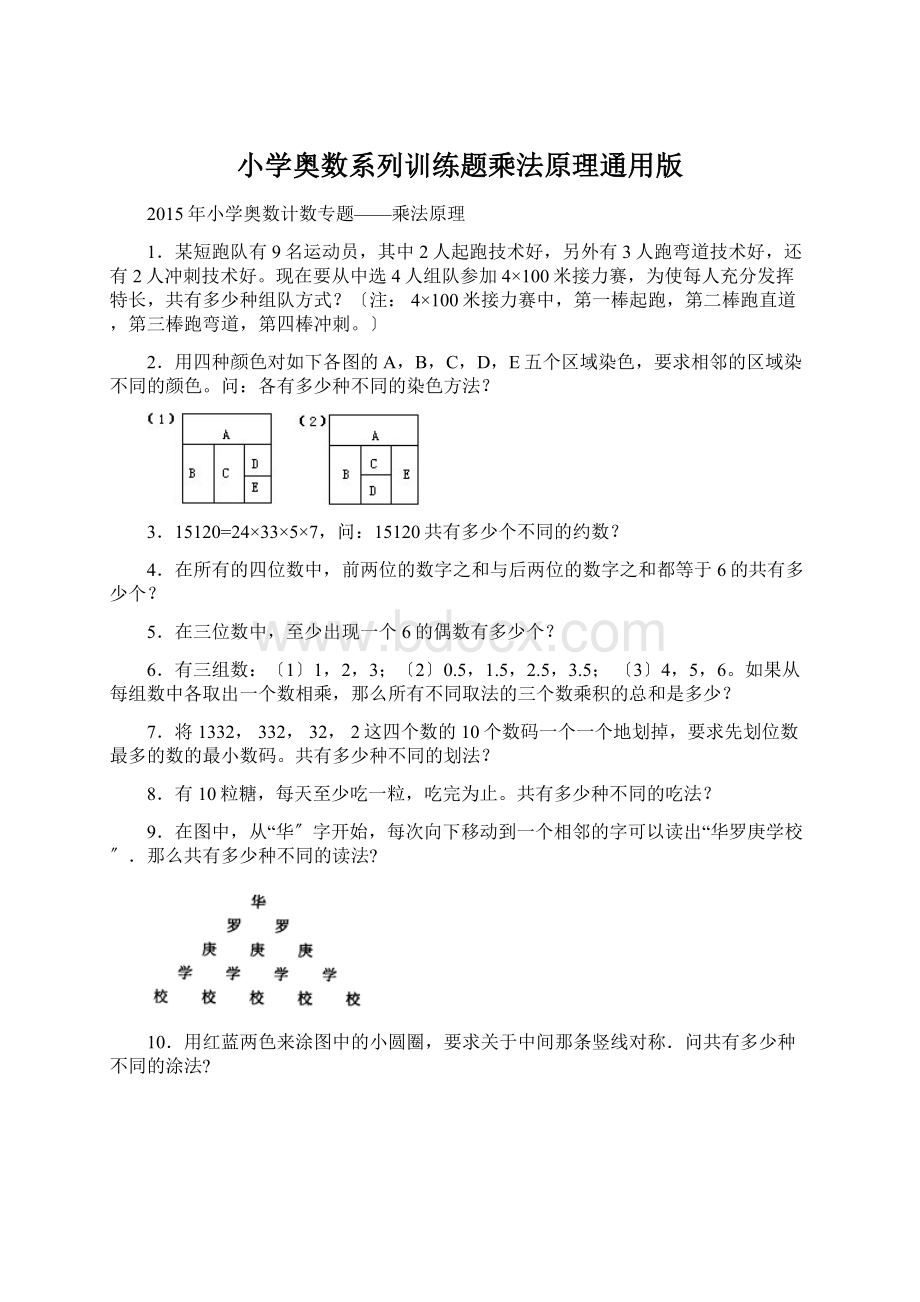
〔2〕0.5，1.5，2.5，3.5；

〔3〕4，5，6。

如果从每组数中各取出一个数相乘，那么所有不同取法的三个数乘积的总和是多少？

7．将1332，332，32，2这四个数的10个数码一个一个地划掉，要求先划位数最多的数的最小数码。

共有多少种不同的划法？

8．有10粒糖，每天至少吃一粒，吃完为止。

共有多少种不同的吃法？

9．在图中，从“华〞字开始，每次向下移动到一个相邻的字可以读出“华罗庚学校〞．那么共有多少种不同的读法?

10．用红蓝两色来涂图中的小圆圈，要求关于中间那条竖线对称．问共有多少种不同的涂法?

11．如图，把A，B，C，D，E这5局部用4种不同的颜色着色，且相邻的局部不能使用同一种颜色，不相邻的局部可以使用同一种颜色．那么，这幅图共有多少种不同的

着色方法?

12．图是一个中国象棋盘，如果双方准备各放一个棋子，要求它们不在同一行，也不在同一列，那么总共有多少种不同的放置方法?

13．在如下列图的阶梯形方格表的格子中放入5枚棋子，使得每行、每列都只有一枚棋子，那么这样的放法共有多少种?

14．有一种用六位数表示日期的方法是：

从左到右第一、二位数表示年，第三、四位数表示月，第五、六位数表示日，例如890817表示1989年8月17日．如果用这种方法表示1991年的日期，那么全年中6个数都不一样的日期共有多少天?

15．如果一个四位数与一个三位数的和是1999，并且四位数和三位数是由7个不同的数字组成的，那么这样的四位数最多能有多少个?

16．有五X卡片，分别写有1、2、4、5、8，现从中取出3X卡片，并排放在一起，组成一个三位数，问：

可以组成多少个不同的偶数？

17．五面五种颜色的小旗，任意取出一面、两面或三面排成一行表示各种信号，问：

可以表示成多少种不同的信号？

18．有大小不同的两个正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6，将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形？

19．有大小不同的两个正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6，将两个正方体放到桌面上，向上的一面数字之和为奇数的有多少种情形？

20．如如下图，有A、B、C、D、E五个区域，现有五种颜色给区域染色，染色要求：

每相邻两个区域不同色，每个区域染一色，有多少种不同的染色方式？

21．如如下图，有A、B、C、D、四个区域，现有四种颜色给区域染色，染色要求：

22．如如下图，有A、B、C、D、四个国家，现有红、黄、蓝三种颜色给地图染色，使相邻国家的颜色不同，但不是每种颜色都必须要用，问有多少种染色方式？

23．从1、3、5中任选2个数字，从2、4、6中任选2个数字，共可组成多少个没有重复数字的四位数?

24．一种拨号锁有4个拨号盘，每个拨号盘上有从0到9共10个数字，这4个拨号盘可以组成多少个四位数？

25．在小于10000的自然数中，含有数字1的数有多少个？

26．共有4×

4=16个方格，要把A，B,C,D四个不同的棋子放在方格里，并使每行每列只能出现一个棋子，问共有多少种不同的放法？

27．2003年12月6日0时起，某某市从7位升至8位。

由于特殊需要，电信部门一直有这样的规定：

普通市内的首位数字不使用0，1，9。

升位前某某市普通的容量为多少门？

升位后，某某市内的容量增加了多少门？

参考答案

1．72

【解析】起跑、弯道、冲刺各选1人后，还有6人可以跑直道。

2．96

【解析】〔1〕按A，B，C，D，E次序染色，可供选择的颜色依次有4，3，2，2，2种。

〔2〕按A，B，E，C，D次序染色，B与E同色时有4×

3×

1×

2×

2=48〔种〕，B与E异色时有4×

1=24〔种〕，共有48+24=72〔种〕。

3．80

【解析】15120的约数都可以表示成2a×

3b×

5c×

7d的形式，其中a=0，1，2，3，4，b=0，1，2，3，c=0，1，d=0，1，即a，b，c，d的可能取值分别有5，4，2，2种，所以共有约数5×

4×

2=80〔个〕。

4．42

【解析】前两位有15，24，33，42，51，60六种，后两位增加一个06，所以共有6×

7=42〔个〕。

5．162

【解析】三位偶数共有450个。

先计算没有6的三位偶数的个数。

个位数有0，2，4，8四种，十位数除6外有9种，百位除6，0外有8种，故没有6的三位偶数有4×

9×

8＝288〔个〕。

6．720

【解析】〔1＋2＋3〕×

〔0.5＋1.5＋2.5＋3.5〕×

〔4＋5＋6〕=720。

7．96

【解析】先划掉1332中的1，剩下332，332，32，2四个数；

下次该划掉位数最多的332中的2，有2种不同的顺序，划掉后剩下33，33，32，2四个数；

再划掉32中的2后，两个33中的3有8种划掉的顺序，划掉后剩下3，3，3，2四个数；

再划掉2后，三个3有6种划掉的顺序。

根据乘法原理，共有不同的划法2×

8×

6=96〔种〕。

8．512

【解析】初看此题似乎觉得很好入手，比如可以按天数进展分类枚举：

1天吃完的有1种方法，这天吃10块；

2天吃完的有9种方法，10=1+9=2+8=……=9+1；

当枚举到3天吃完的时，情况就有点错综复杂了，叫人无所适从……所以我们必须换一种角度来思考．

不妨从具体的例子入手来分析，比如这10块糖分4天吃完：

第1天吃2块；

第2天吃3块；

第3天吃1块；

第4天吃4块．

我们可以将10个“○〞代表10粒糖，把10个“○〞排成一排，“○〞之间共有9个空位，假如相邻两块糖是分在两天吃的，就在其间画一条竖线（如如下图）．

○○|○○○|○|○○○○

比如上图就表示“第1天吃2块；

第4天吃4块．〞

这样一来，每一种吃糖的方法就对应着一种“在9个空位中插入假如干个‘|’的方法〞，要求有多少个不同的吃法，就是要求在这9个空位中插入假如干个“|〞的方法数。

由于每个空位都有画‘|’与“不画‘|’两种可能：

根据乘法原理，在这9个空位中画假如干个“|〞的方法数有：

，这也就说明吃完10颗糖共有512种不同的吃法。

9．16

【解析】

从“华〞到“罗〞有2种读法；

而从“罗〞读到“庚〞，每个“罗〞有2种读法；

而从“庚〞读到“学〞，每个“庚〞有2种读法；

从“学〞到“校〞，每个“学〞有2种读法．

显然是分步进展的，适用乘法原理，于是满足题意的读法有2×

2＝16种．

10．128

注意到图中的竖线位置上的5个小圆圈，每个圆圈有2种涂法，而左、右两边，当一边确定后，另一边必须与这边对称，也就确定了，所以只用考虑某一侧，这样有2个圆圈，每个圆圈有2种涂法，所以共有2×

2＝128种不同的涂法．

11．96

A有4种着色方法；

A着色后，B有3种着色方法；

A、B着色后，C有2种着色方法；

A、B、C着色后，D有2种着色方法；

然后E有2种着色方式．

所以，共有4×

2＝96种不同的着色方法．

12．6480

设甲方先放棋子，乙方后放棋子．那么甲方可以把棋子放在棋盘的任意位置，故甲方有10×

9＝90种不同的放置方法．

对应甲方的第一种放法，乙方按规定必须去掉甲方棋子所在的行与列，而放置在剩下的任意位置，所以乙方有9×

8＝72种不同的放置方法．

所以，共有72×

90＝6480种不同的放置方法．

13．16

【解析】

第一列有2种方法，第一列放定后，第二列又有2种方法，…，如此下去，共有2×

1＝16种不同的放法．

14．30

第1、2位分别为9、1，故第3位不能为1，而只能为0．

由于第6位不能再为0、1，故第5位不能为3，当然，第5位也不能为0，1．

于是，这样的日期是910□2□的形式．

第4位可取3～8中的任一个，有6种方法．第3位取定后，第6位有5种取法．从而，共有6×

5＝30种，即全年中六个数字都不一样的日期有30天．

15．168

四位数的千位数字是1，百位数字a可在0、2、3、4、5、6、7中选择，这时三位数的百位数字是9－a；

四位数的十位数字b可在剩下的6个数字中选择，三位数的十位数字是9－b．

四位数的个位数字c可以在剩下的4个数字中选择，三位数的个位数字是9－c．

因此，所说的四位数有7×

6×

4＝168个．

16．3×

3=36

【解析】简单的乘法原理，以此判断出个位、十位、百位有几种选法。

17．5+5×

4+5×

3=85

【解析】同例2，分3类，再找每一类里的方法数。

18．18

【解析】奇数+奇数=偶数，偶数+偶数=偶数。

分这两类。

19．18

【解析】奇数+偶数=奇数，偶数+奇数=奇数。

20．420

【解析】根据B、D的染色是同色还是异色分两类。

21．84

【解析】根据A、D的染色是同色还是异色分两类。

22．18

【解析】根据B、C的染色是同色还是异色分两类。

23．216

【解析】从1、3、5中任选2个数字共有3种组合，从2、4、6中任选2个数字共有3种组合，再把选出的4个数进展排列，即可得出答案.

1=216（个）。

24．10000

【解析】每个拨号盘上的数字有10种取法，根据分步计数原理，4个拨号盘上各取1个数字组成的四位数字的个数是四个10相乘，所以，可以组成10000个四位数

25．3438

【解析】不妨将1至9999的自然数均看作四位数，凡位数不到四位的自然数在前面补0．使之成为四位数．

先求不含数字1的这样的四位数共有几个，即有0，2，3，4，5，6，7，8，9这九个数字所组成的四位数的个数．由于每一位都可有9种写法，所以，根据乘法原理，由这九个数字组成的四位数个数为

9=6561，

所以比10000小的不含数字1的自然数的个数是6561，于是，小于10000且含有数字1的自然数共有9999-6561=3438个．

26．576

【解析】从运用乘法原理，把放棋子的过程分为三个步骤：

第一步：

放棋子A。

棋子A可以任意放，有16种放法。

〔如如下图一〕

第二步：

放棋子B。

棋子B不能放在棋子A所在的行或列，对应棋子A的每一种放法，棋子B都可以放在剩下的9个方格的任意一格里，有9种放法。

〔如如下图二〕

第三步：

放棋子C。

棋子C不能放在棋子A、B所在的行或列，对应前面的每一种放法，棋子C可以放在剩下的4个方格的任意一格里，有4种放法。

〔如如下图三〕

第四步：

放棋子D。

棋子D不能放在棋子A、B、C所在的行或列，对应前面的每一种放法，棋子D都只有1种放法。

〔如如下图四〕

所以，四颗棋子共有不同的放法：

16×

1=576〔种〕

27．7000000,63000000

【解析】从由0～9共10个数字组成，数字可以重复使用。

升位前的7位，首位数字不使用0，1，9，共有7种不同的选择，第二、三、四、五、六、七位数字都有10种不同选择。

总容量为：

7×

10×

10=7000000〔门〕。

同理可算出，升位后8位总容量为：

10=80000000〔门〕。

升位后，某某市内的容量增加了：

80000000－7000000=63000000〔门〕。