答案-高中数学必做100题--数学3.doc

答案-高中数学必做100题--数学3.doc

《答案-高中数学必做100题--数学3.doc》由会员分享，可在线阅读，更多相关《答案-高中数学必做100题--数学3.doc（5页珍藏版）》请在冰豆网上搜索。

高中数学必做100题—必修3

班级：

姓名：

（说明：

《必修3》部分共精选8题，“◎”表示教材精选，“☆”表示《精讲精练.必修3》精选）

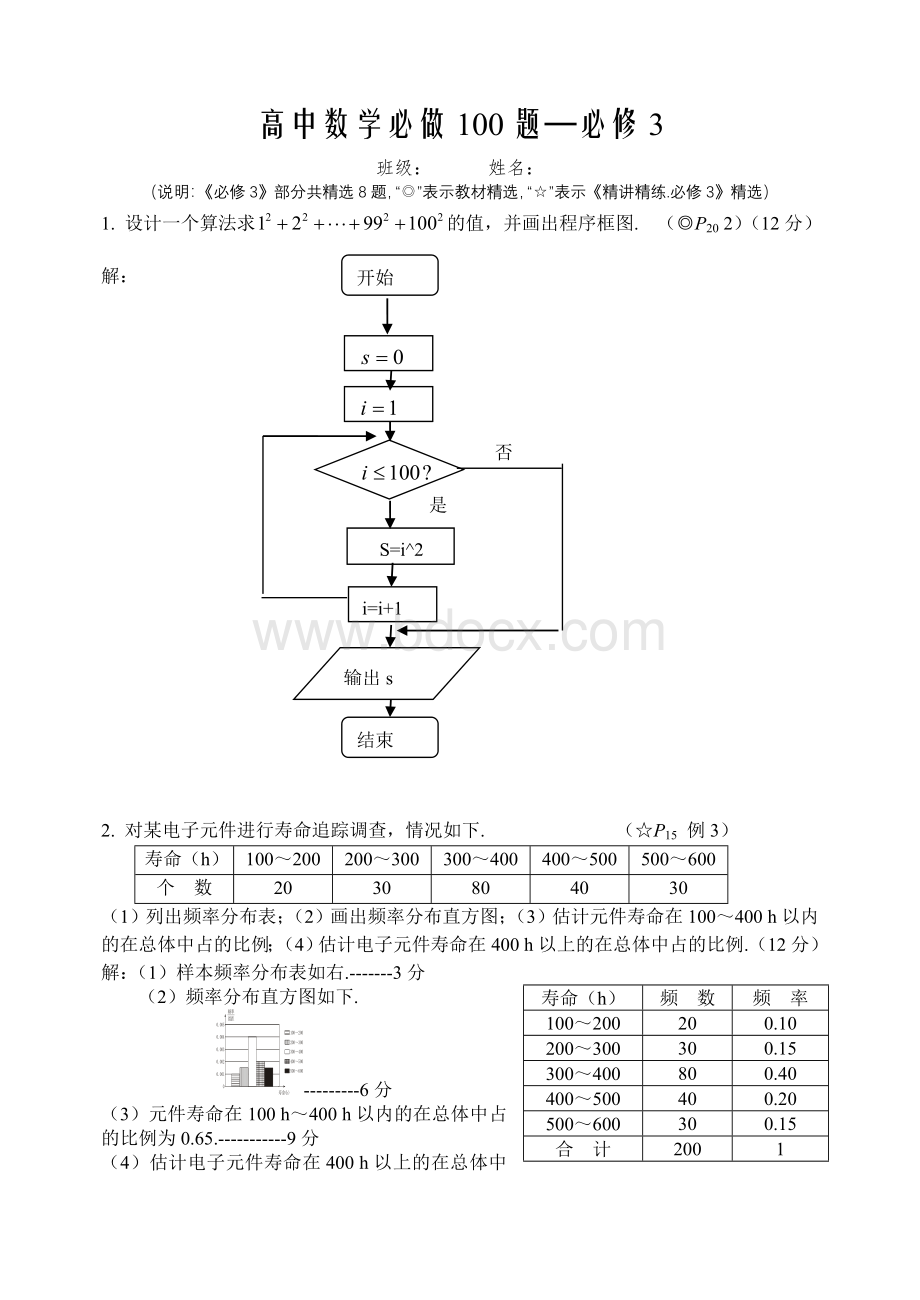
1.设计一个算法求的值，并画出程序框图.（◎P202）（12分）

开始

解：

否

是

S=i^2

i=i+1

输出s

结束

2.对某电子元件进行寿命追踪调查，情况如下.（☆P15例3）

寿命（h）

100～200

200～300

300～400

400～500

500～600

个数

20

30

80

40

30

（1）列出频率分布表；

（2）画出频率分布直方图；（3）估计元件寿命在100～400h以内的在总体中占的比例；（4）估计电子元件寿命在400h以上的在总体中占的比例.（12分）

解：

（1）样本频率分布表如右.-------3分

寿命（h）

频数

频率

100～200

20

0.10

200～300

30

0.15

300～400

80

0.40

400～500

40

0.20

500～600

30

0.15

合计

200

1

（2）频率分布直方图如下.

---------6分

（3）元件寿命在100h～400h以内的在总体中占的比例为0.65.-----------9分

（4）估计电子元件寿命在400h以上的在总体中占的比例为0.35.---------------12分

3.甲、乙两种玉米苗中各抽10株，分别测得它们的株高如下（单位：

cm）：

（☆P17例3）

甲：

25414037221419392142

乙：

27164427441640401640

问：

（1）哪种玉米的苗长得高？

（2）哪种玉米的苗长得齐？

（12分）

解：

（1）,

.

，即乙种玉米的苗长得高.--------------6分

（2），

.

，即乙种玉米的苗长得高，甲种玉米的苗长得整齐.--------12分

4.假设关于某设备的使用年限x和所支出的维修费用y（万元），有如下的统计资料：

（☆P228）

x

2

3

4

5

6

y

2.2

3.8

5.5

6.5

7.0

若由资料可知y对x呈线性相关关系，试求：

（1）回归直线方程；

（2）估计使用年限为10年时，维修费用约是多少？

（参考：

）（12分）

解：

（1）

所以回归直线方程为----------9分

（2），即估计用10年时维修费约为12.38万元.----12分

5.在一次商贸交易会上，商家在柜台开展促销抽奖活动，甲、乙两人相约同一天上午去该柜台参与抽奖.

（1）若抽奖规则是从一个装有6个红球和4个白球的袋中无放回地取出2个球，当两个球同色时则中奖，求中奖概率；

（2）若甲计划在9：

00～9：

40之间赶到，乙计划在9：

20～10：

00之间赶到，求甲比乙提前到达的概率.（12分）

解：

（1）从袋中10个球中摸出2个，试验的结果共有（种）.

中奖的情况分为两种：

（i）2个球都是红色，包含的基本事件数为；

（ii）2个球都是白色，包含的基本事件数为.

所以，中奖这个事件包含的基本事件数为15+6=21.因此,中奖概率为.----5分

（2）设两人到达的时间分别为9点到10点之间的x分钟、y分钟.

用表示每次试验的结果，则所有可能结果为

；

记甲比乙提前到达为事件A，则事件A的可能结果为

.

如图所示，试验全部结果构成区域Ω为正方形ABCD.而事件A所构成区域是正方形内的阴影部分.

根据几何概型公式，得到

.

所以，甲比乙提前到达的概率为.------12分

6.（2008年韶关模拟）某校从参加高一年级期末考试的学生中抽出60名学生，将其成绩（均为整数）分成六段，…后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

（1）求第四小组的频率，并补全这个频率分布直方图；

（3）估计这次考试的及格率（60分及以上为及格）和平均分；

（3）从成绩是80分以上（包括80分）的学生中选两人，求他们选在同一组的概率.（12分）

解：

（1）因为各组的频率和等于1,故第四组的频率：

.

直方图如右所示.--------4分

（2）依题意，60及以上的分数所在的第三、四、五、六组，频率和为

.

所以，抽样学生成绩的合格率是%.

利用组中值估算抽样学生的平均分

＝＝71.

估计这次考试的平均分是71分.---------8分

（3），的人数是15，3.所以从成绩是80分以上（包括80分）的学生中选两人，他们选在同一组的概率为.--------12分

7.（08年广东卷.文）某初级中学共有学生2000名，各年级男、女生人数如下表：

初一年级

初二年级

初三年级

女生

373

x

y

男生

377

370

z

已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.

（1）求x的值；

（2）现用分层抽样的方法在全校抽取48名学生，问应在初三年级抽取多少名？

（3）已知y245,z245,求初三年级中女生比男生多的概率.（12分）

解：

（1），.-----4分

（2）初三年级人数为y＋z＝2000－（373＋377＋380＋370）＝500，

现用分层抽样的方法在全校抽取48名学生，应在初三年级抽取的人数为：

（名）.----------8分

（3）设初三年级女生比男生多的事件为A，初三年级女生男生数记为（y，z）；

由

（2）知，且，基本事件空间包含的基本事件有：

（245，255）、（246，254）、（247，253）、……（255，245）共11个.

事件A包含的基本事件有：

（251，249）、（252，248）、（253，247）、（254,246）、（255,245）共5个.

.---------12分

8.（09年广东卷.文）随机抽取某中学甲乙两班各10名同学，测量他们的身高（单位：

cm），获得身高数据的茎叶图如图.

（1）根据茎叶图判断哪个班的平均身高较高；

（2）计算甲班的样本方差；

（3）现从乙班这10名同学中随机抽取两名身高不低于173cm的同学，求身高为176cm的同学被抽中的概率.（12分）

解：

（1）由茎叶图可知：

甲班身高集中于之间，而乙班身高集中于之间.因此乙班平均身高高于甲班;-------4分

（2），

甲班的样本方差为

＝57.2---8分

（3）设身高为176cm的同学被抽中的事件为A；

从乙班10名同学中抽中两名身高不低于173cm的同学有：

（181，173）（181，176）

（181，178）（181，179）（179，173）（179，176）（179，178）（178，173）

（178,176）（176，173）共10个基本事件，而事件A含有4个基本事件.

.--------12分