人教版学年八年级上册期末检测题及答案Word文档格式.docx

人教版学年八年级上册期末检测题及答案Word文档格式.docx

《人教版学年八年级上册期末检测题及答案Word文档格式.docx》由会员分享，可在线阅读，更多相关《人教版学年八年级上册期末检测题及答案Word文档格式.docx（13页珍藏版）》请在冰豆网上搜索。

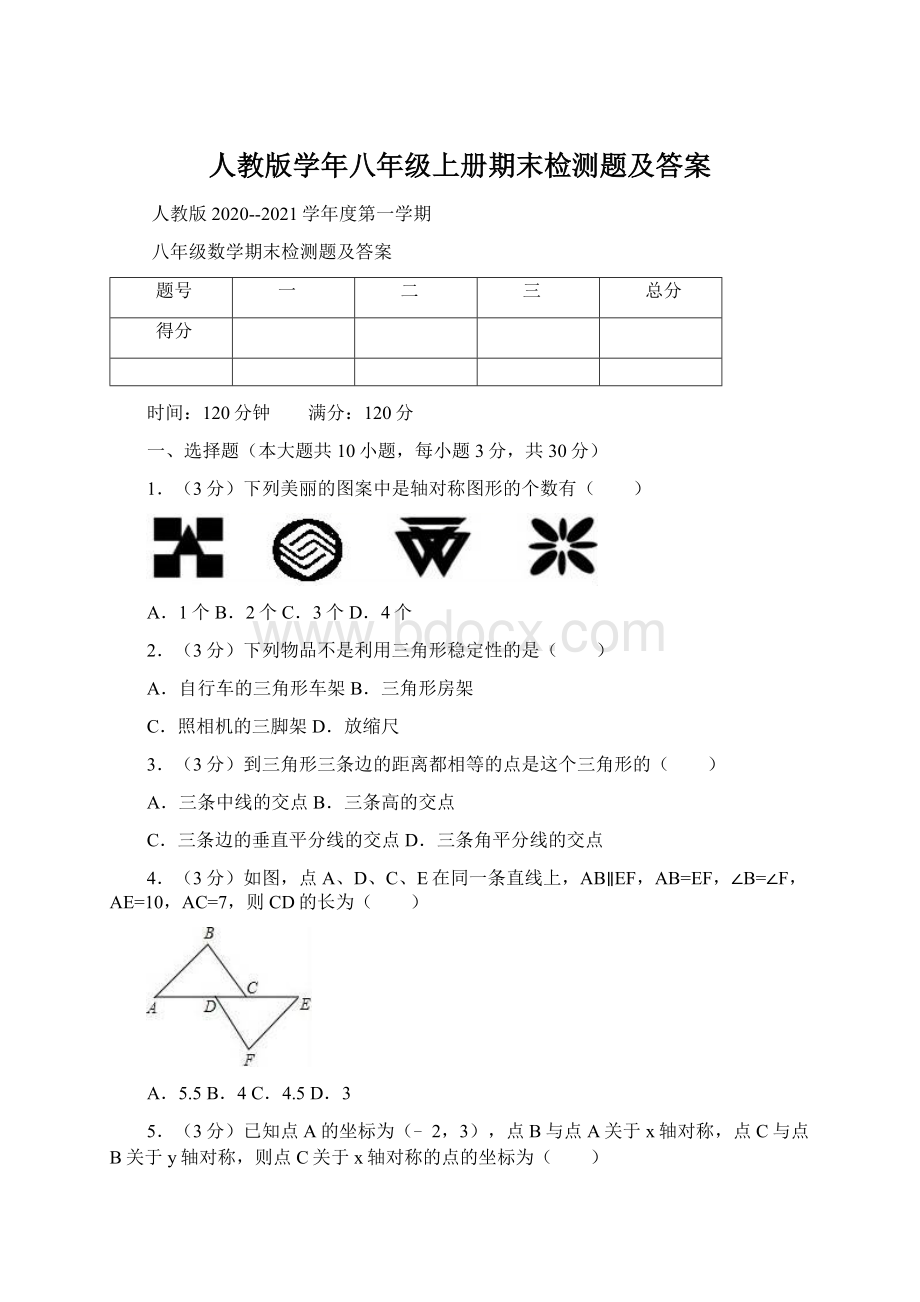
中的x和y都扩大2倍，则分式的值（　　）

A．扩大4倍B．扩大2倍C．不变D．缩小2倍

7．（3分）下列计算正确的是（　　）

A．x4•x4=x16B．（a3）2•a4=a9

C．（ab2）4÷

（﹣ab）2=﹣ab4D．（a﹣1b3）2=

8．（3分）如果分式

的值为零，那么x等于（　　）

A．1B．﹣1C．0D．±

1

9．（3分）若分式

，则分式

的值等于（　　）

A．﹣

B．

C．﹣

D．

10．（3分）如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作正三角形ABC和正三角形CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：

①AD=BE；

②PQ∥AE；

③AP=BQ；

④DE=DP；

⑤∠AOB=60°

．其中正确的结论的个数是（　　）

A．2个B．3个C．4个D．5个

二、填空题：

（本大题共6个小题，每小题3分，共18分）请将每小题正确答案写在题中横线上

11．（3分）在△ABC中，∠A=60°

，∠B=40°

，则∠C的度数是　　．

12．（3分）若x2+mx+n分解因式的结果是（x+2）（x﹣1），则m+n的值为　　．

13．（3分）a+b=2，ab=﹣2，则a2+b2=　　．

14．（3分）若2m=a，32n=b，m，n为正整数，则23m+10n=　　．

15．（3分）如图，∠AOB=30°

，∠AOB内有一定点P，且OP=12，在OA上有一点Q，OB上有一点R，若△PQR周长最小，则最小周长是　　．

16．（3分）在等腰△ABC中，AB=AC，一边上的中线BD将这个三角形的周长分为15和12两个部分，则该等腰三角形的底边长为　　．

三、简答题：

（本大题共9个小题，共72分）解答应写出演算步骤或文字说明，并将答案写在对应的答题区域内

17．（8分）分解因式：

（1）81x4﹣16；

（2）8ab3+2a3b﹣8a2b2

18．（6分）化简求值：

（x﹣y+

）（x+y﹣

），其中x=97，y=3．

19．（8分）解方程：

（1）

=

；

（2）

﹣

20．（6分）在创建文明城市的进程中，我市为美化城市环境，计划种值树木60万棵，由于志愿者的加入，实际每天植树比原计划多20%，结果提前5天完成任务，求原计划每天植树多少万棵？

21．（8分）如图，在△ABC中，BD平分∠ABC，

（1）作图：

作BC边的垂直平分线分别交BC，BD于点E，F（用尺规作图法，保留作图痕迹，不要求写作法）；

（2）在

（1）的条件下，连接CF，若∠A=60°

，∠ABD=24°

，求∠ACF的度数．

22．（8分）如图，BD是△ABC的角平分线，DE⊥AB，DF⊥BC，垂足分别为E，F

（1）求证：

BE=BF；

（2）若△ABC的面积为70，AB=16，DE=5，求BC的长．

23．（8分）如图1，在四边形ABCD中，DC∥AB，AD=BC，BD平分∠ABC．

AD=DC；

（2）如图2，在上述条件下，若∠A=∠ABC=60°

，过点D作DE⊥AB，过点C作CF⊥BD，垂足分别为E、F，连接EF．判断△DEF的形状并证明你的结论．

24．（8分）在Rt△ABC中，∠ACB=90°

，AC=BC，CD是∠ACB的角平分线，点E，F分别是边AC，BC上的动点，AC=4，设AE=x，BF=y．

（1）若x+y=3，求四边形CEDF的面积；

（2）当DE⊥DF时，如图2，试探索x、y之间的数量关系．

25．（12分）如图1所示，在Rt△ABC中，∠C=90°

，点D是线段CA延长线上一点，且AD=AB，点F是线段AB上一点，连接DF，以DF为斜边作等腰Rt△DFE，连接EA，EA满足条件EA⊥AB．

（1）若∠AEF=20°

，∠ADE=50°

，BC=2，求AB的长度；

（2）求证：

AE=AF+BC；

（3）如图2，点F是线段BA延长线上一点，探究AE、AF、BC之间的数量关系，并证明你的结论．

参考答案

1．C．2．D．3．D．4．B.5．C．6．B．7．D．8．B．9．B．10．C．

11．80°

．12．﹣1．13．8．14．a3b2．15．12.16．7或11．

17．

【解答】解：

（1）原式=（9x2+4）（9x2﹣4）

=（9x2+4）（3x+2）（3x﹣2）；

（2）原式=2ab（4b2+a2﹣4ab）

=2ab（a﹣2b）2．

18．

原式=

•

=（x+y）（x﹣y）=x2﹣y2，

当x=97，y=3时，原式=972﹣32=（97+3）×

（97﹣3）=100×

94=940．

19．

（1）去分母，得：

2x=5（x﹣3），

去括号，得：

2x=5x﹣15，

移项，合并同类项，得：

3x=15，

∴x=5，

经检验，x=5是原方程的解，

∴x=5；

（2）去分母，得：

3（3x﹣1）﹣6×

2=5，

9x﹣3﹣12=5，

9x=20，

∴x=

，

经检验，x=

是原方程的解，

．

20．

设原计划每天植树x万棵，则实际每天植树1.2x万棵，

根据题意得：

=5，

解得：

x=2，

经检验，x=2是原方程的解，且符合题意．

答：

原计划每天植树2万棵．

21．

（1）BC边的垂直平分线EF如图所示；

（2）∵BD平分∠ABC，∠ABD=24°

∴∠FBC=24°

∵EF垂直平分BC，

∴BF=CF，

∴∠FCB=∠FBC=24°

在△FDC中，∠FDC=∠A+∠ABD=60°

+24°

=84°

∠DFC=∠FCB+∠FBC=24°

=48°

∴∠ACF=180°

﹣84°

﹣48°

22．

（1）∵DE⊥AB，DF⊥BC，

∴∠BED=∠BFD=90°

∵BD是△ABC的角平分线，

∴∠EBD=∠FBD，

在△BDE和△BDF中，

∵

∴△DBE≌△DBF（AAS），

∴BE=BF；

（2）∵BD是△ABC的角平分线，DE⊥AB，DF⊥BC，

∴DF=DE=5，

∴S△ABD=

AB•DE=40，

∴S△BCD=

BC•DF=70﹣40=30，

∴BC=12．

23．

【解答】

（1）证明：

∵DC‖AB，

∴∠CDB=∠ABD，

又∵BD平分∠ABC，

∴∠CBD=∠ABD，

∴∠CDB=∠CBD，

∴BC=DC，

又∵AD=BC，

∴AD=DC；

（2）△DEF为等边三角形，

证明：

∵BC=DC（已证），CF⊥BD，

∴点F是BD的中点，

∵∠DEB=90°

，∴EF=DF=BF．

∵∠ABC=60°

，BD平分∠ABC，∴∠BDE=60°

∴△DEF为等边三角形．

24．

（1）在图1中，过点D作DG⊥AC于点G，DH⊥BC于点H．

∵∠ACB=90°

，AC=BC，CD是∠ACB的角平分线，

∴∠A=∠B=∠ACD=∠BCD=45°

∴AD=CD=BD．

∵在等腰直角三角形ACD中，DG⊥AC，∠A=45°

∴DG=AG=

AC=2，

同理：

DH=2．

∵S△CDE=

CE•DG=4﹣x，S△CDF=

CF•DH=4﹣y，

∴S四边形CEDF=S△CDE+S△CDF=（4﹣x）+（4﹣y）=8﹣（x+y）=5；

（2）当DE⊥DF时，∠EDF=90°

∵CD⊥AB，

∴∠ADE+∠EDC=∠EDC+∠CDF=90°

∴∠ADE=∠CDF．

在△ADE与△CDF中，

∴△ADE≌△CDF（ASA），

∴AE=CF，

∴AE+BF=CF+BF=BC，即x+y=4．

25．

（1）在等腰直角三角形DEF中，∠DEF=90°

∵∠1=20°

∴∠2=∠DEF﹣∠1=70°

∵∠EDA+∠2+∠3=180°

∴∠3=60°

∵EA⊥AB，

∴∠EAB=90°

∵∠3+∠EAB+∠A=180°

∴∠4=30°

∵∠C=90°

∴AB=2BC=4；

（2）如图1，过D作DM⊥AE于D，在△DEM中，∠2+∠5=90°

∵∠2+∠1=90°

∴∠1=∠5，

∵DE=FE，

在△DEM与△EFA中，

∴△DEM≌△EFA，

∴AF=EM，

∵∠4+∠B=90°

∵∠3+∠EAB+∠4=180°

∴∠3+∠4=90°

∴∠3=∠B，

在△DAM与△ABC中，

∴△DAM≌△ABC，

∴BC=AM，

∴AE=EM+AM=AF+BC；

（3）如图2，过D作DM⊥AE交AE的延长线于M，

∴∠1+∠B=90°

∵∠2+∠MAB+∠1=180°

，∠MAB=90°

∴∠2+∠1=90°

，∠2=∠B，

在△ADM与△BAC中，

∴△ADM≌△BAC，

∵EF=DE，∠DEF=90°

∵∠3+∠DEF+∠4=180°

∵∠3+∠5=90°

∴∠4=∠5，

在△MED与△AFE中，

∴△MED≌△AFE，

∴ME=AF，

∴AE+AF=AE+ME=AM=BC，

即AE+AF=BC．