学而思高中数学8-函数的概念.doc

学而思高中数学8-函数的概念.doc

《学而思高中数学8-函数的概念.doc》由会员分享，可在线阅读，更多相关《学而思高中数学8-函数的概念.doc（14页珍藏版）》请在冰豆网上搜索。

13

学而思教育

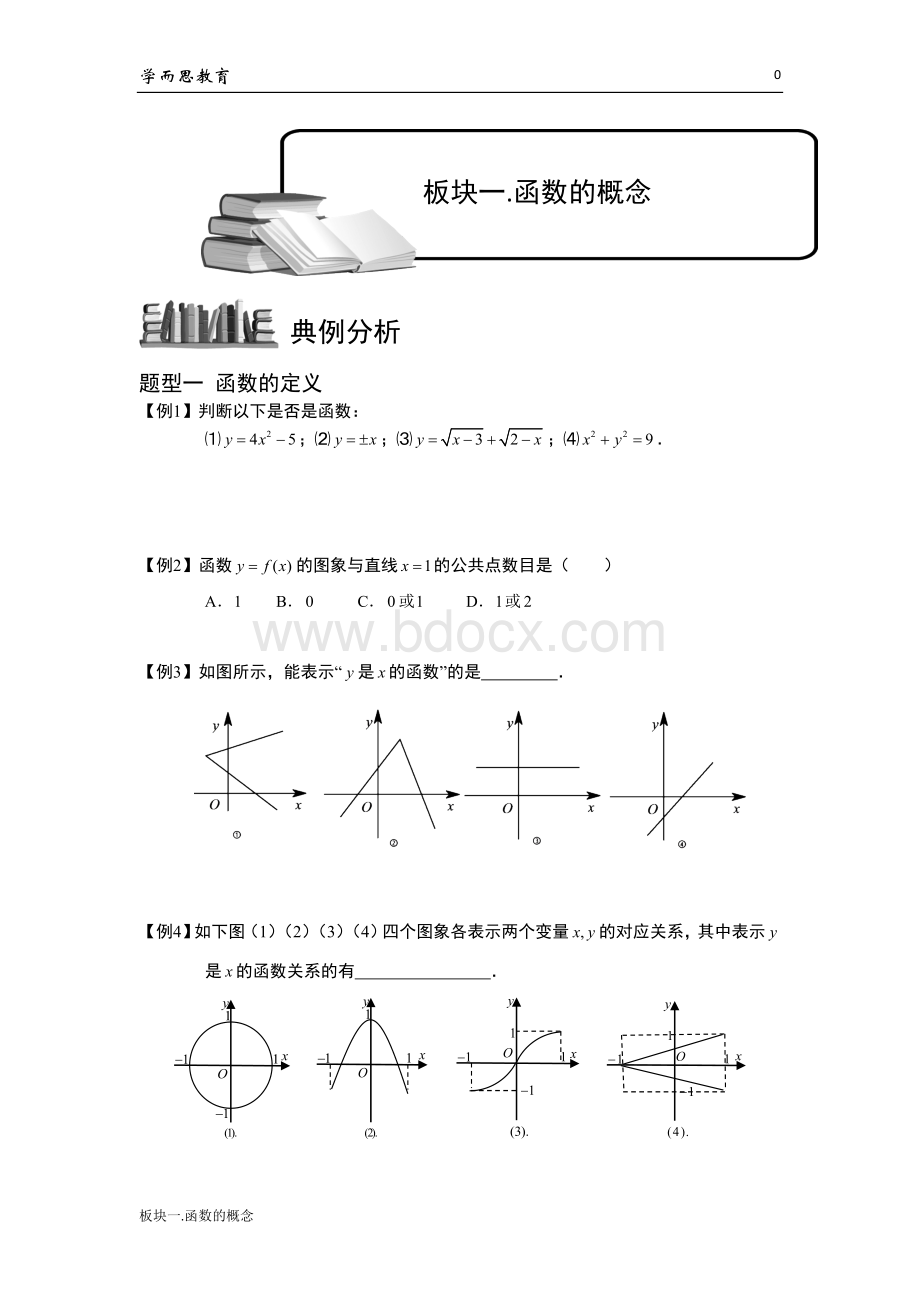
板块一.函数的概念

典例分析

题型一函数的定义

【例1】判断以下是否是函数：

⑴；⑵；⑶；⑷．

【例2】函数的图象与直线的公共点数目是（）

A．B．C．或D．或

【例3】如图所示，能表示“是的函数”的是．

【例4】如下图

（1）

（2）（3）（4）四个图象各表示两个变量的对应关系，其中表示是的函数关系的有．

【例5】给出下列四个图形，其中能表示从集合M到集合N的

函数关系的有（）

A、0个B、1个C、2个D、3个

x

x

x

x

1

2

1

1

1

2

2

2

1

1

1

1

2

2

2

2

y

y

y

y

3

O

O

O

O

【例6】以下给出的对应是不是从集合到集合的映射？

如果是映射，是不是一一映射．

⑴集合是数轴上的点，集合，对应关系：

数轴上的点与它所代表的实数对应；

⑵集合是平面直角坐标系中的点，集合，对应关系：

平面直角坐标系中的点与它的坐标对应；

⑶集合是三角形，集合是圆，对应关系：

每一个三角形都对应它的内切圆；

⑷集合是华星中学的班级，集合是华星中学的学生，对应关系：

每一个班级都对应班里的学生．

【例7】下列对应中有几个是映射？

【例8】已知，，则从到的不同映射共有（）

A．4个B．3个C．2个D．1个

【例9】设是集合A到B的映射，下列说法正确的是（）

A、A中每一个元素在B中必有象B、B中每一个元素在A中必有原象

C、B中每一个元素在A中的原象是唯一的D、B是A中所在元素的象的集合

【例10】⑴若集合，，：

A→B表示A到B的一个映射，且满足对任意都有为偶数，则这样的映射有_______个．

⑵设是从集合A到B的映射，，

，若B中元素在映射f下的原象是，

则k，b的值分别为________．

【例11】已知集合，，下列从A到B的对应不是映射的是（）

A．B．

C．D．

【例12】集合A={3，4}，B={5，6，7}，那么可建立从A到B的映射个数是__________，从B到A的映射个数是__________.

【例13】已知集合，且使中元素和中的元素对应，则的值分别为（）

A．B．C．D．

【例14】（09年山东梁山）设f、g都是由A到A的映射，其对应法则如下表（从上到下）：

映射f的对应法则是表1

原象

1

2

3

4

象

3

4

2

1

映射g的对应法则是表2

原象

1

2

3

4

象

4

3

1

2

则与相同的是（）

A．；B．；C．；D．

【例15】（07年北京）已知函数，分别由下表给出

1

2

3

1

3

1

1

2

3

3

2

1

则的值为 ；满足的的值是

【例16】（06陕西）为确保信息安全，信息需加密传输，发送方由明文密文（加密），接收方由密文明文（解密），已知加密规则为：

明文对应密文例如，明文对应密文当接收方收到密文时，则解密得到的明文为（）

A．；B．；C．；D．

【例17】已知，规定到的一个映射为=，

⑴如果，求；

⑵如果，求；

⑶如果，求．

题型二函数的定义域

【例18】求下列函数的定义域

（1）；

（2）；（3）.

【例19】求下列函数的定义域：

（1）；

（2）.

【例20】函数的自变量的取值范围是（）

A．B．C．D．且

【例21】函数的定义域．

【例22】函数的定义域是___________．

【例23】求函数的定义域．

【例24】（2008年全国I卷文理）函数的定义域是（）

A．B．C．D．

【例25】求下列函数的定义域⑴；⑵；⑶．

【例26】若的定义域是，求的定义域．

【例27】已知函数定义域是，则的定义域是（）

A．B．C．D．

【例28】

（1）已知已知函数f（x）=的定义域是R，则实数a的取值范围是（）

A．a＞ B．－12＜a≤0 C．－12＜a＜0 D．a≤

【例29】

（1）求下列函数的定义域：

的定义域．

（2）已知函数的定义域是，求函数的定义域．

【例30】

（1）函数的定义域为,求函数的定义域;

（2）已知函数的定义域为,求的定义域;

（3）已知函数的定义域为,求的定义域.

【例31】求下述函数的定义域：

（1）；

（2）

【例32】已知函数定义域为（0，2），求下列函数的定义域：

（1）；

（2）。

题型三函数的值域

一、用非负数的性质

【例33】求下列函数的值域：

（1）y=-3x2+2;

（2）y=5+2（x≥-1）.

【例34】函数的最小值是_________________．

【例35】求函数的值域．

二、分离常数法

对某些分式函数，可通过分离常数法，化成部分分式来求值域．

【例36】求下列函数的值域：

（1）y=

（2）y=.

三、利用函数单调性

已知函数在某区间上具有单调性，那么利用单调性求值域是一种简单的方法．

【例37】求函数y=3x-的值域.

四、利用判别式

特殊地，对于可以化为关于x的二次方程a（y）x2+b（y）x+c（y）=0的函数y=f（x），可利用．

【例38】求函数y=的最值．

【例39】利用判别式方法求函数的值域．

五、利用数形结合

　　数形结合是解数学问题的重要思想方法之一，求函数值域时其运用也不例外．

【例40】若（x+）（y-）=0,求x-y的最大、最小值．

六、利用换元法求值域

　　有时直接求函数值域有困难，我们可通过换元法转化为容易求值域的问题考虑．

【例41】求函数y=2x-5+的值域．

七、利用反解函数求值域

　　因函数y=f（x）的值域就是反函数y=f-1（x）的定义域，故某些时候可用此法求反函数的值域．

【例42】求函数y=（x＞0）的值域．

八、利用已知函数的有界性．

【例43】求函数y=的值域.

九、求值域综合性题目．

【例44】求下列函数的值域：

⑴⑵⑶．

【例45】求下列函数的值域：

（1）；

（2）；（3）．

【例46】求下列函数的值域⑴；⑵．

【例47】求下列函数的值域：

（1）；

（2）；

（3）；（4）；

【例48】求下列函数的定义域与值域：

（1）；

（2）.

【例49】求下列函数的值域

⑴；⑵，；

⑶；⑷．

【例50】求下列函数的值域：

（1）；

（2）；（3）；

（4）；（5）；（6）；

（7）；（8）；（9）。

十、应用值域去未知系数取值范围．

【例51】设函数，若，则实数的取值范围是．

【例52】函数的值域是（）

A．B．C．D．

【例53】已知函数在区间[1，1]上的最小值为3，求实数的值．

【例54】已知函数f（x）=x2+mx–4在区间〔2，4〕上的两个端点取得最大的最小值。

（1）求m的取值范围；

（2）试写出最大值Y为m的函数关糸式;

（3）最大值Y是否存在最小值?

若有，请求出来；若无，请说明理由。

【例55】若一系列函数的解析式相同、值域相同,但其定义域不同,则称这些函数为“同族函数”,那么函数解析式为、值域为{1,4}的“同族函数”共有个.

【例56】已知函数

⑴求函数的定义域；

⑵求，的值；

⑶当时，求，的值．

【例57】已知函数，若，试求函数的值域.

【例58】已知xy＜0，并且4x-9y=36．由此能否确定一个函数关系y=f（x）？

如果能，求出其解析式、定义域和值域；如果不能，请说明理由．

【例59】函数的定义域为，值域为，

则满足条件的实数组成的集合是．

【例60】若函数的定义域为，值域为，则的取值范围是（）

A．B．C．D．

【例61】当时，函数取得最小值．

【例62】设函数，当时，的值有正有负，则实数的范围．

【例63】对于任意实数，函数恒为正值，求的取值范围．

【例64】记二次函数在的最大值为，写出的函数表达式，并求出的最小值．

题型三相等函数

【例65】试判断以下各组函数是否表示同一函数？

（1）f（x）=，g（x）=；

（2）f（x）=，g（x）=

（3）f（x）=，g（x）=（）2n－1（n∈N*）；

（4）f（x）=，g（x）=；

（5）f（x）=x2－2x－1，g（t）=t2－2t－1

【例66】下列各组函数中，与表示同一函数的一组是（　　）

A．　 B．，

C．， D．

【例67】判断下列各组中的两个函数是同一函数的为（）

⑴，；

⑵，；

⑶，；

⑷，；

⑸，．

A．⑴、⑵B．⑵、⑶C．⑷D．⑶、⑸

板块一.函数的概念