北师大版七下数学几何部分期末练习.doc

北师大版七下数学几何部分期末练习.doc

《北师大版七下数学几何部分期末练习.doc》由会员分享，可在线阅读，更多相关《北师大版七下数学几何部分期末练习.doc（19页珍藏版）》请在冰豆网上搜索。

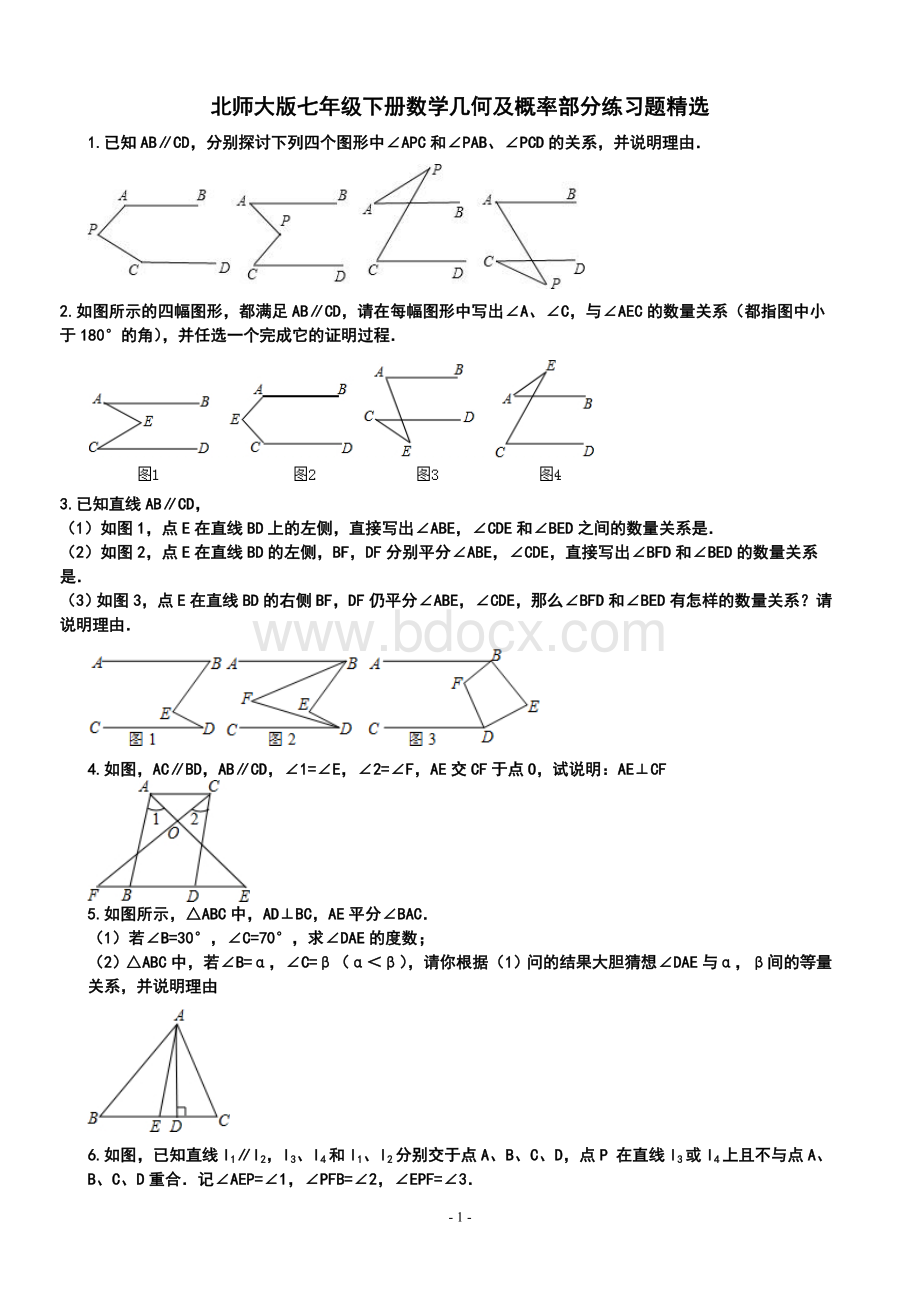
北师大版七年级下册数学几何及概率部分练习题精选

1.已知AB∥CD，分别探讨下列四个图形中∠APC和∠PAB、∠PCD的关系，并说明理由．

2.如图所示的四幅图形，都满足AB∥CD，请在每幅图形中写出∠A、∠C，与∠AEC的数量关系（都指图中小于180°的角），并任选一个完成它的证明过程．

3.已知直线AB∥CD，

（1）如图1，点E在直线BD上的左侧，直接写出∠ABE，∠CDE和∠BED之间的数量关系是．

（2）如图2，点E在直线BD的左侧，BF，DF分别平分∠ABE，∠CDE，直接写出∠BFD和∠BED的数量关系是．

（3）如图3，点E在直线BD的右侧BF，DF仍平分∠ABE，∠CDE，那么∠BFD和∠BED有怎样的数量关系？

请说明理由．

4.如图，AC∥BD，AB∥CD，∠1=∠E，∠2=∠F，AE交CF于点O，试说明：

AE⊥CF

5.如图所示，△ABC中，AD⊥BC，AE平分∠BAC．

（1）若∠B=30°，∠C=70°，求∠DAE的度数；

（2）△ABC中，若∠B=α，∠C=β（α＜β），请你根据

（1）问的结果大胆猜想∠DAE与α，β间的等量关系，并说明理由

6.如图，已知直线l1∥l2，l3、l4和l1、l2分别交于点A、B、C、D，点P在直线l3或l4上且不与点A、B、C、D重合．记∠AEP=∠1，∠PFB=∠2，∠EPF=∠3．

（1）若点P在图

（1）位置时，求证：

∠3=∠1+∠2；

（2）若点P在图

（2）位置时，请直接写出∠1、∠2、∠3之间的关系；

（3）若点P在图（3）位置时，写出∠1、∠2、∠3之间的关系并给予证明．

7.如图，直线AB与CD相交于点O，OE⊥CD．

（1）若∠BOD=28°，求∠AOE的度数．

（2）若OF平分∠AOC，小明经探究发现，当∠BOD为锐角时，∠EOF的度数始终都是∠BOC度数的一半，请你判断他的发现是否正确，并说明理由

8.情境观察：

如图1，△ABC中，AB=AC，∠BAC=45°，CD⊥AB，AE⊥BC，垂足分别为D、E，CD与AE交于点F．

①写出图1中所有的全等三角形；

②线段AF与线段CE的数量关系是．

问题探究：

如图2，△ABC中，∠BAC=45°，AB=BC，AD平分∠BAC，AD⊥CD，垂足为D，AD与BC交于点E．求证：

AE=2CD．拓展延伸：

如图3，△ABC中，∠BAC=45°，AB=BC，点D在AC上，∠EDC=∠BAC，DE⊥CE，垂足为E，DE与BC交于点F．求证：

DF=2CE．

9.如图，已知∠1+∠2=180°，∠3=∠B，试判断∠AED与∠C的大小关系，并对结论进行说理．

10.如图，在△ABC中，AB=AC，AD是BC边上的高，AM是△ABC外角∠CAE的平分线．

（1）用尺规作图方法，作∠ADC的平分线DN；（保留作图痕迹，不写作法和证明）

（2）设DN与AM交于点F，判断△ADF的形状，并证明你的结论

11.如图，在△ABC中，∠B=∠C，点F为AC上一点，FD⊥BC于D，过D点作DE⊥AB于E，若∠AFD=158°，求∠EDF的度数

12.

（1）探究：

如图1，求证：

∠BOC=∠A+∠B+∠C

（2）应用：

如图2，∠ABC=100°，∠DEF=130°，求∠A+∠C+∠D+∠F的度数

13.已知：

如图，在△ABC中，∠ABC=∠ACB，AD⊥BD，AE⊥CE，且AD=AE．求证：

△AEC≌△ADB

14.如图，点C在线段AB上，AD∥EB，AC=BE，AD=BC，CF平分∠DCE．试探索CF与DE的位置关系，并说明理由

15.如图，在等边△ABC中，点D为AC上一点，CD=CE，∠ACE=60°．

（1）求证：

△BCD≌△ACE；

（2）延长BD交AE于F，连接CF，若AF=CF，猜想线段BF、AF的数量关系，并证明你的猜想

16.如图，AD是△ABC的中线，BE⊥AD于点E，CF⊥AD交AD的延长线于点F．求证：

BE=CF

17.如图，△ABC是等边三角形，D是AC上一点，BD=CE，∠1=∠2，试判断BC与AE的位置关系，并证明你的结论

18.如图，已知∠MAN=120°，AC平分∠MAN，∠ABC+∠ADC=180°，求证：

①DC=BC；②AD+AB=AC

19.如图，在△ABC中，AB=CB，∠ABC=90°，D为AB延长线上一点，点E在BC边上，且BE=BD，连结AE、DE、DC．

①求证：

△ABE≌△CBD；

②若∠CAE=30°，求∠BDC的度数．

20.如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AB=CD，请你再添加个条件，使得AE=DF，并说明理．

21.已知：

如图，△ABC和△EFC都是等腰直角三角形，∠ACB=∠ECF=90°，点E在AB边上．

（1）求证：

△ACE≌△BCF；

（2）若∠BFE=60°，求∠AEC的度数

22.已知：

∠ACB=90°，AC=BC，AD⊥CM，BE⊥CM，垂足分别为D，E，

（1）如图1，

①线段CD和BE的数量关系是；

②请写出线段AD，BE，DE之间的数量关系并证明．

（2）如图2，上述结论②还成立吗？

如果不成立，请直接写出线段AD，BE，DE之间的数量关系．

23.已知：

如图，AE=CF，DE⊥AC，BF⊥AC，垂足分别为E，F，DE=BF．求证：

AB∥CD．

24.如图，已知AB⊥AC，AB=AC，DE过点A，且CD⊥DE，BE⊥DE，垂足分别为点D，E．求证：

△ADC≌△BEA

25.如图，△ABC中，AB=BC，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF

（1）求证：

△ABE≌△CBF；

（2）若∠BAE=25°，求∠ACF的度数．

26.在△ABC中，AB=AC，AD⊥BC于D，BE⊥AC于E，AE=BE．

求证：

（1）∠DAB=∠EBC；

（2）AF=2CD．

27.如图，AB∥ED，已知AC=BE，且点B、C、D三点共线，若∠E=∠ACB．求证：

BC=DE．

28.如图，在△ABC和△CED中，AB∥CD，AB=CE，AC=CD．求证：

∠B=∠E．

29.如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：

DE=DF

30.如图，AB=CB，BE=BF，∠1=∠2，证明：

△ABE≌△CBF．

31.如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：

△ACD≌△CBE．

32.已知：

如图，点A，D，C在同一直线上，AB∥EC，AC=CE，∠B=∠EDC．

求证：

BC=DE．

33.如图，∠BAC=∠DAE，∠ABD=∠ACE，AB=AC．求证：

BD=CE．

34.如图，D是△ABC的边AB上一点，DF交AC于点E，DE=FE，FC∥AB，求证：

AD=CF．

35.阅读发现：

（1）如图①，在Rt△ABC和Rt△DBE中，∠ABC=∠DBE=90°，AB=BC=3，BD=BE=1，连结CD，AE．易证：

△BCD≌△BAE．（不需要证明）

提出问题：

（2）在

（1）的条件下，当BD∥AE时，延长CD交AE于点F，如图②，求AF的长．

解决问题：

（3）如图③，在Rt△ABC和Rt△DBE中，∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，连结CD，AE．当∠BAE=45°时，点E到AB的距离EF的长为2，求线段CD的长为

36.已知：

如图，在△ABC中，∠ACB=90°，点D在BC上，且BD=AC，过点D作DE⊥AB于点E，过点B作CB的垂线，交DE的延长线于点F．求证：

AB=DF．

37.如图，已知∠ABC=90°，D是AB延长线上的点，AD=BC，过点A作AF⊥AB，并截取AF=BD，连接DC、DF、CF，求证：

FD⊥CD．

38.如图，请你在下列各图中，过点P画出射线AB或线段AB的垂线．

39.如图

（1），由三角形的内角和或外角和可知：

∠ABC=∠A+∠C+∠O在图

（2）中，直接利用上述的结论探究：

①若AD、CD分别平分∠OAB，∠OCB，且∠O=80°∠B=120°，求∠ADC的度数

②AD、CD分别平分∠OAB，∠OCB，猜想∠O，∠ABC，∠ADC之间的等量关系，并说明理由．

40.已知：

如图，点B在线段AD上，BC∥DE，AB=ED，BC=DB．求证：

∠A=∠E

41.如图，在Rt△ABC和Rt△ADE中，AB=AC，AD=AE，CE与BD相交于点M，BD交AC于点N．试猜想BD与CE有何关系？

并证明你的猜想

42.如图，已知CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，且OB=OC．求证：

AO平分∠BAC

43.已知：

如图，在△ABC中，AB=AC，∠BAC=90°，点D是BC的中点，点E，F分别在AB，AC边上，连接DE，DF，∠EDF=90°，求证：

BE=AF

44.如图：

△ABC和△ADE均为等腰直角三角形，且∠BAC=∠DAE=90°，点B，C，E在同一条直线上，连结DC．

（1）请找出图中的全等三角形，并给予证明（说明：

结论中不得含有未标识的字母）；

（2）证明：

DC⊥BE．

45.探究：

（1）如图1，在ABC与ADE中，AB=AC，AD=AE，∠BAC=∠DAE=90°，连结BD、CE．请写出图1中所有全等的三角形：

（不添加字母）．

（2）如图2，已知△ABC，AB=AC，∠BAC=90°，l是过A点的直线，CN⊥l，BM⊥l，垂足为N、M．求证：

△ABM≌△CAN．

解决问题：

（3）如图3，已知△ABC，AB=AC，∠BAC=90°，D在边BC上，DA=DE，∠ADE=90°，求证：

AC⊥CE．

46.已知：

如图，EF⊥BC于点F，ED⊥AB于点D交BC于点M，BD=EF．求证：

BM=EM

47.如图，在△ABC的外部，分别以AB、AC为直角边，点A为直角顶点，作等腰直角△ABD和等腰直角△ACE，CD与BE交于点P．

试证：

（1）CD=BE；

（2）∠BPC=90°

48.如图

（1），△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，AD⊥MN于点D，BE⊥MN于点E．

（1）请说明：

△ADC≌△CEB．

（2）请你探索线段DE，AD，EB间的等量关系，并说明理由；

（3）当直线MN绕点C旋转到图

（2）的位置时，其它条件不变，线段DE，AD，EB又有怎样的等量关系？

（不必说理由）．

49.

（1）如图①∵∠B+∠D+∠1=180°

又∵∠1=∠A+∠2

∠2=∠C+∠E

∴∠A+∠C+∠E+∠B+∠D=180°

（2）将图①变形成图②，∠A+∠DBE+∠C+∠D+∠E仍然为180°，请证明这个结论．

（3）将图①变形成图③，则∠A+∠B+∠C+∠D+∠E还为180°，请继续证明这个结论．

50.如图，在Rt△ABC中，∠ACB=90°，∠A=22.5°，斜边AB的垂直平分线交AC于点D，点F在AC上，点E在BC的延长线上，CE=CF，连接BF，DE．线段DE和BF在数量和位置上有什么关系？

并说明理由

51.如图，在△ABC中，AC边的垂直平分线DM交AC于D，BC边的垂直平分线EN交BC于E，DM与EN相交于点F

（1）若△CMN的周长为20cm，求AB的长；

（2）若∠MFN=70°，求∠MCN的度数

52.在△ABC中，AD是高，在线段DC上取一点E，使BD=DE，已知AB+BD=DC，

求证：

E点在线段AC的垂直平分线上

53．如图，已知：

E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足