直角三角形边角关系知识点教学内容Word文档下载推荐.docx

直角三角形边角关系知识点教学内容Word文档下载推荐.docx

《直角三角形边角关系知识点教学内容Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《直角三角形边角关系知识点教学内容Word文档下载推荐.docx（8页珍藏版）》请在冰豆网上搜索。

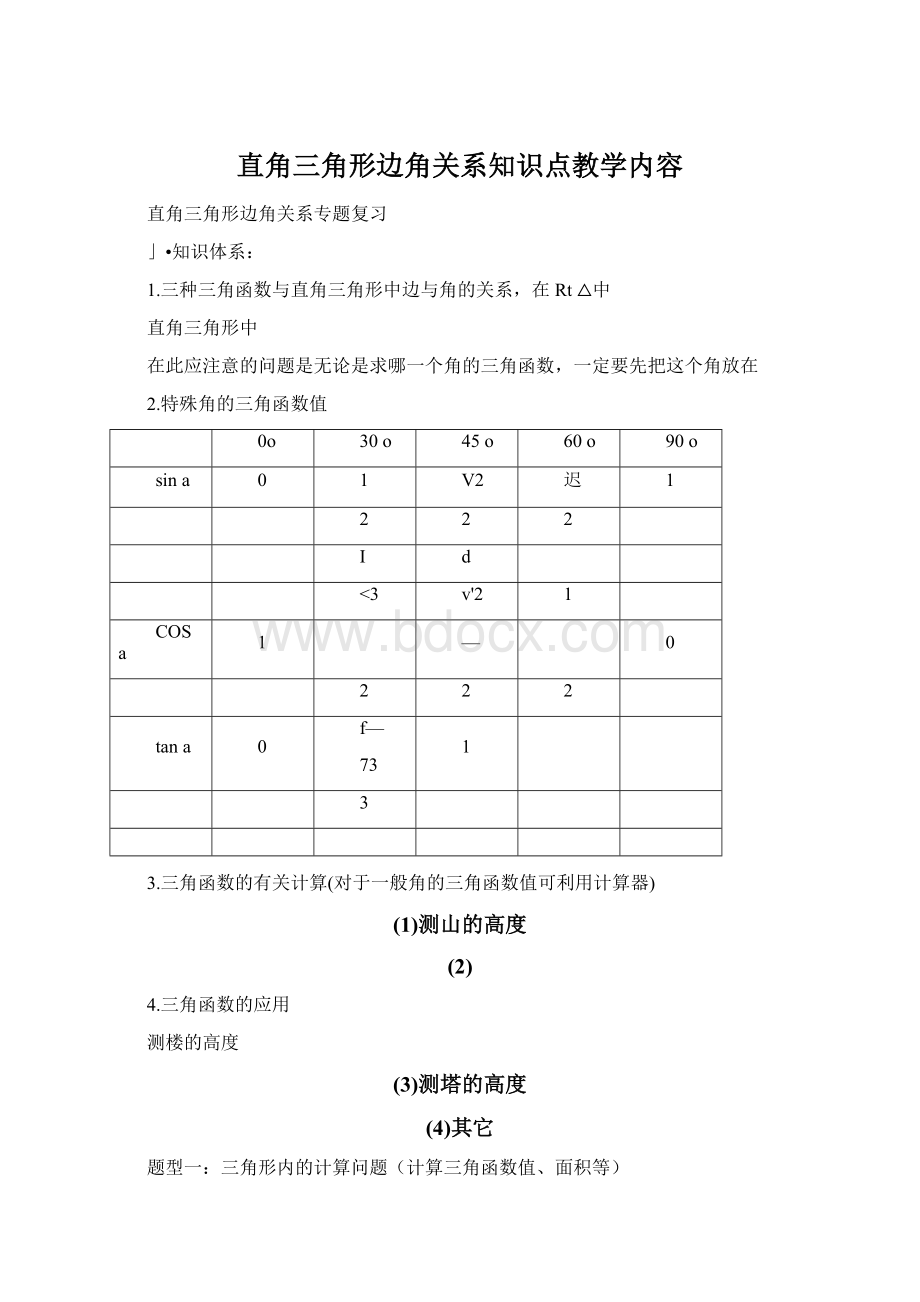
d

<

3

v'

COSa

—

tana

f—

73

3.三角函数的有关计算（对于一般角的三角函数值可利用计算器）

（1）测山的高度

（2）

4.三角函数的应用

测楼的高度

（3）测塔的高度

（4）其它

题型一：

三角形内的计算问题（计算三角函数值、面积等）

例2.已知，四边形

ABCD中，/ABC=/ADB=90°

AB=5,AD=3,BC=2.3，求四边形

ABCD的面

例1.在RtABC中，/0=90°

，且sinA-,AB=3,求BC,AC及B.2

例3.如图，在RtABC中，BCA90,CD是中线，BC5,CD4，求AC的长。

A

变式训练:

1、

RtABC中，/

C=90°

AC=4BC=3

cosB的值为

【

】

1r

C

B

、

、-D、

5

4

2、

在菱形ABCD中,

/ABC=60

AC=4,

贝UBD的长是

、8.3B

、4._3

、2、.3D

、8

3、

在RtABC中，/

/C=90°

tanA=3,

AC-1Q贝USLabc等于•

A、3B、300C、D150

4、在Rt△ABC中，如果各边长度都扩大为原来的2倍，那么锐角A的正弦值（）

A.扩大2倍B.缩小2倍C.扩大4倍D.没有变化

是【】

a

A、acsinBB、accosBC、cd、casinA

5、在RtABC中，/C=90°

ZA、/B、/C的对边分别为a、b、c三边，则下列式子一定成立的

tanB

6、等腰三角形的腰长为10cm顶角为120，此三角形面积为。

7、在RtABC中，/C=90°

CD是AB边上的中线，BC=8CD=5,则tanACD。

&

在ABC中，若C90,sinA,AB2，则ABC的周长为

9、已知菱形ABCD勺边长为6,/A=600,如果点P是菱形内一点，且PB=PD=23，那么AP的长为

10、某村计划开挖一条长1500米的水渠，渠道的断面为等腰梯形，渠道深0.8米，下底宽1.2米，坡角为450（如图所示），求挖土多少立方米。

题型二：

化简求值问题

例3.计算2cos30tan45tan60（、.21）0

1、化简

sin30

tan60

sin60

2、若

A是锐角，

cosA

—,则sin（90A）

3、若

迈，则A

4、tan30（tan1525'

19"

）。

5、计算:

2cos301

sin30cos4522

（1）

（2）（tan45）、.cos30

（3）3tan30

6、计算：

sin35cos55

2sin60

cos60sin45

题型三：

三角函数应用问题

（1）楼层问题：

1、如图，甲楼每层高都是3.1米，乙楼高40米，从甲楼的第6层往外看乙楼楼顶，仰角为30，两楼相距护*

有多远？

（结果精确到0.1米）/

2、如图，气象大厦离小伟家80米，小伟从自家的窗中眺望大厦，并测得大厦顶部的仰角是42，而大厦

底部的俯角是34，求该大厦的高度（结果精确到0.1米）

3、如图11为住宅区内的两幢楼，它们的高AB=CD=30m两楼间的距离A（=24m,现需了解甲楼对乙楼采光

的影响情况•当太阳光与水平线的夹角为30°

时，求甲楼的影子在乙楼上有多高？

（2）航行问题：

1、如图，某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处，经16小时的航行到达，

到达后必须立即卸货，此时接到气象部门通知，一台风中心正以40海里/时的速度由A向北偏西60°

方向

乙

移动，距台风中心200海里的圆形区域（包括边界）均会受到影响。

（1）问B处是否会受到影响？

请说明理由。

（2）为避免受到台风的影响，该船应在多少小时内卸完货物。

2、一艘船由A港沿东偏北30方向航行20千米至B港，然后再沿东偏南60方向航行20千米至C港，求:

（1）A,C两港之间的距离（结果精确到0.1千米）

（2）确定C港在A港的什么方位？

（5分）

3、如图，一条渔船某时刻在位置A观测灯塔BC（灯塔B距离A处较近），两个灯塔恰好在北偏东65°

45'

的方向上，渔船向正东方向航行I小时45分钟之后到达D点，观测到灯塔B恰好在正北方向上，已知两个

灯塔之间的距离是12海里，渔船的速度是16海里/时，又知在灯塔C周围18.6海里内有暗礁，问这条渔船按原来的方向继续航行，有没有触礁的危险？

东

（3）仰角问题:

1、一天在升旗时小苏发现国旗升至5米高时，在她所站立的地点看国旗的仰角是45，当国旗升至旗杆顶

端时国旗的仰角恰为60，小苏的身高是1米6，则旗杆高米。

（将国旗视作一点,保留根号）

2、如图，RtABC是一防洪堤背水波的横截面图，斜坡AB的长为13米，它的坡角为45，为了提高防洪

堤的防洪能力，现将背水坡改造成坡比1:

1.5的斜坡AD求DB的长（结果保留根号）（6分）

3、如图，为测得峰顶A到河面B的高度h,当游船行至C处时测得峰顶A的仰角为a,前进m米至D处时测得峰顶A的仰角为B（此时C、DB三点在同一直线上）.

（1）用含a、B和m的式子表示h;

⑵当a=45°

3=60°

m=50米时，求h的值.

]）C

（精确到0.1m，•-、2〜1.41,.3〜1.73）

4、如图湖泊的中央有一个建筑物

向行100m到D点，又测得其顶部

AB,某人在地面C处测得其顶部A的仰角为60°

然后，自C处沿BC方

A的仰角为30°

，求建筑物的高（结果保留根号）

1、如图，B,C是河岸边两点，A是对岸边上的

一点，测得ABC30，

ACB60，BC50米,

则A到岸边BC的距离是米。

2、如图2,沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工.从

AC上的一点B,取

/ABD145°

BD=500米，/D=55°

，要使A,C,E成一直线，那么开挖点E离点D的距离是（）

A.500sin55。

米B.500cos55。

米C.500tan55。

米D.500tan35。

米

|?

12

（1）sin450-cos60°

+tan600;

（2）sin12330°

+cos230°

-tan450;

（3）sin300-tan30°

+cos45°