苏科版七年级数学下第一次月考复习题汇编一含答案Word格式文档下载.docx

苏科版七年级数学下第一次月考复习题汇编一含答案Word格式文档下载.docx

《苏科版七年级数学下第一次月考复习题汇编一含答案Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《苏科版七年级数学下第一次月考复习题汇编一含答案Word格式文档下载.docx（15页珍藏版）》请在冰豆网上搜索。

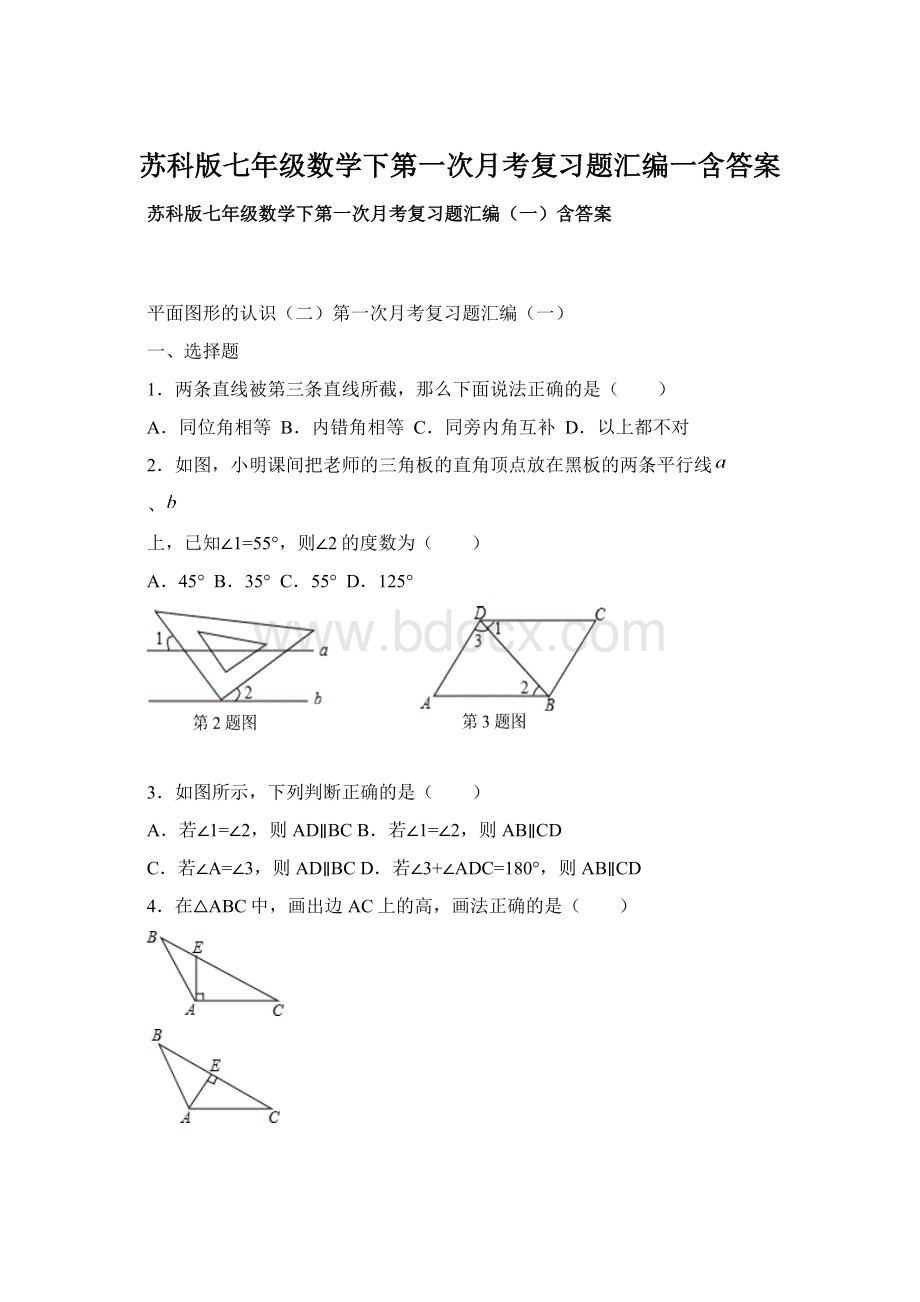
A．右转80°

B．左转80°

C．右转100°

D．左转100°

9．如图，AD是△ABC的角平分线，点O在AD上，且OE⊥BC于点E，∠BAC=60°

，∠C=80°

，则∠EOD的度数为（　　）

A．20°

B．30°

C．10°

D．15°

10．下列长度的三根木棒首尾相接，能做成三角形框架的是（　）

A．1cm、2cm、3cmB．2cm、3cm、4cm

C．3cm、5cm、8cmD．4cm、5cm、10cm

二、填空题

11．一个凸多边形每一个内角都是135°

，则这个多边形是边形．

12．已知竖直方向的线段AB长为6cm，如果AB沿水平方向平移8cm，那么线段AB扫过的区域的面积是cm2．

13．珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同，如图，若∠ABC=120°

，∠BCD=80°

，则∠CDE=度．

第14题图

第15题图

第13题图

14．如图，已知△ABC的∠ABC和∠ACB的平分线BE，CF交于点G，若∠BGC=115°

，则∠A=．

15．如图，某同学剪了两片角度均为50°

的硬板纸纸片（∠BAC=∠EDF=50°

），将其中一片平移，连结AD，如果△AGD中有两个角相等，则∠GAD的度数为．

16．在下列语句中：

①由∠A：

∠B：

∠C=4：

3：

2可确定△ABC是锐角三角形；

②若三角形的两边长是3和4，且周长是偶数，则这个三角形的第三边是3或5；

③一个图形和它经过平移所得的图形中，两组对应点的连线互相平行；

④若一个多边形的外角和是内角和的

，则这个多边形是十二边形．

其中正确的是（只要写序号）．

17．十二边形的外角和是　　°

．

18．一个三角形的两边长为8和10，则它的最长边的取值范围是________．

19．如图，三角形ABE向右平移一定距离后得到三角形CDF，若∠BAE＝60°

，∠B＝25°

，则∠ACD＝______．

第19题图

第20题图

20．一个小区大门的栏杆如图所示，BA垂直地面AE于A，CD平行于地面AE，那么∠ABC＋∠BCD=度．

三、解答题

21．如图，△ABC的顶点都在方格纸的格点上，将△ABC向右平移4格，再向上平移2格，其中每个格子的边长为1个单位长度．

（1）在图中画出平移后的△A′B′C′；

（2）若连接AA′、CC′，则这两条线段的关系是；

（3）利用格点作直线MN，将△ABC分成面积相等的三角形．

22．如图，在△ABC中，∠B=50°

，∠AEC=80°

，CE平分∠ACB，求∠A和∠BCE的度数．

23．如图，△ABC中，点D、E在边AB上，点F在边BC上，点G在边AC上，EF、CD与BG交于M、N两点，∠ADG=50°

，∠ACB=60°

（1）若∠BMF+∠GNC=180°

，CD与EF平行吗？

为什么？

（2）在

（1）的基础上，若∠GDC=∠EFB，试求∠A的度数．

24．如图，△ABC中，AD⊥BC于点D，BE平分∠ABC，若∠EBC=32°

，∠AEB=70°

（1）求∠BAD和∠CAD的度数；

（2）若点F为线段BC上的任意一点，当△EFC为直角三角形时，求∠BEF的度数．

25．如图1，已知线段AB、CD相交于点O，连接AC、BD，我们把形如图1的图形称之为“8字形”．如图2，∠CAB和∠BDC的平分线AP和DP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：

（1）仔细观察，在图2中有个以线段AC为边的“8字形”；

（2）在图2中，若∠B=96°

，∠C=100°

，求∠P的度数．

（3）在图2中，若设∠C=α，∠B=β，∠CAP=

∠CAB，∠CDP=

∠CDB，试问∠P与∠C、∠B之间存在着怎样的数量关系（用α、β表示∠P），并说明理由；

（4）如图3，则∠A+∠B+∠C+∠D+∠E+∠F的度数为．

26．一个多边形的外角和等于内角和的

，求这个多边形的边数．

27．如图，在△BCD中，BC=4，BD=5．

（1）求CD的取值范围；

（2）若AE∥BD，∠A=55°

，∠BDE=125°

，求∠C的度数．

28．如下图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．将△ABC向左平移2格，再向上平移4格．

（1）请在图中画出平移后的△A′B′C′；

（2）再在图中画出△A′B′C′的高C′D′，并求出△ABC的面积．

29．如图，∠A＝∠C＝90°

，BE，DF分别为∠ABC与∠ADC的平分线，能判断BE∥DF吗？

试说明理由．

30．若∠C=α，∠EAC+∠FBC=β

（1）如图①，AM是∠EAC的平分线，BN是∠FBC的平分线，若AM∥BN，则α与β有何关系？

并说明理由．

（2）如图②，若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P，试探究∠APB与α、β的关系是　　　　　　．（用α、β表示）

（3）如图③，若α≥β，∠EAC与∠FBC的平分线相交于P1，∠EAP1与∠FBP1的平分线交于P2；

依此类推，则∠P5=　　　　　　．（用α、β表示）

参考答案

题号

1

2

3

4

5

6

7

8

9

10

答案

D

B

C

A

11．八12．4813．2014．50°

15．50°

或80°

或65°

16．

17．36018．

19．25°

20．270

21．

（1）如图所示，△A′B′C′即为所求；

（2）平行且相等；

（3）如图所示，直线MN即为所求

22．∵∠B=50°

，

∴∠BCE=∠AEC-∠B=30°

∵CE平分∠ACB，

∴∠BCA=2∠BCE=60°

∴∠A=180°

-∠B-∠BCA=70°

23．

（1）∵∠BMF+∠GNC=180°

，∠BMF+∠NMF=180°

∴∠GNC=∠NMF，

∴CD∥EF；

（2）∵CD∥EF，

∴∠DCB=∠EFB，

∵∠GDC=∠EFB，

∴∠DCB=∠GDC，

∴DG∥BC，

∴∠ADG=∠ABC=50°

，∠AGD=∠ACB=60°

-50°

-60°

=70°

24．

（1）证明：

∵BE平分∠ABC，

∴∠ABC=2∠EBC=64°

∵AD⊥BC，

∴∠ADB=∠ADC=90°

∴∠BAD=90°

-64°

=26°

∵∠C=∠AEB-∠EBC=70°

-32°

=38°

∴∠CAD=90°

-38°

=52°

；

（2）解：

分两种情况：

①当∠EFC=90°

时，如图1所示：

则∠BFE=90°

∴∠BEF=90°

-∠EBC=90°

=58°

②当∠FEC=90°

时，如图2所示：

则∠EFC=90°

∴∠BEF=∠EFC-∠EBC=52°

=20°

综上所述：

∠BEF的度数为58°

或20°

25．

（1）3；

（2）∵∠CAB和∠BDC的平分线AP和DP相交于点P，

∴∠CAP=∠BAP，∠BDP=∠CDP，

∵∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，

∴∠C-∠P=∠P-∠B，

即∠P=

（∠C+∠B），

∵∠C=100°

，∠B=96°

∴∠P=

（100°

+96°

）=98°

（3）∠P=

（β+2α）；

理由：

∵∠CAP=

∠CDB，

∴∠BAP=

∠BAC，∠BDP=

∠BDC，

∴∠C-∠P=

∠BDC-

∠BAC，∠P-∠B=

∠BAC，

∴2（∠C-∠P）=∠P-∠B，

（∠B+2∠C），

∵∠C=α，∠B=β，

（4）如右图，∵∠B+∠A=∠1，∠C+∠D=∠2，

∴∠A+∠B+∠C+∠D=∠1+∠2，

∵∠1+∠2+∠F+∠E=360°

∴∠A+∠B+∠C+∠D+∠E+∠F=360°

故答案为：

360°

26．解：

设这个多边形的边数为

依题意得：

°

解得

答：

这个多边形的边数为9．

27．解：

（1）∵在△BCD中，BC=4，BD=5，

∴1＜DC＜9；

（2）∵AE∥BD，∠BDE=125°

∴∠AEC=55°

又∵∠A=55°

∴∠C=70°

28．解：

（1）如图1；

（2）如图2，

∵A′B′=4，C′D′=4，

∴S△A′B′C′=

A′B′×

C′D′=

×

4×

4=8，

∵△A′B′C′由△ABC平移而成，

∴S△ABC=S△A′B′C′=8．

29．解：

BE∥DF．

∵∠A=∠C=90°

∴∠ABC+∠ADC=180°

∵BE，DF分别为∠ABC与∠ADC的平分线，

∴∠ABE=

∠ABC，∠ADF=

∠ADC，

∴∠ABE+∠ADF=90°

∵∠ABE+∠AEB=90°

∴∠AEB=∠ADF，

∴BE∥DF．

30．解：

（1）∵AM是∠EAC的平分线，BN是∠FBC的平分线，

∴∠MAC+∠NCB=

∠EAC+

∠FBC=

β，

∵AM∥BN，

∴∠C=∠MAC+∠NCB，

即α=

β；

（2）∵∠EAC的平分线与∠FBC平分线相交于P，

∴∠PAC+∠PBC=

∴∠C=∠APB+（∠PAC+∠PBC），

∴α=∠APB+

即∠APB=α－

（3）由

（2）得，∠P1=∠C-（∠PAC+∠PBC）=α－

∠P2=∠P1-（∠P2AP1+∠P2BP1），

=α－

β－

β=α－

∠P3=α－

∠P4=α－

∠P5=α－

β．