人口指数增长模型和Logistic模型Word文档格式.docx

人口指数增长模型和Logistic模型Word文档格式.docx

《人口指数增长模型和Logistic模型Word文档格式.docx》由会员分享，可在线阅读，更多相关《人口指数增长模型和Logistic模型Word文档格式.docx（10页珍藏版）》请在冰豆网上搜索。

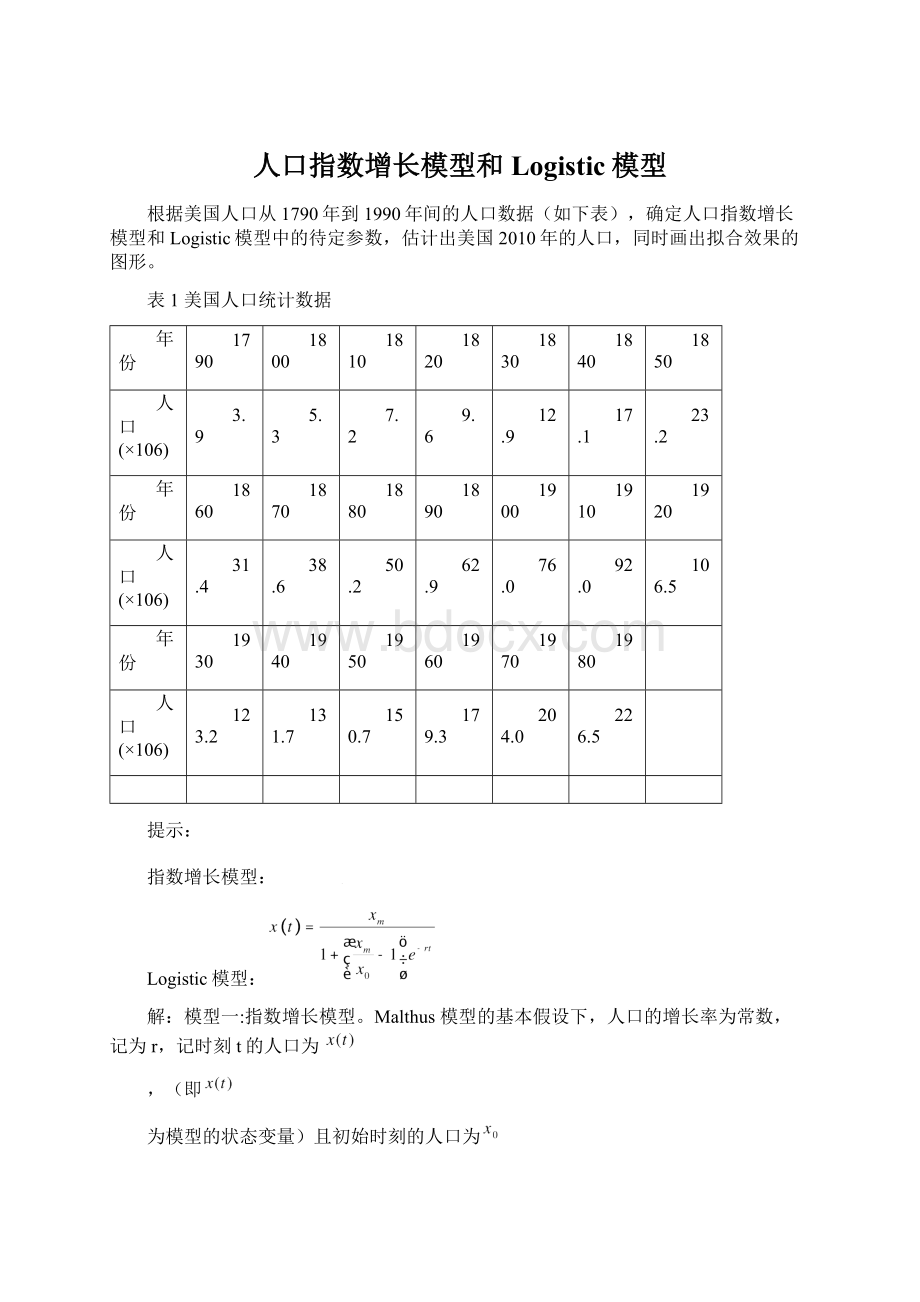
1910

1920

31.4

38.6

50.2

62.9

76.0

92.0

106.5

1930

1940

1950

1960

1970

1980

123.2

131.7

150.7

179.3

204.0

226.5

提示：

指数增长模型：

Logistic模型：

解：

模型一:

指数增长模型。

Malthus模型的基本假设下，人口的增长率为常数，记为r，记时刻t的人口为

，（即

为模型的状态变量）且初始时刻的人口为

，因为

由假设可知

经拟合得到：

程序：

t=1790:

10:

1980;

x（t）=[3.95.37.29.612.917.123.231.438.650.262.976.092.0106.5123.2131.7150.7179.3204.0226.5];

y=log（x（t））;

a=polyfit（t,y,1）

r=a

（1）,x0=exp（a

（2））

x1=x0.*exp（r.*t）;

plot（t,x（t）,'

r'

t,x1,'

b'

）

结果：

a=0.0214-36.6198

r=0.0214

x0=1.2480e-016

所以得到人口关于时间的函数为：

，其中x0=1.2480e-016，

输入：

t=2010;

x0=1.2480e-016;

x（t）=x0*exp（0.0214*t）

得到x（t）=598.3529。

即在此模型下到2010年人口大约为598.3529

。

模型二：

阻滞增长模型（或Logistic模型）由于资源、环境等因素对人口增长的阻滞作用，人口增长到一定数量后，增长率会下降，假设人口的增长率为x的减函数，如设

，其中r为固有增长率（x很小时），

为人口容量（资源、环境能容纳的最大数量），于是得到如下微分方程：

建立函数文件curvefit_fun2.m

functionf=curvefit_fun2（a,t）

f=a

（1）./（1+（a

（1）/3.9-1）*exp（-a

（2）*（t-1790）））;

在命令文件main.m中调用函数文件curvefit_fun2.m

%定义向量（数组）

x=1790:

1990;

y=[3.95.37.29.612.917.123.231.438.650.262.976...

92106.5123.2131.7150.7179.3204226.5251.4];

plot（x,y,'

*'

x,y）;

%画点，并且画一直线把各点连起来

holdon;

a0=[0.001,1];

%初值

%最重要的函数，第1个参数是函数名（一个同名的m文件定义），第2个参数是初值，第3、4个参数是已知数据点

a=lsqcurvefit（'

curvefit_fun2'

a0,x,y）;

disp（['

a='

num2str（a）]）;

%显示结果

%画图检验结果

xi=1790:

5:

2020;

yi=curvefit_fun2（a,xi）;

plot（xi,yi,'

）;

%预测2010年的数据

x1=2010;

y1=curvefit_fun2（a,x1）

holdoff

运行结果：

a=311.95310.02798178

y1=267.1947

其中a

（1）、a

（2）分别表示

中的

和

，y1则是对美国美国2010年的人口的估计。

第二题：

问题重述：

一垂钓俱乐部鼓励垂钓者将钓上的鱼放生，打算按照放生的鱼的重量给与鼓励，俱乐部只准备了一把软尺用于测量，请你设计按照测量的长度估计鱼的重量的方法。

假定鱼池中只有一种鲈鱼，并且得到8条鱼的如下数据（胸围指鱼身的最大周长）：

身长（cm）

36.8

31.8

43.8

32.1

45.1

35.9

重量（g）

765

482

1162

737

1389

652

454

胸围（cm）

24.8

21.3

27.9

21.6

22.9

问题分析：

鲈鱼的体重主要与鱼的身长、胸围有关系。

一般来说，鲈鱼的胸围越大，鱼的体重会越重，身长越长，体重也越重。

但鱼的胸围与身长之间又有些必然的联系，共同影响鱼的体重。

建模的目的是寻求鲈鱼体重与身长、胸围之间的数量规律

模型假设：

1、鲈鱼的身长越长体重越重，体重与身长存在正相关关系；

2、鲈鱼的胸围越大体重也越重，体重与胸围存在正相关的关系；

3、鲈鱼的胸围、身长互相影响，共同作用鲈鱼的体重；

4、鲈鱼的形态近似为与胸围等周长与身长等高的圆柱体。

符号说明：

鲈鱼的身长

鲈鱼的胸围

鲈鱼的体重

模型的建立及求解：

（一）、鲈鱼体重与身长模型的确立

为了研究鲈鱼身长与体重的关系，我们利用已测量的数据，取出身长及体重的数据，利用MATLAB软件画出散点图，如下：

从图形上看，鲈鱼的体重与身长可能是二次函数关系，我们利用多项式拟合的方法，得到：

（1）

根据拟合的函数，我们画出拟合图：

从拟合图上看，大部分原始数据在拟合函数附近，说明用二次函数拟合的效果较好，下面利用得出的函数对鱼的体重进行估计，用相对误差检验拟合度，得到下表：

表一、鲈鱼体重实际值与估计值对比及误差表

拟合值（g）

466.6

479.9

674.4

727.3

1228.8

1339.4

相对误差（%）

3.2

0.44

5.7

3.44

4.93

5.75

3.57

0.86

从表中的数据，我们可以得出鲈鱼体重的实际值与估计值的相对误差不大，说明用二次函数拟合鲈鱼身长与体重的关系式可行的。

（二）、鲈鱼体重与胸围的模型确立

仅仅考虑鲈鱼胸围对体重的影响，我们采用与模型一相同的方法，先画出鲈鱼体重与胸围的散点图：

从图形上看，鲈鱼体重与胸围可能成线性关系，利用多项式拟合的方法，我们得到鲈鱼体重与胸围的函数表达式：

（2）

根据拟合函数

（2），画出胸围与体重关系的拟合图：

利用拟合函数及实际数据，求出实际值与拟合值得相对误差表：

表二、鲈鱼体重实际值与估计值对比及误差表

拟合值（cm）

462.1

489.7

609.3

784.1

1069.3

1428.1

4.13

1.60

7.86

6.55

6.39

2.50

7.98

2.81

从鲈鱼胸围与体重的拟合图，及表二中的数据，我们可以得出用线性函数拟合胸围与体重的关系拟合程度高，鲈鱼体重的实际值与估计值的相对误差不大，说明用线性函数拟合鲈鱼身长与体重的关系式可行的。

（三）、建立体重与身长、胸围相互影响的模型

实际情况下，鲈鱼的体重不可能只由身长、胸围单方面影响，因此考虑建立身长、胸围共同作用体重的模型。

此模型的建立是基于假设⑶，（4），即：

鲈鱼的体态用与胸围等周长，与身长等高的圆柱形来近似。

因为圆柱体的体积等于底面积乘高，底面积可以用周长表示：

.因此可以分析得出

.又物体质量等于密度与体积的乘积，因此只需根据数据求出密度即可。

于是身长、胸围与体重的关系可以表示为：

，问题转化为对系数

的求解。

根据已知数据，利用MATLAB软件求解，得到：

0.0327（3）

因此，

（4）

利用得出的函数对鱼的体重进行估测并列如下表：

表三、重量估计值及相对误差

估算值（g）

740

472

1115

490

1491

616

3.25

2.12

4.05

0.42

7.37

5.58

7.87

根据表三的数据，可以知道模型三的拟合程度也较好，相对于模型一、二，此模型充分考虑到了身长、胸围对体重的相互影响，用此模型估计鲈鱼的体重可能会更符合实际。