《运筹学》习题集Word格式文档下载.docx

《运筹学》习题集Word格式文档下载.docx

《《运筹学》习题集Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《《运筹学》习题集Word格式文档下载.docx（27页珍藏版）》请在冰豆网上搜索。

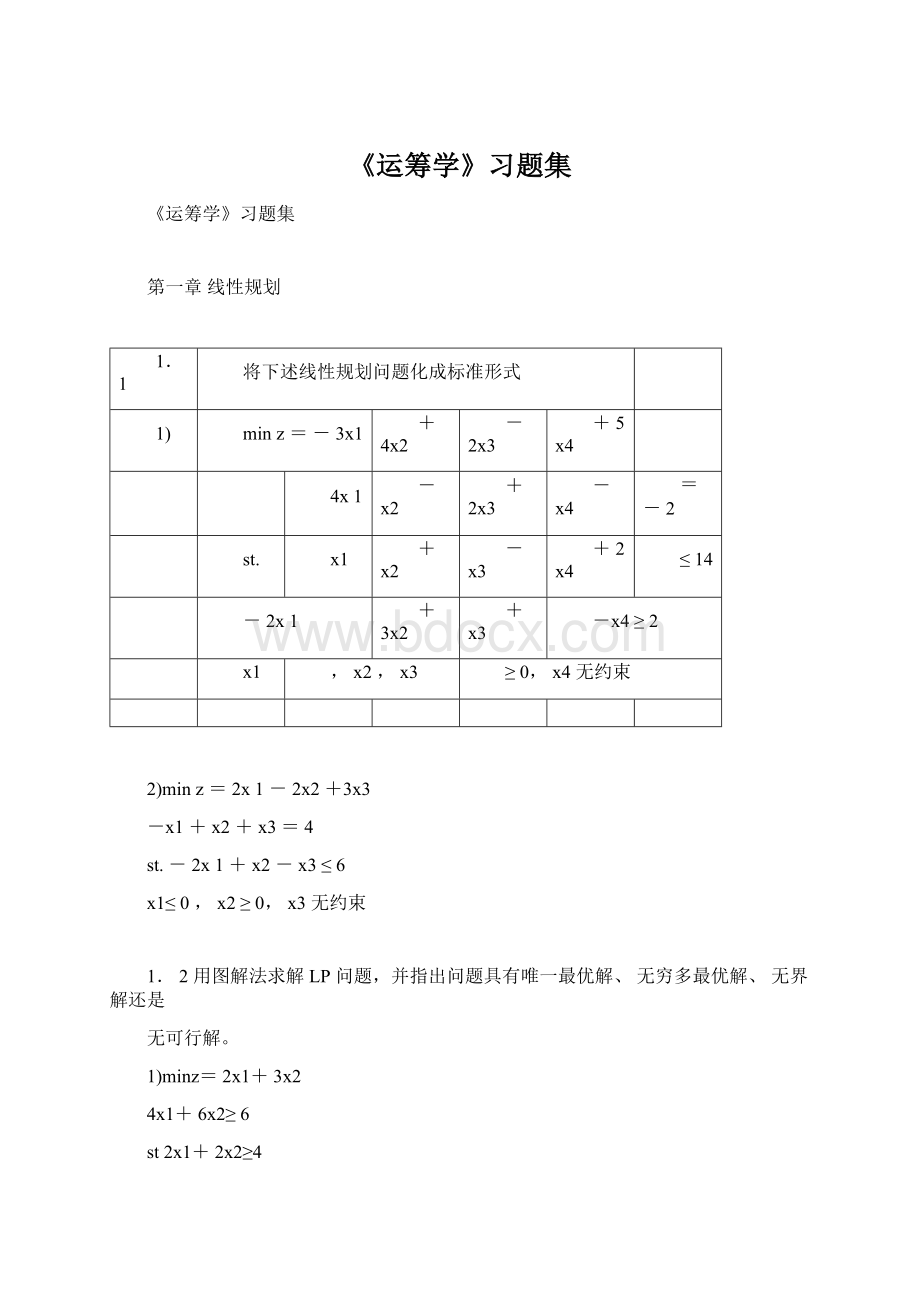
＋x

3

＋2x＝3

2

4

x1，x2，x3，x4≥0

1．4分别用图解法与单纯形法求解下列LP问题，并对照指出最优解所对应的顶点。

1）maxz＝10x1＋5x2

3x1＋4x2≤9

st5x1＋2x2≤8

2）maxz＝2x1＋x2

3x1＋5x2≤15

st6x1＋2x2≤24

1．5分别用大M法与两阶段法求解下列LP问题。

1）minz＝2x1＋3x2＋x3

x1＋4x2＋2x3≥8

st3x1＋2x2≥6

x1，x2，x3≥0

2）maxz＝4x1＋5x2＋x3

.3x1＋2x2＋x3≥18

St.2x1＋x2≤4

x1＋x2－x3＝5

3）maxz＝5x1＋3x2+6x3

x＋2x

－x≤18

2x1＋x2

－3x3≤16

x1＋x2

－x3＝10

x，x

，x≥0

4）maxz

10x1

15x2

12x3

5x1

3x2

x3

9

6x2

15x3

15

x2

2x1

5

x1,x2,x3

1．6

求下表中

～

l

的值。

a

c

（a）

－1

j

C

B

X

b

x

x4

6

（b）

（c）

（d）

x5

-1

（e）

（f）

［（g）］

1/2

（h）

（I）

-7

（j）

（k）

（l）

1.7某班有男生30人，女生20人，周日去植树。

根据经验，一天男生平均每人挖坑20个，

或栽树30棵，或给25棵树浇水；

女生平均每人挖坑10个，或栽树20棵，或给15棵树浇

水。

问应怎样安排，才能使植树（包括挖坑、栽树、浇水）最多？

请建立此问题的线性规划模型，不必求解。

1.8某糖果厂用原料A、B、C加工成三种不同牌号的糖果甲、乙、丙。

已知各种牌号糖果

中A、B、C含量，原料成本，各种原料的每月限制用量，三种牌号糖果的单位加工费及售价如下表所示。

问该厂每月应生产这三种牌号糖果各多少千克，使该厂获利最大？

试建立此问题的线性规划的数学模型。

甲

乙

丙

原料成本（元/千克）

每月限量（千克）

A

≥60％≥15％

2.00

2000

1.50

2500

≤20％≤60％≤50％

1.00

1200

加工费（元/千克）0.50

0.40

0.30

售

价

3.40

2.85

2.25

1.9某商店制定

7－12月进货售货计划，已知商店仓库容量不得超过

500件，6月底已存货

200件，以后每月初进货一次，假设各月份此商品买进售出单价如下表所示，问各月进货售货各多少，才能使总收入最多？

请建立此问题的线性规划模型。

月份

7

8

10

11

12

买进单价

28

24

25

27

23

售出单价

29

26

22

1.10某厂接到生产

A、B两种产品的合同，产品

A需200件，产品

B需300件。

这两种产

品的生产都经过毛坯制造与机械加工两个工艺阶段。

在毛坯制造阶段，产品

A每件需要2

小时，产品

B每件需要

4小时。

机械加工阶段又分粗加工和精加工两道工序，每件产品

需粗加工4

小时，精加工

10小时；

每件产品

B需粗加工

7小时，精加工12小时。

若毛坯

生产阶段能力为1700小时，粗加工设备拥有能力为

1000小时，精加工设备拥有能力为

3000

小时。

又加工费用在毛坯、粗加工、精加工时分别为每小时

3元、3元、2元。

此外在粗加

工阶段允许设备可进行

500

小时的加班生产，但加班生产时间内每小时增加额外成本

4.,5

元。

试根据以上资料，为该厂制订一个成本最低的生产计划。

1.11某公司有三项工作需分别招收技工和力工来完成。

第一项工作可由一个技工单独完成，

或由一个技工和两个力工组成的小组来完成。

第二项工作可由一个技工或一个力工单独去完

成。

第三项工作可由五个力工组成的小组完成，

或由一个技工领着三个力工来完成。

已知技

工和力工每周工资分别为

100元和80元，他们每周都工作

48小时，但他们每人实际的有效

工作小时数分别为

42和36。

为完成这三项工作任务，

该公司需要每周总有效工作小时数为：

第一项工作10000

第二项工作20000

小时，第三项工作30000

又能招收到的工

人数为技工不超过

400人，力工不超过800人。

试建立数学模型，确定招收技工和力工各多

少人。

使总的工资支出为最少

（

第二章对偶与灵敏度分析

2．1写出以下线性规划问题的DLP

1）minz＝2x1＋2x2＋4x3

x1＋3x2＋4x3≥2

2x1＋x2＋3x3

≤3

x＋4x＋3x

＝5

x1，x2≥0，x3无约束

2）maxz＝5x1＋6x2＋3x3

x1＋2x2＋2x3＝5

st－x1＋5x2－x3≥34x1＋7x2＋3x3≤8

x1无约束，x2≥0，x3≤0

3）maxz＝c1x1＋c2x2＋c3x3

a11x1＋a12x2＋a13x3≤b1

sta21x1＋a22x2＋a23x3＝b2

a31x1＋a32x2＋a33x3≥b3

x1≥0，x2≤0，x3无约束

2．2

对于给出的LP：

minz＝2x1＋3x2＋5x3＋6x4

x＋2x＋3x

＋x

≥2

－2x1＋x2－x3＋3x4

≤－3

xj≥0

（j=1,2,3,4

）

1）写出DLP；

2）用图解法求解DLP；

3）利用2）的结果及根据对偶性质写出原问题的最优解。

2．3

对于给出LP：

maxz＝x1＋2x2＋x3

x1＋

－

≤2

x1－x2＋

＝1

2x＋

x＋

x1≥0，x2

≤0，x3无约束

1）写出DLP；

2）利用对偶问题性质证明原问题目标函数值Z≤1

2．4

已知LP：

maxz＝x1＋x2

－x1＋x2＋x3

－2x1＋x2－x3

≤1

试根据对偶问题性质证明上述线性问题目标函数值无界。

2．5

给出LP：

maxz＝2x＋4x

x1＋3x2

＋x4≤8

2x1＋

≤6

x2＋

x3＋x4≤6

＋

x3≤9

2）已知原问题最优解X＝（2,2，4,0），试根据对偶理论，直接求出对偶问题的最优解。

2．6用对偶单纯形法求解下列线性规划问题

1）minz＝4x1＋12x2＋18x3

＋3x3

≥3

2x2＋2x3

≥5

xj≥0（j=1,2,3）

2）minz

2x2

4x3

3x1

2x3

st.6x1

5x3

2．7考虑如下线性规划问题

minz＝60x1＋40x2＋80x3

3x1＋2x2＋x3≥2

st4x1＋x2＋3x3≥4

2x1＋2x2＋2x3≥3

2）用对偶单纯形法求解原问题；

3）用单纯形法求解其对偶问题；

4）对比以上两题计算结果。

2．8已知LP：

maxz＝2x1－x2＋x3

x＋x

st－x＋2x

≤4

1）用单纯形法求最优解

2）

分析当目标函数变为

maxz＝2x

＋3x

时最优解的变化；

3）

分析第一个约束条件右端系数变为

时最优解的变化。

2．9给出线性规划问题

maxz＝2x1＋3x2＋x3

1/3x＋1/3x

＋1/3x≤1

1/3x＋4/3x

＋7/3x≤3

xj≥0

用单纯形法求解得最终单纯形表如下

－1

－3

－5

试分析下列各种条件下，最优解（基）的变化：

1）目标函数中变量x3的系数变为6；

2）分别确定目标函数中变量x1和x2的系数C1、C2在什么范围内变动时最优解不变；

3）约束条件的右端由

变为

；

2.10某厂生产甲、乙两种产品，需要

A、B两种原料，生产消耗等参数如下表（表中的消

耗系数为千克/件）。

产品原料

可用量（千克）

原料成本（元/千克）

160

1.0

180

2.0

销售价（元）

13

16

（1）请构造数学模型使该厂利润最大，并求解。

（2）原料A、B的影子价格各为多少。

（3）现有新产品丙，每件消耗3千克原料A和4千克原料B，问该产品的销售价格至少为多少时才值得投产。

（4）工厂可在市场上买到原料A。

工厂是否应该购买该原料以扩大生产？

在保持原问题最优基的不变的情况下，最多应购入多少？

可增加多少利润？

3.5某玩具公司分别生产三种新型玩具，每月可供量分别为1000、2000、2000件，它

们分别被送到甲、乙、丙三个百货商店销售。

已知每月百货商店各类玩具预期销售量均为

1500件，由于经营方面原因，各商店销售不同玩具的盈利额不同,见下表。

又知丙百货商店要求至少供应C玩具1000件，而拒绝进A玩具。

求满足上述条件下使总盈利额最大的供销分配方案。

可供量

1000

第三章运输问题

3．1

根据下表，用表上作业法求最优解。

B1

B2

B3

B4

产量

A1

A2

A3

销量

20

3．2

3．3

求给出的产销不平衡问题的最优解

3.4某市有三个面粉厂，他们供给三个面食加工厂所需的面粉，各面粉厂的产量、各面食加

工厂加工面粉的能力、各面食加工厂和各面粉厂之间的单位运价，

均式于下表。

假定在第

1，

2和3面食加工厂制作单位面粉食品的利润分别为

12元、16元和11元，试确定使总效益最

大的面粉分配计划（假定面粉厂和面食加工厂都属于同一个主管单位）

。

食品厂

面粉厂产值

面粉厂

30

3.5

光明仪器厂生产电脑绣花机是以产定销的。

已知

1至6月份各月的生产能力、合同销量

和单台电脑绣花机平均生产费用见下表：

正常生产能力（台）

加班生产能力（台）

销量（台）

单台费用（万元）

月份

60

104

50

75

14

90

115

13.5

100

40

103

80

70

已知上年末库存

103台绣花机，如果当月生产出来的机器当月不交货，

则需要运到分厂库房，

每台增加运输成本

0.1万元,每台机器每月的平均仓储费、

维护费为

0.2万元。

在7--8

月份销

售淡季，全厂停产

1个月，因此在

6月份完成销售合同后还要留出库存

80台。

加班生产机

器每台增加成本1

万元。

问应如何安排

1--6月份的生产，可使总的生产费用（包括运输、

仓储、维护）最少？

3.6设有A、B、C三个化肥厂供应

1、2、3、4四个地区的农用化肥。

假设效果相同，有关

数据如下表：

17

19

---

最低需要量

最高需要量

不限

试求总费用为最低的化肥调拨方案

第四章动态规划

4．1现有天然气站A，需铺设管理到用气单位E，可以选择的设计路线如下图，B、C、D

各点是中间加压站，各线路的费用如图所标注（单位：

万元），试设计费用最低的线路。

C1

D1

B2

C2

E

D2

B3

C3

4．2一艘货轮在A港装货后驶往

F港，中途需靠港加油、加淡水三次，从

A港到F港

全部可能的航运路线及两港之间距离如图，

F港有3个码头F1

，F

2，F3，试求最合

理停靠的码头及航线，使总路程最短。

F1

F2

F

45

F3

4．3某公司有资金

4万元，可向A、B、C三个项目投资，已知各项目的投资回报如下，

求最大回报。

项目

投资额及收益

41

48

66

42

64

68

78

76

4.4某厂有1000

台机器，高负荷生产，产品年产量S1与投入机器数Y1

的关系为S1＝8Y1，

机器完好率为

0.7；

低负荷生产，产品年产量

S2与投入机器数

Y2的关系为S2＝5Y2，机器

完好率为

0.9；

请制定一个五年计划，使总产量最大。

4.5某厂准备连续

3个月生产A种产品，每月初开始生产。

A的生产成本费用为x2，其中x

是A产品当月的生产数量。

仓库存货成本费是每月每单位为

1元。

估计

3个月的需求量分

别为d1＝

，2＝，3＝

120。

现设开始时第一个月月初存货

＝0，第三个月的月末存

d

110d

s