实验数据处理的基本方法Word格式.docx

实验数据处理的基本方法Word格式.docx

《实验数据处理的基本方法Word格式.docx》由会员分享，可在线阅读，更多相关《实验数据处理的基本方法Word格式.docx（9页珍藏版）》请在冰豆网上搜索。

从图线上还可以简便求出

实验需要的某些结果（如直线的斜率和截距值等），读出没有进行观测的对应点（内插法），或在一定条件下从图线的延伸部分读到测量范围以外的对应点

（外推法）。

此外，还可以把某些复杂的函数关系，通过一定的变换用直线图

表示出来。

例如半导体热敏电阻的电阻与温度关系为，取对数后得

到，若用半对数坐标纸，以lgR为纵轴，以1/T为横

轴画图，则为一条直线。

要特别注意的是，实验作图不是示意图，而是用图来表达实验中得到的物理量间的关系，同

时还要反映出测量的准确程度，所以必须满足一定的作图要求。

1）作图要求

（1）作图必须用坐标纸。

按需要可以选用毫米方格纸、半对数坐标纸、对数坐标纸或极坐标纸等。

（2）选坐标轴。

以横轴代表自变量，纵轴代表因变量，在轴的中部注明物理量的名称符号及其单位，单位加括号。

（3）确定坐标分度。

坐标分度要保证图上观测点的坐标读数的有效数字

位数与实验数据的有效数字位数相同。

例如，对于直接测量的物理量，轴上最小格的标度可与测量仪器的最小刻度相同。

两轴的交点不一定从零开始，一般

可取比数据最小值再小一些的整数开始标值，要尽量使图线占据图纸的大部分，不偏于一角或一边。

对每个坐标轴，在相隔一定距离下用整齐的数字注明分度

（参阅图1.7—1）。

（4）描点和连曲线。

根据实验数据用削尖的硬铅笔在图上描点，点子可不确定度大小相当。

点子要清晰，不能用图线盖过点子。

连线时要纵观所有据点的变化趋势，用曲线板连出光滑而细的曲线（如系直线可用直尺），连线不能通过的偏差较大的那些观测点，应均匀地分布于图线的两侧。

（5）写图名和图注。

在图纸的上部空旷处写出图名和实验条件等。

此外，还有一种校正图线，例如用准确度级别高的电表校准低级别的电表。

这种图要附在被校正的仪表上作为示值的修正。

作校正图除连线方法与上述作图要求不同外，其余均同。

校正图的相邻数据点间用直线连接，全图成为不光滑的折线（见图1.7—1）。

这是因为不知两个校正点之间的变化关系而用线性插入

法作的近似处理。

直流毫安计核准曲线表观值/（mA）

图1.7—1校准曲线图示例

2）作图举例

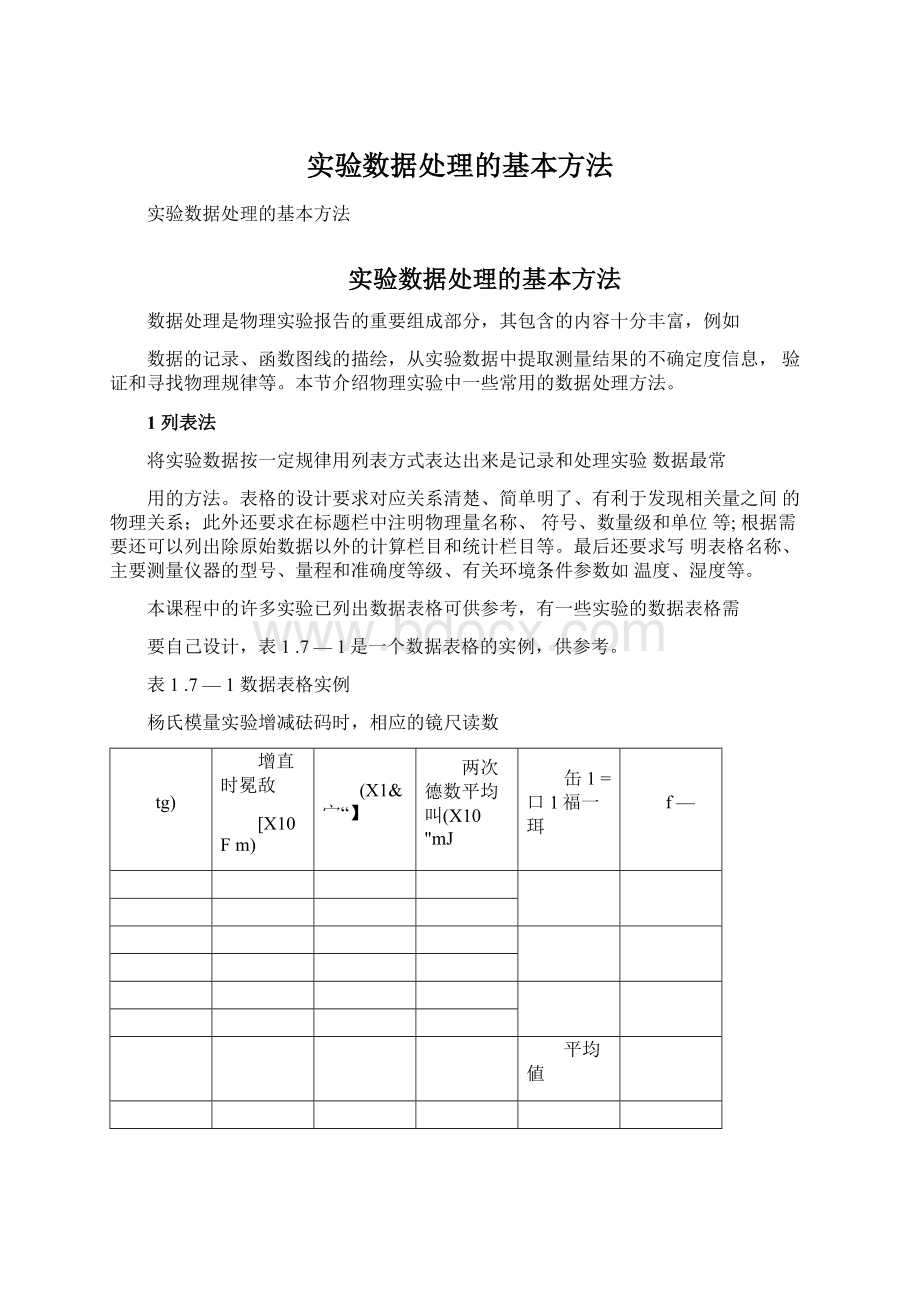
表1.7—2所列数据是测量约利秤弹簧伸长与受力的关系。

测量弹簧长度使用带有0.1mm游标的米尺。

加外力使用的是5个200mg的4级砝码，其误差限很小，对测量结果的不确定度的影响可以忽略。

表1.7—2弹簧伸长与受力关系数据表

if■码匝量

匿re負

平如位負L

tig）

fnni、

fnm）

E8.2

6L2

69,7

2D0

72,8

T5.2

74,0

400

B7.2

8?

.4

8E.3

6QD

1C1O

103.8

102.4

SOD

115.7

in.1

116.4

1COO

129,1

12^A

129.

作图示例见图1.7—2

图1.7—2作图示例

如果所作图线是一条直线，可以按以下方法求直线的斜率和截距。

直线方程为y=ax+b

在所作直线上选取相距较远的两点P、P2,从坐标轴上读取其坐标值P（X,Y）和P2（X,Y）代入式（1.7—1），可求得斜率a。

P、P2两点一般不取

原来测量的数据点。

为了便于计算，X、X两数值可选取整数。

在图上标出选取的P、P2点及其坐标。

斜率的有效数字位数要按有效数字运算规则确定。

图1.7—1例中劲度系数

截距b为x=0时的y值，可直接用图线求出。

但有的图线x轴的原点不在图上，用延长图线的办法，如果延得太长，稍有偏斜会导致b有很大误差。

这时，可采取从图线上再找一点P（X3，丫3），利用关系式

求得截距b。

用作图法表述物理量间的函数关系直观、简便，这是它的最大优点。

但是

利用图线确定函数关系中的参数（如直线的斜率和截距）仅仅是一种粗略的数据处理方法。

这是由于：

①作图法受图纸大小的限制，一般只能有3、4位有

效数字；

②图纸本身的分格准确程度不高；

③在图纸上连线时有相当大的主观任意性。

因而用作图法求取的参数，不可避免地会在测量不确定度基础上增加数据处理过程引起的不确定度。

一般情况下，用作图法求取的参数，只用有效数字粗略地表达其准确度就可以了。

如果需要确定参数测量结果的不确定度，最好采用直接由数据点去计算的方法（如最小二乘法等）求得。

3）曲线改直

按物理量的关系作出曲线虽然直观，但是作图和从图线中获得有关参数却比较困难。

许多函数形式可以经过适当变换成为线性关系，即把曲线改成直线，这样既便于作图，也便于求得有关参数。

举例如下。

（1）y=axb,a、b为常数，贝UIgy=Iga+bIgx,则lgy〜Igx直线的斜率为b,截距为Iga。

（2）y=aebx,a、b为常数，贝UIgy=Iga—bx/2.30,Igy〜x直线的斜率为—b/2.30,截距为Iga。

（3）y=ab,a、b为常数，贝UIgy=Iga+（Igb）x,Igy〜x直线的斜率为Igb,截距为Iga。

（4）y2=2px,p为常数，改变后，y=±

“2px，则y为a/x的线

性函数。

（5）1/y=a/x+b,a、b为常数，则1/y〜1/x直线的斜率为

a,截距为b。

4）用对数坐标纸作图

在某些情况下，变量变化范围很大，或者两物理量之间的关系为指数函数

或幕函数时，利用对数坐标纸作图往往更为方便。

对数坐标纸的分度与所表示量的对数值成正比，其每一循环（1,2,3,…，9,1）对应于一个数量

级，简称级。

用对数坐标纸作图时，可根据数据的覆盖范围选取不同的级。

全对数坐标纸两个坐标轴都以对数间距分度；

半对数坐标纸仅一个坐标以对数间距分度，而另一坐标仍以毫米均匀分度。

曲线改直例

（1）可用全对数坐标纸作图。

如用实验研究弹簧振子周期T

a

与振子质量m的关系。

令T=Am,人和a待定，测得振子质量m与振动周期T的数据后，就可以用全对数坐标纸作图，还可从图中确定A与a的值。

图1.7—2是在半对数坐标纸上作的半导体热敏电阻的R〜1/T关系图（半

导体热敏电阻电阻值随温度变化数据见表1.7—3）。

因该元件的电阻温度关系为，在普通坐标纸作图将是一条指数曲线，而在半对数纸上作

图即为一条直线。

图1.7—3半对数坐标纸作图示例

表1.7—3半导体热敏电阻电阻值随温度变化数据

t〔叩

8.10

20.80

29.DO

39.40

5L?

60.30

59.20

82.50

9LOO

99JO

T

27535

28L25

29B.Q5

303.OS

31L55

324.35

333.45

355血

3&

4.15

372.85

1

（X10■■I円

3,555

1402

3.300

3-210

3XS3

2.92L

2J12

274&

2$監

1604

1333

93L0

W.5

59BJ

煽4

364J

300.3

232J

2047

曲3

3最小二乘法

用作图法处理实验数据获得直线的斜率和截距等重要参数虽然简单明了，

但是存在相当大的主观成分，结果也往往因人而异。

最小二乘法则是一种比较精确的直线拟合方法。

它的依据是：

对于等精度测量若存在一条最佳拟合直线,那么各测量值与这条直线上的对应点值之差的平方和应为极小。

这里只考虑最简单的直线拟合问题。

假定每个数据点的测量都是等精度的，而且x的测量误差很小，可忽略，只有y的测量存在测量误差。

已知所观测的一组数据点（x,y「）（i=l,2,…，n），变量x与y有y=ax+b，并且x的测量误差远小于y的测量误差。

根据最小二乘原理估计a和b的值，应满足测量值y和直线上的对应点值（ax+b）之差的平方和为最小，即

（1.7—

-3）

确疋a，b使式

（1.7—3）

成立的必要条件是：

对a和b的一阶偏导

数等于零，即

（1.7

—4）

于是有

（1.7-

—5）

整理后写成

（1.7—6）

式中：

联合求解，得

（1.7—7）

要使式（1.7—3）取极小值还需满足充分条件，即其二阶导数大于零,这里不再证明。

衡量数据点在拟合直线两侧的离散程度，仍用标准偏差表示：

（1.7—8）

Sy表示以拟合直线y=ax+b求得的y值的标准不确定度的A类分量值。

根

据不确定度传递关系，可求得斜率a和截距b的标准不确定度A类分量：

必须指出，任何一组观测值（x,yO都可以通过式（1.7—7）得到系数a、b，也就是说x和y之间存在线性函数关系是预先设定好的，因此这种关系是否可靠需要验证。

可以通过相关系数丫来描述两个变量x、y的线性关系的明显程度。

（1.7—9）

丫是绝对值W1的数，丨丫丨越大，说明两个变量的线性关系越明显。

若丨丫|~1，说明Xi与y「间线性相关强烈；

|丫|~0，说明实验数据点分散，Xi与

y「无线性关系；

丫＞0（或丫＜0）表示y随x增加而增加（或y随x增加而减小）。

4逐差法

对于自变量等间距变化的数据组，常采用逐差法处理一元线性拟合问题。

逐差法与作图法相比，它不像作图法拟合直线具有较大的随意性，比最小二乘法计算简单而结果相近，在物理实验中是常用的数据处理方法。

设实验数据组

（x,yi）具有线性关系

y=ax+b

*按等间距变化，并且其测量误差远小于y的测量误差。

为了进行逐差法拟合直线，把数据分成两组:

进行等间隔逐差（隔n项）：

再利用y=ax+b的关系求得一组斜率值:

ai—（y“+i—y，）/（x”*一Xi）

a“=（y”一y”）/（x?

。

一x”）

取平均值

（1.7—10）

因为自变量Xi等间距变化，且其测量误差可以忽略，则有

（1.7—11）

x为自变量的变化间距；

n为逐差间隔数，即为测量次数的1/2。

a的A类不确定度分量

（1.7—12）

由此可见，逐差法处理数据是利用等间隔的数据点连了n条直线，分别求出每条直线的斜率后，再取平均值，得到拟合直线的斜率。

简单而言：

逐差法就是当一组数据比较多，如果要求每两个数据之间的平均间距的时候，如果直接用每相邻两数相减再求和取平均，那么中间的数据对于整个平均结果的影响就看不出来（中间的数据全部被抵消，剩下头尾两数相减）,这时候采用逐差法。

简单地举个例子，比如1,2,3,4,5,6,7,8,9,10,十个数，如果测量的结果由于误差不是恰好等于整数，比如等于

1.1,2.1,2.9,3.4,4.05,等等,这时把1-5和

6-10分别写在两排，上下对应，即

1,2,3,4,5

6,7,8,9,10

用6减1,7减2,8减3,9减4,10减5,得到五个差值,取平均后再除以5（即除以两次5）,这时就把这十个数中的误差对数据的影响全部计入了.

逐差法的使用条件是必须有偶数个数据，因为要写成两组对应的形

式.