 《探索勾股定理》试题精练Word格式.docx
《探索勾股定理》试题精练Word格式.docx
- 文档编号:20344991
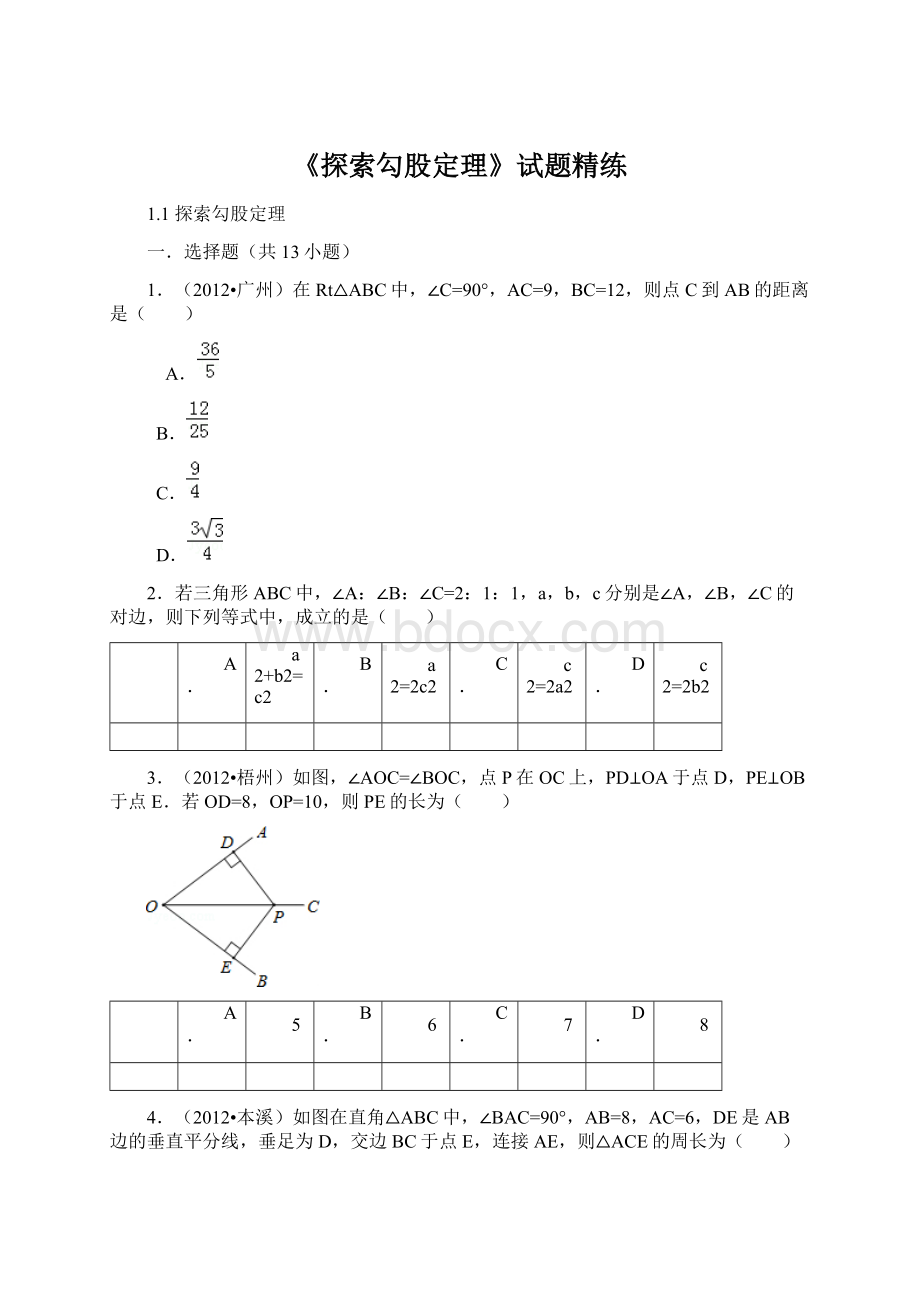
- 上传时间:2023-01-22
- 格式:DOCX
- 页数:25
- 大小:247.57KB
《探索勾股定理》试题精练Word格式.docx
《《探索勾股定理》试题精练Word格式.docx》由会员分享,可在线阅读,更多相关《《探索勾股定理》试题精练Word格式.docx(25页珍藏版)》请在冰豆网上搜索。
14
13
5.(2010•钦州)如图是一张直角三角形的纸片,两直角边AC=6cm、BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
4cm
5cm
6cm
10cm
6.(2009•衡阳)如图,矩形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,则AG的长为( )
1
2
7.(2009•滨州)已知△ABC中,AB=17,AC=10,BC边上的高AD=8,则边BC的长为( )
21
以上均不对
8.(2008•清远)如图,在Rt△ABC中,∠ACB=90°
,CD⊥AB于D,已知BC=8,AC=6,则斜边AB上的高是( )
10
9.如图,阴影部分是一个矩形,它的面积是( )
5cm2
3cm2
4cm2
6cm2
10.张大爷离家出门散步,他先向正东走了30m,接着又向正南走了40m,此时他离家的距离为( )
30m
40m
50m
70m
11.如图在△ABC中∠C=90°
,AD平分∠BAC交BC于D,若BC=64,且BD:
CD=9:
7,则点D到AB边的距离为( )
18
32
28
24
12.(2010•河池)如图所示,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用x,y表示直角三角形的两直角边(x>y),下列四个说法:
①x2+y2=49,②x﹣y=2,③2xy+4=49,④x+y=9.其中说法正确的是( )
①②
①②③
①②④
①②③④
13.(2003•山东)2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图),如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么(a+b)2的值为( )
19
25
169
二.填空题(共2小题)
14.(2009•长沙)如图,等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD= _________ cm.
15.(2006•安徽)如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是 _________ .
三.解答题(共3小题)
16.请选择一个图形来证明勾股定理.(可以自己选用其他图形进行证明)
17.下图甲是任意一个直角三角形ABC,它的两条直角边的边长分别为a、b,斜边长为c.如图乙、丙那样分别取四个与直角三角形ABC全等的三角形,放在边长为a+b的正方形内.
①图乙、图丙中
(1)
(2)(3)都是正方形.由图可知:
(1)是以 _________ 为边长的正方形,
(2)是以 _________ 为边长的正方形,(3)的四条边长都是 _________ ,且每个角都是直角,所以(3)是以 _________ 为边长的正方形.
②图中
(1)的面积 _________ ,
(2)的面积为 _________ ,(3)的面积为 _________ .
③图中
(1)
(2)面积之和为 _________ .
④图中
(1)
(2)的面积之和与正方形(3)的面积有什么关系?
为什么?
由此你能得到关于直角三角形三边长的关系吗?
18.(拓展创新)在教材中,我们通过数格子的方法发现了直角三角形的三边关系,利用完全相同的四个直角三角形采用拼图的方式验证了勾股定理的正确性.
问题1:
以直角三角形的三边为边向形外作等边三角形,探究S1+S2与S3的关系(如图1).
问题2:
以直角三角形的三边为斜边向形外作等腰直角三角形,探究S′+S″与S的关系(如图2).
问题3:
以直角三角形的三边为直径向形外作半圆,探究S1+S2与S3的关系(如图3).
参考答案
考点:
勾股定理;
点到直线的距离;
三角形的面积.
专题:
计算题.
分析:
根据题意画出相应的图形,如图所示,在直角三角形ABC中,由AC及BC的长,利用勾股定理求出AB的长,然后过C作CD垂直于AB,由直角三角形的面积可以由两直角边乘积的一半来求,也可以由斜边AB乘以斜边上的高CD除以2来求,两者相等,将AC,AB及BC的长代入求出CD的长,即为C到AB的距离.
解答:
解:
根据题意画出相应的图形,如图所示:
在Rt△ABC中,AC=9,BC=12,
根据勾股定理得:
AB=
=15,
过C作CD⊥AB,交AB于点D,
又S△ABC=
AC•BC=
AB•CD,
∴CD=
=
,
则点C到AB的距离是
.
故选A
点评:
此题考查了勾股定理,点到直线的距离,以及三角形面积的求法,熟练掌握勾股定理是解本题的关键.
等腰直角三角形;
三角形内角和定理;
勾股定理.
本题可根据三角形内角和180°
得出A、B、C三个角的大小.它们的比值即为边的比值,将三边代入三角形的勾股定理中,即可得出答案.
已知三角形ABC中,∠A:
1,并且三角的和是180度,因而可以求得:
∠A=90°
,∠B=∠C=45°
即这个三角形是等腰直角三角形,b=c,a是斜边.根据勾股定理得到:
a2=b2+c2=2c2.
故选B.
解决本题的关键是通过三角形的角的比值,求出角度,得到三角形是等腰直角三角形.
角平分线的性质;
由PD⊥OA,OD=8,OP=10,利用勾股定理,即可求得PD的长,然后由角平分线的性质,可得PE=PD.
∵PD⊥OA,
∴∠PDO=90°
∵OD=8,OP=10,
∴PD=
=6,
∵∠AOC=∠BOC,点P在OC上,PD⊥OA,PE⊥OB,
∴PE=PD=6.
此题考查了角平分线的性质与勾股定理.此题比较简单,注意角的平分线上的点到角的两边的距离相等.
线段垂直平分线的性质;
勾股定理.
首先连接AE,由在直角△ABC中,∠BAC=90°
,AB=8,AC=6,利用勾股定理即可求得BC的长,又由DE是AB边的垂直平分线,根据线段垂直平分线的性质,即可得AE=BE,继而可得△ACE的周长为:
BC+AC.
连接AE,
∵在Rt△ABC中,∠BAC=90°
,AB=8,AC=6,
∴BC=
=10,
∵DE是AB边的垂直平分线,
∴AE=BE,
∴△ACE的周长为:
AE+EC+AC=BE+CE+AC=BC+AC=10+6=16.
故选A.
此题考查了线段垂直平分线的性质与勾股定理.此题难度不大,注意掌握数形结合思想与转化思想的应用,注意垂直平分线上任意一点,到线段两端点的距离相等定理的应用.
翻折变换(折叠问题);
由勾股定理求得AB的长,由题意知BE是AB的一半.
∵两直角边AC=6cm、BC=8cm,
∴AB=
=10cm,
由题意知,点E是AB的中点,故BE=
AB=5cm.
本题考查图形的翻折变换,解题过程中应注意折叠是一种对称变换,它属于轴对称,对应边相等.
翻折变换(折叠问题).
根据折叠的性质和角平分线上的任意一点到角的两边距离相等计算.
由已知可得,△ADG≌△A′DG,BD=5
∴A′G=AG,A′D=AD=3,A′B=5﹣3=2,BG=4﹣A′G
在Rt△A′BG中,BG2=A′G2+A′B2可得,A′G=
则AG=
故选C.
本题主要考查折叠的性质,由已知能够注意到△ADG≌△A′DG是解决的关键.
以上答案都不对
分类讨论.
高线AD可能在三角形的内部也可能在三角形的外部,本题应分两种情况进行讨论.分别依据勾股定理即可求解.
在直角三角形ABD中,根据勾股定理,得BD=15;
在直角三角形ACD中,根据勾股定理,得CD=6.
当AD在三角形的内部时,BC=15+6=21;
当AD在三角形的外部时,BC=15﹣6=9.则BC的长是21或9.
故选D.
当涉及到有关高的题目时,注意由于高的位置可能在三角形的内部,也可能在三角形的外部,所以要注意考虑多种情况.
根据勾股定理求得AB的长,再根据三角形的面积公式求得CD即可.
∵BC=8,AC=6,
∴AB=10,
∵S△ABC=
×
6×
8=
10×
CD,
此题运用了直角三角形面积的不同表示方法及勾股定理的综合应用.
几何体的表面积;
勾股定理.
根据勾股定理先求出斜边的长度,再根据长方形的面积公式求出带阴影的矩形面积.
∵
=5厘米,
∴带阴影的矩形面积=5×
1=5平方厘米.
本题考查了勾股定理和长方形的面积公式.
正数和负数;
根据勾股定理直接求得斜边,即为他离家的距离.
=50m,
本题考查了正数和负数的意义以及勾股定理的运用,题目比较简单.
过D作DE⊥AB于E,根据角平分线的性质可以得到DE=CD,而根据已知条件可以求出CD的长,也就求出了DE的长.
如图,过D作DE⊥AB于E,
∵AD平分∠BAC交BC于D,而∠C=90°
∴CD=DE,
∵BC=64,且BD:
7,
∴CD=64×
=28,
∴DE=28,
则点D到AB边的距离为28.
此题主要利用角平分线的性质解题,把求则点D到AB的距离转化成求CD的长.
大正方形的面积是49,则其边长是7,显然,利用勾股定理可得①x2+y2=49;
小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即②x﹣y=2;
还可以得出四个三角形的面积+小正方形的面积=大正方形的面积,即4×
xy+4=49,化简得③2xy+4=49;
其中④x+y=
,故不成立.
①大正方形的面积是49,则其边长是7,显然,利用勾股定理可得x2+y2=49,故选项①正确;
②小正方形的面积是4,则其边长是2,根据图可发现y+2=x,即x﹣y=2,故选项②正确;
③根据图形可得四个三角形的面积+小正方形的面积=大正方形的面积,即4×
xy+4=49,化简得2xy+4=49,故选项③正确;
④
,则x+y=
,故此选项不正确.
本题利用了勾股定理、面积分割法等知识.
根据勾股定理,知两条直角边的平方等于斜边的平方,此题中斜边的平方即为大正方形的面积13,2ab即四个直角三角形的面积和,从而不难求得(a+b)2.
(a+b)2=a2+b2+2ab=大正方形的面积+四个直角三角形的面积和=13+(13﹣1)=25.
注意完全平方公式的展开:
(a+b)2=a2+b2+2ab,还要注意图形的面积和a,b之间的关系.
14.(2009•长沙)如图,等腰△ABC中,AB=AC,AD是底边上的高,若AB=5cm,BC=6cm,则AD= 4 cm.
先根据等腰三角形的性质求出BD的长,再根据勾股定理解答即可.
根据等腰三角形的三线合一可得:
BD=
BC=
6=3cm,在直角三角形ABD中,
由勾股定理得:
AB2=BD2+AD2,
所以,AD=
=4cm.
本题考查了等腰三角形的性质和勾股定理.关键要熟知等腰三角形的三线合一可得.
15.(2006•安徽)如图,直线L过正方形ABCD的顶点B,点A、C到直线L的距离分别是1和2,则正方形的边长是
.
直角三角形全等的判定.
两直角三角形的斜边是正方形的两边,相等;
有一直角对应相等;
再根据正方形的角为直角,可得到有一锐角对应相等,易得两直角三角形全等,由三角形全等的性质可把2,1,正方形的边长组合到直角三角形内得正方形边长为
如图,
∵四边形ABCD是正方形,
∴AB=CD,∠ABM+∠CBN=90°
而AM⊥MN,CN⊥BN,
∴∠BAM=∠CBN,∠AMB=∠CNB=90°
∴△AMB≌△BCN,
∴BM=CN,
∴AB为
本题考查勾股定理及三角形全等的性质应用.
勾股定理的证明.
证明题;
开放型.
选第一个图形证明,都来表示中间正方形的面积.有两种表示方法:
直接表示正方形的面积;
用大正方形的面积﹣4个全等的直角三角形的面积.
∵外部是四个全等的直角三角形,
∴中间的四边形为正方形
正方形的面积=c2,
正方形的面积=(a+b)2﹣4×
ab=a2+b2
∴a2+b2=c2
用构图法来解释勾股定理,通常情况下是运用不同的方式来表示面积得到的结果.
(1)是以 a 为边长的正方形,
(2)是以 b 为边长的正方形,(3)的四条边长都是 c ,且每个角都是直角,所以(3)是以 c 为边长的正方形.
②图中
(1)的面积 a2 ,
(2)的面积为 b2 ,(3)的面积为 c2 .
③图中
(1)
(2)面积之和为 a2+b2 .
根据图形可以直接得出各正方形的边长,进而得出各正方形面积,再通过两个组合正方形的面积之间相等的关系即可证明勾股定理.
(1)是以a为边长的正方形,
(2)是以b为边长的正方形,
(3)的四条边长都是c,且每个角都是直角,所以(3)是以c为边长的正方形.
②图中
(1)的面积a2,
(2)的面积为b2,(3)的面积为c2.
③图中
(1)
(2)面积之和为a2+b2.
④由图乙和图丙可知大正方形的边长为:
a+b,则面积为(a+b)2,图乙中把大正方形的面积分为了四部分,分别是:
边长为a的正方形,边长为b的正方形,还有两个长为b,宽为a的长方形,
根据面积相等得:
(a+b)2=a2+b2+4×
ab,
由图丙可得(a+b)2=c2+4×
ab.
所以a2+b2=c2.
故答案为:
①a,b,c,c;
②a2,b2,c2;
③a2+b2.
本题考查了利用图形面积的关系证明勾股定理,解题关键是利用三角形和正方形边长的关系进行组合图形,
探究型.
这三道题主要在勾股定理的基础上结合具体图形的面积公式,运用等式的性质即可得到相同的结论.
探究1:
由等边三角形的性质知:
S1=
a2,S2=
b2,S3=
c2,
则S1+S2=
(a2+b2),因为a2+b2=c2,所以S1+S2=S3.
探究2:
由等腰直角三角形的性质知:
S′=
a2,S″=
b2,S=
c2.
则S′+S″=
(a2+b2),因为a2+b2=c2,所以S′+S″=S.
探究3:
由圆的面积计算公式知:
πa2,S2=
πb2,S3=
πc2.
π(a2+b2),因此a2+b2=c2,所以S1+S2=S3.
熟悉各种图形的面积公式,结合勾股定理,运用等式的性质进行变形.
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 探索勾股定理 探索 勾股定理 试题 精练
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 如何打造酒店企业文化2刘田江doc.docx
如何打造酒店企业文化2刘田江doc.docx
