最新和倍问题精品讲义教师版Word格式.docx

最新和倍问题精品讲义教师版Word格式.docx

《最新和倍问题精品讲义教师版Word格式.docx》由会员分享，可在线阅读，更多相关《最新和倍问题精品讲义教师版Word格式.docx（18页珍藏版）》请在冰豆网上搜索。

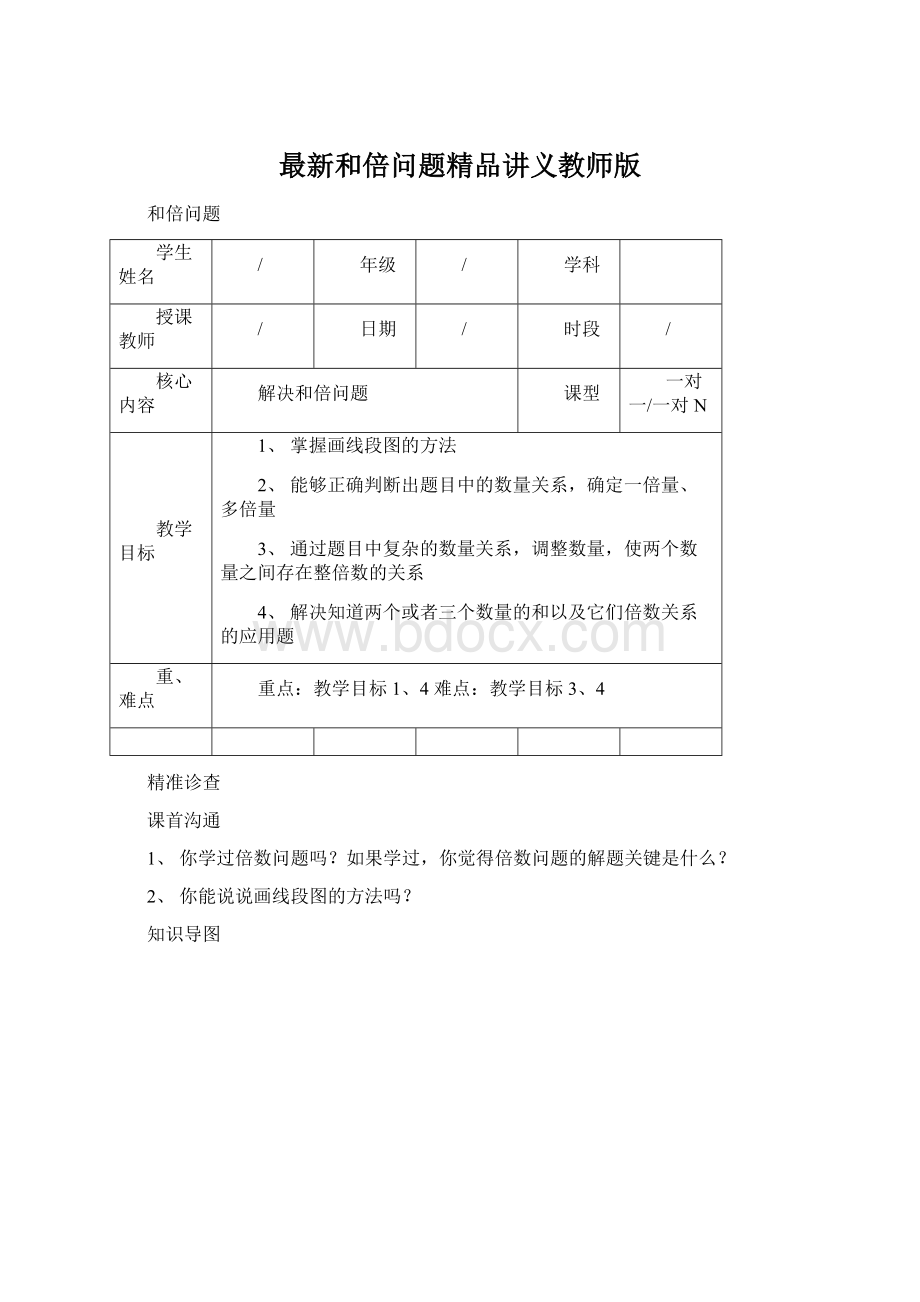
4×

4=16（只）

互动导学

导学一：

画线段图协助解决倍数问题

知识点讲解1：

画线段图的方法先确定一倍量，通常以1厘米或者2厘米长度表示一倍量，再找准多倍量，多少倍就用多少厘米表示。

例题

1、依照下列题目的数量关系画线段图：

甲是乙的2倍，乙是丙的三倍

常见思维障碍：

3个数量关系，无法准确找到一倍量，并且画的时候不懂从上往下是一倍量到多倍量。

先确定倍数关系：

一倍量是丙，多倍量分别是甲、乙；

乙是3倍量，甲是6倍量。

先画好甲丙1厘米长，乙画3厘米长，甲画6厘米长。

我爱展示

1、

2、甲比乙多3倍

3、甲是乙的2倍，丙是乙的3倍

导学二：

倍数关系明确的题型

常用的关系式

1、（2011年越秀区五年级数学《倍数的变换、因数与倍数》单元检测卷——应用题10）妈妈买了一套西装，共用去1350元，其中上衣的价钱是裤子的2倍。

裤子的价钱是多少元？

【参考答案】450元

【解析】1350÷

（2+1）=450（元）

答：

裤子的价钱是450元。

【思维对话】常见思维障碍：

不能准确判断一倍量是上衣还是裤子。

老师讲解时，建议让学生把几道题目都读一遍，找找几道应用题中相似的句子。

提问1：

你发现这几道应用题中，有什么相似的地方？

例如一些句子。

（引导学生发现倍数问题的应用题的共同点就是有相似的数量关系的句子：

“A和B的和是多少，A是B的几倍”）

提问2：

从这些句子里面，我们是可以发现两个数量存在的倍数关系的，我们可以从中确定谁是一倍量。

例如“上衣的价钱是裤子的2倍”，判断一倍量是上衣呢？

还是裤子呢？

（引导学生自己找到一倍量）

分析倍数关系的句子有固定模式：

“A是B的几倍”那么也就是应该理解为：

“多倍量是一倍量的几倍”。

【学有所获】发现多倍量和多倍量在题中位置的规律：

“是的几倍”

[学有所获答案]多倍量；

一倍量

2、小明和妈妈的年龄加在一起是45岁，妈妈的年龄是小明的4倍，小明和妈妈各是多少岁？

【参考答案】小明9岁；

妈妈36岁

【解析】

小明岁数：

妈妈岁数：

或

答：

小明今年9岁，妈妈今年36岁。

把小明的岁数作为一倍量，则妈妈的岁数为小明的4倍，那么小明和妈妈的岁数之和相当于小明岁数的5倍，用小明和妈妈岁数和除以5就是小明的岁数。

1、学校有科技书和故事书共480本，科技书的本数是故事书的3倍。

两种书各有多少本？

【参考答案】故事书：

120本；

科技书：

360本。

【解析】故事书的本数：

480÷

（3+1）=120（本）

科技数的本数：

120×

3=360（本）

故事书有120本，科技书有360本。

【思维对话】画线段图协助解题

把故事书的本数看作1份，也就是一倍量；

科技书是故事书的3倍，也就是3份。

两种书一共有4份，则把480平均分成4份。

其中1份就是故事书，再求出故事书的3份就是科技书的本数。

2、被除数与除数的和为320，商是7，被除数和除数各是多少？

【参考答案】除数40；

被除数280。

【解析】除数：

320÷

（7＋1）=40

被除数：

40×

7=280

3、小聪和小明共有60个玻璃球，小聪的玻璃球是小明的3倍，他们俩各有玻璃球多少个？

【参考答案】小明15个；

小聪45个。

【解析】小明玻璃球数：

60÷

（3+1）=15（个）

小聪玻璃球数：

15×

3=45（个）

小聪有45个玻璃球，小明有15个玻璃球。

导学三：

多个数量存在倍数关系的题型。

1、果园里有梨树、桃树和苹果树共1200棵，其中梨树的棵数是苹果树的3倍，桃树的棵数是苹果树的4倍。

求梨树、桃树和苹果树各有多少棵？

【参考答案】苹果树150棵，梨树450棵，桃树600棵。

【解析】苹果树有1200÷

（1+3+4）=150（棵）

梨树树有150×

3=450（棵）

桃树树有150×

4=600（棵）

苹果树有150棵，梨树有450棵，桃树有600棵。

（1）知道梨树和苹果树有倍数关系，也知道桃树和苹果树有倍数关系，不懂3者与和的关系。

障碍点突破方法：

找准数量关系，然后利用线段图，画出它们，再分析。

你能找到题目中以哪种果树作为一倍量吗？

（引导学生发现梨树和桃树都是以苹果树为一倍量）

都是苹果树为一倍量，那梨树和桃树分别是几倍量？

你能画线段图表示出来吗？

如果学生会画，则不需要再细讲画图方法，如果不会则再次讲。

提问3：

现在你发现三种果树一共是几倍量？

我们要如何求出一倍量，也就是求出我们的苹果树多少棵？

如果学生能够直接说出三种果树一共是8倍，也就是8份，再让他用前学过的公式解决问题。

如果学生不懂，则要通过线段图一份一份地数给他看，让他知道三种水果树一共8份，要把总棵树平均分成8份。

【学有所获】在一倍量相同的多倍量数量关系的题型中，找到几种数量各是多少倍，然后按照公式解决问题。

一倍量=和÷

（倍数A+倍数B+1）苹果树：

1200÷

（3+4+1）=150（棵）

多倍量A=一倍量×

倍数A梨树树：

150×

多倍量B=一倍量×

倍数B桃树树：

2、已知鸡、鸭、鹅共110只，鸭的只数是鸡的2倍，鹅的只数是鸭的4倍。

问鸡、鸭、鹅各多少只？

【参考答案】鸡10只，鸭20只，鹅80只。

鸡的只数：

鸭的只数：

鹅的只数：

鸡有10只，鸭有20只，鹅有80只。

（1）3种数量的倍数关系理不清。

（2）线段图不会画。

思维障碍点

（1）突破方法：

这道题哪些句子可以知道倍数关系的，你能够找出来吗？

（引导学生读题找倍数关系的句子，获取倍数关系信息。

）

这2句数量关系关键句里面的一倍量相同吗？

你能够说出是以哪种动物为一倍量吗？

（引导学生逐渐分析找好一倍量，前一句是“鸡”，后一句是“鸭”。

鸡和鸭都是一倍量，你觉得谁比较小？

如果让你选择其中一个为一倍量，你会怎么选择？

（引导学生发现鸡比较小，那么也就是我们的标准的一倍量，接着鸭是2倍量，最后鹅是鸭的4倍，也就是4个2倍量，就是8倍量。

思维障碍点

（2）突破方法：

题目的数量关系已经分析过了，现在我们画线段图，你可以告诉老师画哪种动物为一倍量吗？

那么以鸡为一倍量，鸭要怎么画？

那我们的鹅呢？

以谁为一倍量，画多少倍？

学生会有2种回答，一种是以鸡为一倍量，画8份；

另外一种是以鸭为一倍量，画4份。

但是要注意第二种是以鸭的长度为一份进行画图。

【学有所获】学会画线段图；

在复杂的倍数关系中找准一倍量解决问题。

1、B是A的2倍，C是A的3倍，B和C共50，求A是多少？

【参考答案】10.

【解析】50÷

（3+2）=10

A是10。

2、有三个书橱共放了330本书，第二个书橱里的书是第一个的2倍，第三个书橱里的书是第二个的4倍。

每个书橱里各放了多少本书？

【参考答案】第一：

30本；

第二：

60本；

第三：

240本

第一：

330÷

11=30（本）

30×

2=60（本）

60×

4=240（本）

第一个放了30本，第二个放了60本，第三个放了240本。

3、（2011年广州小联盟真题卷应用题5）把一条大鱼分成鱼头、鱼身和鱼尾三部分，鱼尾重5千克，鱼头的重量等于鱼身重量的一半，而鱼身的重量等于鱼头的重量加上三个鱼尾的重量，这条大鱼重多少千克？

【参考答案】50千克。

鱼头：

5×

3=15（千克）

鱼身：

2=30（千克）

大鱼：

5+15+30=50（千克）

这条大鱼50千克。

倍数关系不明确的题型

1、（2011年越秀区五年级数学《倍数的变换、因数与倍数》单元检测卷——选做题4）

长江全长6300千米，比珠江的3倍多300千米。

珠江全长有多少千米？

【参考答案】2000千米。

（6300－300）÷

3

=6000÷

=2000（千米）

2、少先队员种柳树和杨树共216棵，杨树的棵数比柳树的3倍多20棵，两种树各种了多少棵？

【参考答案】柳树49棵；

杨树167棵。

216－20=196（棵）

柳树：

196÷

（1＋3）=49（棵）

杨树：

216－49=167（棵）。

略。

常见思维障碍点

（1）看到不是整数倍，不知道如何处理多出来的20棵树。

这道题你可以在读完题目时获取到什么条件？

（引导学生关注题目给的信息）

如果杨树没有这多出来的20棵，你会不会解决？

（引导学生先处理多出来的20棵）

如果杨树少20棵，总数会发生什么变化？

杨树这时候是柳树的多少倍？

（引导学生用总数的“216－20”，使树的总棵树刚好是柳树的整数倍）

提问4：

如果题目变成“杨树的棵数比柳树的3倍少20棵”，那解决方法还是一样吗？

（把题目改变，诊查学生是否真正理解解决方法，也就是不管是比整数倍多一些，还是比整数倍少一些都会解决这些问题）

【学有所获】懂得通过加减法，使另外一个刚好是一倍量的整数倍，然后解决问题。

发现题目条件是比一倍量的几倍多若干，就用和减去这若干数量，使“和”变成一倍量的整数倍量；

如果题目条件是比一倍量的几倍少若干，就用和加上这若干数量，使“和”变成一倍量的整数倍量。

1、小华和小明两人参加数学竞赛，两人共得168分，小华的得分比小明的2倍少42分。

两人各得多少分？

【参考答案】小明70分；

小华98分。

（168＋42）÷

（2＋1）

=210÷

小明：

=70（分）

小华：

168-70=90分

略

2、学校购买了720本图书分给高、中、低三个年级，高年级分得的比低年级的3倍多8本，中年级分得的比低年级的2倍多4本。

高、中、低年级各分得图书多少本？

【参考答案】低年级：

118本；

中年级：

240本；

高年级：

362本。

【解析】（720－8－4）÷

（1＋3＋2）

=708÷

6

低年级：

=118（本）

中年级：

118×

2＋4=240（本）

高年级：

3＋8=362（本）

3、某汽车运输场有大小货车共115辆，大货车比小货车的5倍还多7辆，这个运输场有大小货车多少辆？

【参考答案】大货车97辆；

小货车18辆。

【解析】小货车：

（115-7）÷

（5+1）=18（辆）

大货车：

18×

5+7=97（辆）

导学四：

变化后形成倍数关系的题型

1、甲、乙两个粮库原来共存粮170吨，后来从甲库运出30吨，给乙库运进10吨，这时甲库存粮是乙库存粮的2倍，两个粮库原来各存粮多少吨？

【参考答案】甲库原有：

130吨；

乙库原有：

40吨。

【解析】后来甲、乙粮库存粮总和为：

170-30+10=150（吨）

乙库存粮为

甲库存粮为100-50=100（吨）或

原来甲库存粮：

100+30=130（吨）

原来乙库存粮：

50-10=40（吨）

甲库原来有存粮130吨，乙库原来有存粮40吨。

（1）被运来运去弄晕了，找不到最后2个仓库的总和是多少。

你能够算出最后2个仓库存粮多少吨吗？

（引导学生发现：

甲库运出30吨，乙库运进10吨，则此时甲、乙两个粮库的存粮总数变成170-30+10=150吨）。

你能够求出现在乙库存多少吨吗？

（引导学生解决问题：

这时甲库存粮是乙库存粮的2倍，这是总和是乙库的3倍，利用公式解决问题。

）

【学有所获】理解部分量增加或减少，总量也随着增加或者减少的原则。

2、学校饭堂买回大米和面粉共1000千克，面粉用去200千克，大米用去50千克，剩下的大米比剩下的面粉的2倍多30千克。

饭堂买回来大米和面粉各多少千克？

【参考答案】大米：

560千克；

面粉：

440千克。

剩下的面粉：

（1000－200－50－30）÷

（1＋2）=240（千克）

买回的大米：

240×

2＋30＋50=560（千克）

买回的面粉;

240＋200=440（千克）

【思维对话】常见思维障碍点：

（1）看到条件繁多，找不到和倍问题的模型。

（2）不懂处理条件中的用去的那些重量。

例如“面粉用去200千克，大米用去50千克”

这道题是和倍问题吗？

我们学过的和倍问题是如何的？

（引导学生进行思考，总结和倍问题的特征）

这道题跟我们前面学的问题有什么不同？

（引导学生进行分析，理清题目中的条件）

题目中那些数量形成倍数关系？

（引导学生把“剩下的数量形成倍数关系”，作为解题关键入口）

如果这道题只知道面粉和大米剩下的重量，你会解决吗？

（引导学生处理前面用去的那些面粉和大米，求出剩下的总重量：

1000－200－50=750千克）

那么现在剩下的大米、面粉之间的关系刚好是整数倍关系吗？

（引导学生处理倍数关系条件中多出的30千克的数量：

750-30=720千克）

那现在我们应该怎么去求出剩下的面粉重量呢？

（引导学生利用和倍问题的公式求出一倍量：

剩下的面粉720÷

（1+2）=240千克）

【学有所获】教学生逐步分析题目中的复杂的数量关系，让学生掌握把条件逐个解决然后求出问题，同时学会看到复杂题目中的题型的原形。

1、两箱茶叶共176千克，从甲箱取出30千克放乙箱，乙箱的千克数就是甲箱的3倍。

两箱原有茶叶多少千克？

【参考答案】甲箱原有茶叶74千克，乙箱原有茶叶102千克

【解析】甲箱取出30千克放乙箱后，和还是不变的。

甲箱有茶叶：

176÷

（3+1）=44（千克）

乙箱有茶叶：

176-44=132（千克）

所以，甲箱原有茶叶：

44+30=74（千克）

乙箱原有茶叶：

132-30=102（千克）

甲箱原有茶叶74千克，乙箱原有茶叶102千克。

2、甲油库原存油是乙油库的6倍，若两油库各增加30吨油后，甲库存量是乙库存量的3倍。

求两油库原存油量各多少吨？

【参考答案】乙库原有：

20吨；

甲库原有：

120吨。

【解析】乙库原有：

2÷

（5－2）=20（吨）

甲库原有：

20×

6=120（吨）

3、三个筑路队共筑路1360米，甲队筑的米数是乙队的2倍，乙队比丙队多240米。

三个队各筑多少米？

【参考答案】乙队筑：

400米；

甲队筑：

800米；

丙队筑：

160米。

【解析】把乙队的米数看作1份，甲队筑的米数是这样的2份。

假设丙队多筑240米，那么三个队共筑了1360＋240=1600米，正好是乙队的2＋1＋1=4倍。

所以，乙队筑了1600÷

4=400米，甲队筑了400×

2=800米，丙队筑了400－240=160米。

能力展示

限时考场模拟10分钟完成

1、哥哥和弟弟共有图书24本，哥哥的图书本数是弟弟的2倍，哥哥和弟弟各有多少本图书？

【参考答案】弟弟8本；

哥哥16本。

【解析】弟弟图书本数：

24÷

（2+1）=8（本）

哥哥图书本数：

8×

2=16（本）

2、弟弟有课外书20本，哥哥有课外书25本，哥哥给弟弟多少本后，弟弟的课外书是哥哥的2倍？

【参考答案】哥哥给弟弟10本。

【解析】哥哥、弟弟两人共有25+20=45（本）

弟弟的课外书是哥哥的2倍，根据公式

此时哥哥课外书本数是：

哥哥给弟弟课外书本数是：

哥哥给弟弟10本后，弟弟的课外书是哥哥的2倍。

3、姐姐有32元钱，弟弟有18元钱，弟弟给姐姐多少钱后，姐姐的钱比弟弟的钱多3倍？

5、你认为一件DIY手工艺制品在什么价位可以接受？

【参考答案】弟弟给姐姐8元。

随科技的迅速发展，人们的生活日益趋向便捷、快速，方便，对于我国传统的手工艺制作，也很少有人问津，因此，我组想借此创业机会，在校园内开个DIY创意小屋。

它包括编织、刺绣、串珠等，让我们传统的手工制作也能走进大学，丰富我们的生活。

【解析】姐姐和弟弟一共有钱：

32+18=50（元）

大学生个性化消费增多是一种趋势。

当前社会、经济飞速发展，各种新的消费品不断增多，流行文化时尚飞速变化，处于校园与社会两者之间的大学生肯定会受影响。

目前在大学校园，电脑、手机、CD、MP3、录音笔被称为大学生的“五件武器”。

除了实用，这也是一种表明自己生活优越的炫耀性的东西。

现下很大一部分大学生中的“负债消费”表现的典型的超前享乐和及时行乐——其消费项目多半是用于奢侈浪费的非必要生活消耗。

如举办生日宴会、打网球、保龄球、上舞厅跳舞、进夜总会唱“卡拉ＯＫ”等。

“负债消费”使很多学生耽于物欲，发展严重者轻则引起经济纠纷，动武斗殴，影响同窗友谊，重则引发犯罪事件，于社会治安不利。

弟弟给姐姐钱后，弟弟有：

50÷

（3+1+1）=10（元）

姐姐有：

50-10=40（元）

我们长期呆在校园里，对社会缺乏了解，在与生意合作伙伴应酬方面往往会遇上困难，更不用说商业上所需经历的一系列繁琐手续。

他们我们可能会在工商局、税务局等部门的手续中迷失方向。

对具体的市场开拓缺乏经验与相关的知识，缺乏从职业角度整合资源、实行管理的能力；

弟弟给姐姐的钱为：

18-10=8（元）

弟弟给姐姐8元后，姐姐的钱比弟弟的钱多3倍。

“碧芝”的成功归于他的唯一，这独一无二的物品就吸引了各种女性的眼光。

课后作业

300元以下918%1、秋收之后，红星农场把56000千克粮食分别存入两个仓库，已知往第一个仓库里存放的粮食是第二仓库的3倍，求两个仓库各存粮食多少千克？

（四）DIY手工艺品的“个性化”【题型】解答题

【参考答案】第一仓库42000千克第二14000千克。

【解析】第二仓库存粮食：

56000÷

（3+1）=14000（千克）

第一仓库存粮食：

56000-14000=42000（千克）

2、甲、乙两个冷藏库共存鸡蛋6350箱，乙库存的鸡蛋比甲库剩下的2倍还多350箱，求甲、乙两库各存鸡蛋多少箱？

（三）上海的文化对饰品市场的影响【题型】解答题

手工艺制品是我国一种传统文化的象征，它品种多样，方式新颖，制作简单，深受广大学生朋友的喜欢。

当今大学生的消费行为表现在追求新颖，追求时尚。

追求个性，表现自我的消费趋向：

购买行为有较强的感情色彩，比起男生热衷于的网络游戏，极限运动，手工艺制品更得女生的喜欢。

【参考答案】甲库存：

2000箱；

乙库存：

4350箱。

【解析】甲库存鸡蛋：

（6350-350）÷

（2+1）=2000（箱）

乙库存鸡蛋：

2000×

2+350=4350（箱）

甲库存鸡蛋2000箱，乙库存鸡蛋4350箱。

3、A地有工人170人，B地有工人100人，要使A地的工人是B地的工人人数的2倍，需从B地调多少人到A地？

（3）心态问题【题型】解答题

【参考答案】从B调80人。

【解析】A、B两地工人总和是：

170+100=270（人）

调人后A地人数：

270÷

（2+1）=90（人）

需要调人170-90=80（人）

要使A地的工人是B地的工人人数的2倍，需从B地调80人到A地。

4、甲、乙、丙三个修路队共修路1200米，甲队修的米数是乙队的2倍，乙队修的米数是丙队的3倍。

三个队各修了多少米？

【参考答案】甲：

720米；

乙队360米；

丙120米。

【解析】丙队修了：

（3+6+1）=120（米）

乙队修了：

3=360（米）

甲队修了：

360×

2=720（米）

跟踪指导

1、学完这节课的内容后，回去遇到一些数学问题，画线段图协助解题。

2、标注理解不够深刻的例题回去复习。

3、总结和倍问题的题型特征。