SPSS统计软件期末作业Word文档下载推荐.docx

SPSS统计软件期末作业Word文档下载推荐.docx

《SPSS统计软件期末作业Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《SPSS统计软件期末作业Word文档下载推荐.docx（22页珍藏版）》请在冰豆网上搜索。

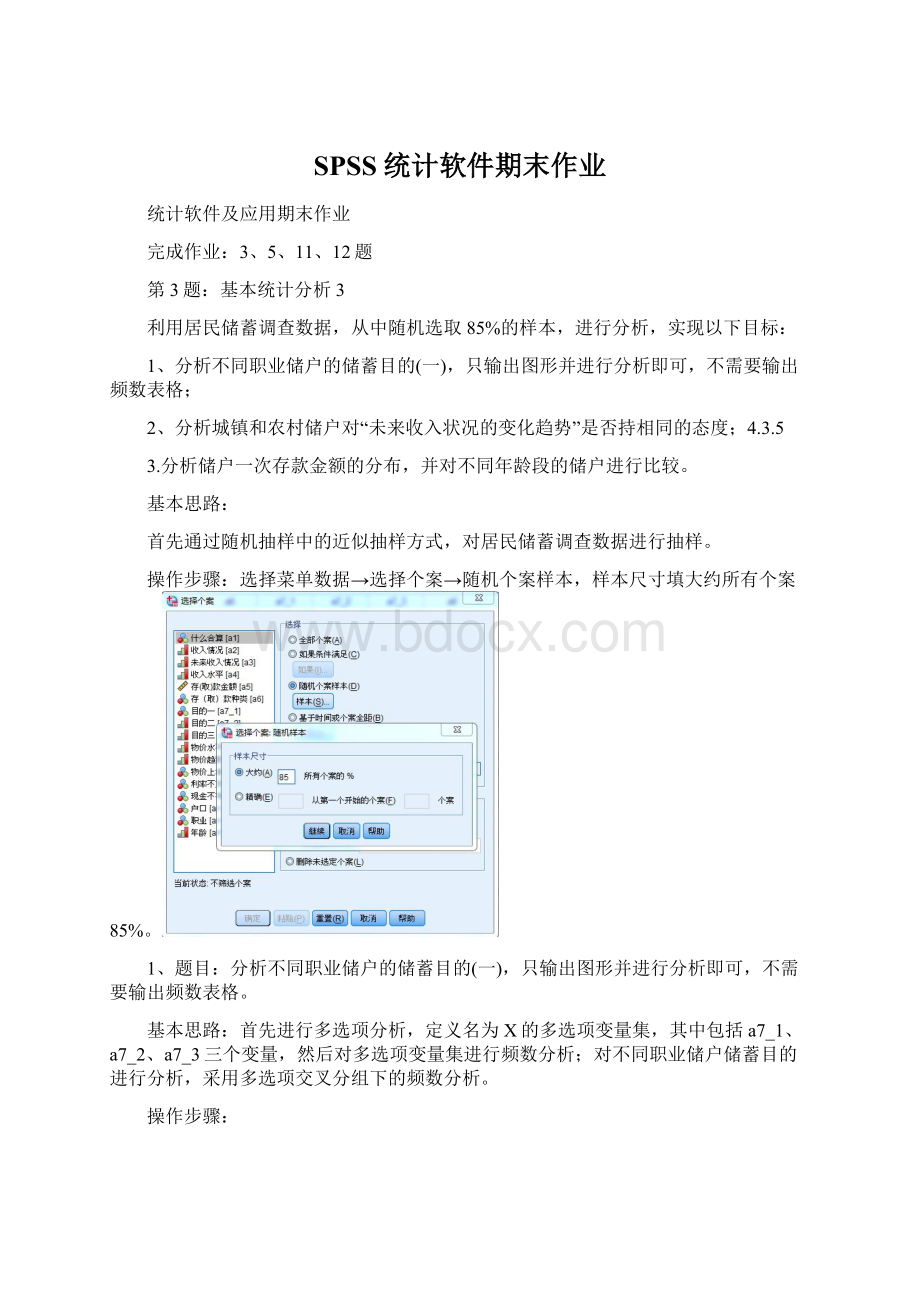
11.8%

100.0%

未来收入情况中的%

73.1%

77.6%

51.3%

72.2%

总数的%

16.2%

47.4%

8.5%

农村户口

14

32

19

65

14.4

39.7

10.8

65.0

21.5%

49.2%

29.2%

26.9%

22.4%

48.7%

27.8%

6.0%

13.7%

8.1%

52

143

39

234

52.0

143.0

39.0

234.0

22.2%

61.1%

16.7%

卡方检验

值

df

渐进Sig.（双侧）

Pearson卡方

10.622a

2

.005

似然比

9.844

.007

线性和线性组合

4.077

1

.043

有效案例中的N

a.0单元格（0.0%）的期望计数少于5。

最小期望计数为10.83。

因为卡方值小于0.05拒绝原假设,认为行列变量之间相关,户口对未来收入看法有影响，说明城镇和农村储户对“未来收入状况的变化趋势”持不同的态度。

3、分析储户一次存款金额的分布，并对不同年龄段的储户进行比较。

由于存款金额数据为定距型变量，直接采用频数分析不利于对其分布形态的把握，因此考虑依据第三章中的数据分组功能对数据分组后再编制频数分布表。

转换→重新编码为不同变量→选择存（取）款金额，输出变量名称填存款金额分组，单击旧值和新值，对数据进行分组，分为0-500、501-2000、2001-3500、3501-5000、5000以上五个组。

最后点击确定。

再分析→描述统计→频率→变量：

存款金额分组，图表选择直方图，选择显示正态曲线。

最后输出下列图表：

存款金额分组

频率

百分比

有效百分比

累积百分比

有效

1.00

85

34.6

2.00

77

31.3

65.9

3.00

12

4.9

70.7

4.00

23

9.3

80.1

5.00

49

19.9

100.0

246

进行数据拆分，并计算不同年龄段储户的一次存款金额的四分位数，并通过四分位数比较分布上的差异。

步骤：

数据→拆分文件→分组方式：

年龄→确定。

分析→描述统计→频率→统计量→四分位数前打勾→确定。

输出如下图表：

统计量

20岁以下

N

缺失

百分位数

25

1.0000

50

3.0000

75

.

20~35岁

133

2.0000

4.0000

35~50岁

78

50岁以上

33

1.5000

分析储户一次存款金额的分布，并对不同年龄段的储户进行比较。

存款在500以下所占百分比最大，有34.6%，其次是500-1000的人数。

而存款在5000以上的也有19.9%，说明存款数额悬殊较大。

从输出图表中看出20-35年龄段的储户最多，其次是35-50岁年龄段，这两部分的人群存款意识比较强，20岁以下的储户只有2人，人数特别少，因为这一年龄段的人群大部分是学生，而50岁以上的老人可能更愿意把钱藏在家里而不是拿到银行去存。

第5题：

方差分析2

在某化工生产中为了提高收率，选了三种不同浓度，四种不同温度做试验。

在同一浓度与温度组合下各做两次试验，其收率数据如下面计算表所列（数据均已减去75）。

试在α=0.05显著性水平下分析：

（1）给出SPSS数据集的格式（列举前4个样本即可）；

（2）浓度对收率有无显著影响，并进行多重比较检验（只选用第1个检验指标）；

（3）浓度、温度以及它们间的交互作用对收率有无显著影响。

本道题重点考察我们对于在SPSS应用过程中对于方差分析的应用情况。

先将这组数据输入SPSS，然后进行两个方面的计算：

单因素方差分析和多因素方差分析。

利用SPSS的非必须功能，从而得出它们的方差数据，进而进行分析和结果的得出。

多重比较检验的方法：

LSD方法适用于各总体方差相等的情况，特点是比较灵敏；

Tukey方法和S-N-K方法适用于各水平下观测变量个数相等的情况；

Scheffe方法比Tukey方法不灵敏。

分别定义分组变量A、X、B，在变量视图与数据视图中输入表格数据

分析-比较均值-单因素ANOVA-因变量列表：

收率，因子列表：

浓度-确定。

单因素方差分析

收率

平方和

均方

F

显著性

组间

35.083

17.542

3.726

.041

组

98.875

21

4.708

总数

133.958

显著性=0.41小于0.05说明拒绝原假设（浓度对收益无显著影响），证明浓度对收益有显著影响。

分析-比较均值-单因素ANOVA-两两比较：

LSD-选项：

描述性-确定

输出：

描述

均值

标准差

标准误

均值的95%置信区间

极小值

极大值

下限

上限

8

11.2500

1.48805

.52610

10.0060

12.4940

9.00

13.00

8.7500

1.83225

.64780

7.2182

10.2818

6.00

11.00

3

11.3750

2.92465

1.03402

8.9299

13.8201

14.00

24

10.4583

2.41335

.49262

9.4393

11.4774

多重比较

因变量:

收率

LSD

（I）浓度

（J）浓度

均值差（I-J）

95%置信区间

2.50000*

1.08493

.032

.2438

4.7562

-.12500

.909

-2.3812

2.1312

-2.50000*

-4.7562

-.2438

-2.62500*

.025

-4.8812

-.3688

.12500

-2.1312

2.3812

2.62500*

.3688

4.8812

*.均值差的显著性水平为0.05。

上面有星号的说明有显著差异，即根据LCD算法，浓度1与浓度2具有显著差异，浓度3与浓度2有显著性差异，浓度1与浓度3差异性较小。

分析-一般线性模型-单变量-因变量：

收率，固定因子：

浓度、温度，-模型选择全因子-确定。

主体间因子

浓度

温度

6

4

主体间效应的检验

收率

源

III型平方和

Sig.

校正模型

69.458a

11

6.314

1.175

.391

截距

2625.042

488.380

.000

A

3.264

.074

B

14.792

4.931

.917

.462

A*B

19.583

.607

.721

误差

64.500

5.375

总计

2759.000

校正的总计

a.R方=.519（调整R方=.077）

结果表明，只有因子A（浓度）是显著的，即浓度不同将对收率产生显著影响，而温度及交互作用的影响都不显著，这说明要提高收率必须把浓度控制好。

方差分析可以很好的去辨别两个事物之间存在联系的紧密性。

通过数据，我们可以分辨出浓度的影响更加显著，从而做出调整。

第11题：

曲线回归3

根据收集的1981年至2000年的数据，分析教育支出受年人均可支配收入的影响。

（提示：

首先绘制两者的散点图。

再尝试选择二次、三次曲线、复合函数和幂函数模型，利用曲线估计进行本质线性模型分析。

）

思路：

本题主要考察曲线回归的容，先绘制两者散点图，再用二次、立方、复合、幂函数模型，进行分析。

图形→旧对话框→散点/点状→简单分布→Y轴：

教育支出，X轴：

年人均可支配收入→确定。

得到散点图如下：

分析→回归→曲线估计→因变量：

教育支出，自变量：

年人均可支配收入，个案标签：

年份，模型二次项、立方、幂、复合前打勾→确定。

得到以下图表：

模型汇总和参数估计值

教育支出

方程

模型汇总

参数估计值

R方

df1

df2

常数

b1

b2

b3

二次

.963

104.027

116.057

-.053

9.784E-006

三次

.964

62.555

7

190.569

-.102

1.831E-005

-4.370E-010

复合

.985

611.315

9

21.659

1.000

幂

.946

156.436

1.633

自变量为年人均可支配收入。

在二次、三次、复合、幂函数的模型中复合函数的R方是最大、最接近1的。

所以应用复合函数来表示年人均可支配收入与教育支出的函数关系。

根据函数图象看出，教育支出是随年人均可支配收入增长而增长的，说明随着人们可支配收入增加，对教育的关注更多，投入更多。

第12题：

聚类分析1

9个学生的数学、物理、化学、语文、历史、英语的成绩如下表。

要求做K-Means聚类分析，分成3类，初始类中心点由SPSS自行确定。

本题考察K聚类（快速聚类）的容，根据题目只要指定聚类数目K和确定K个初始类中心即可。

先把表格数据输入数据编辑器中。

分析→分类→K-均值聚类→变量中把数学、物理、化学、语文、历史、英语选进，聚类数为3→选项→初始聚类中心和ANOVA表前打勾→确定。

初始聚类中心

聚类

数学

83

67

物理

61

100

63

化学

72

79

语文

84

41

历史

81

英语

57

迭代历史记录a

迭代

聚类中心的更改

14.513

15.411

17.610

a.由于聚类中心没有改动或改动较小而达到收敛。

任何中心的最大绝对坐标更改为.000。

当前迭代为2。

初始中心间的最小距离为39.724。

最终聚类中心

74

70

68

92

71

64

60

69

56

ANOVA

66.194

35.417

1.869

.234

422.292

48.236

8.755

.017

105.000

113.333

.926

.446

570.028

74.694

7.631

.022

175.278

15.611

11.228

.009

255.292

39.236

6.507

.031

F检验应仅用于描述性目的，因为选中的聚类将被用来最大化不同聚类中的案例间的差别。

观测到的显著性水平并未据此进行更正，因此无法将其解释为是对聚类均值相等这一假设的检验。

每个聚类中的案例数

4.000

2.000

3.000

9.000