设计实例31系统在任意方波激励下的响应谱分析基本知识在工程Word文档格式.docx

设计实例31系统在任意方波激励下的响应谱分析基本知识在工程Word文档格式.docx

《设计实例31系统在任意方波激励下的响应谱分析基本知识在工程Word文档格式.docx》由会员分享，可在线阅读，更多相关《设计实例31系统在任意方波激励下的响应谱分析基本知识在工程Word文档格式.docx（13页珍藏版）》请在冰豆网上搜索。

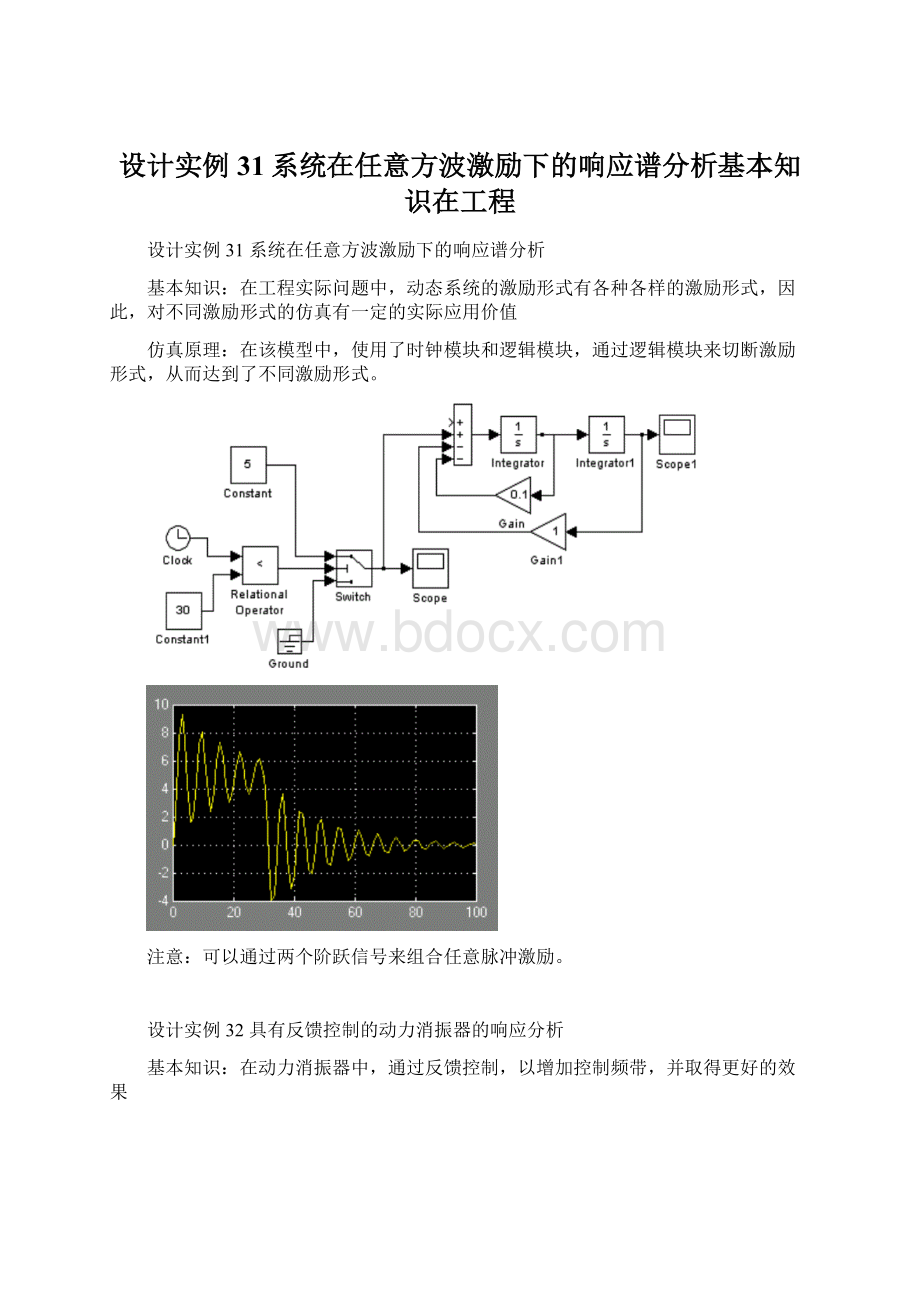
根据梁的动力学方程：

其中，

是作用在上的分布载荷。

在给定边界条件下，设系统的正则归一化模态函数为：

，取坐标变换为：

其中，

是主坐标：

并写成矩阵形式

代入动力学方程并利用模态函数的正交性，有：

写成有限矩阵形式：

其中：

，

设已知简支梁的长度

固有模态和频率为

频率为：

在中点作用一集中力

，作用时间为2秒，试求梁的响应

设计实例34信号的FFT变换

基本知识:

快速傅立叶变换（FFT）在动态系统中经常采用，它是将时间域信号经过FFT变换到频率域，分析信号的频率成分提供了工具。

本仿真采用脚本文件仿真。

%%FFT变换变换点

f1=20;

f2=40;

f3=60;

%%设置信号频率

f=1/f3/2.56%%设置采样频率（最底满足的采样频率）

t=0:

f:

1;

%%设置采样点序列

t1=0:

0.0001:

1%%设置较小的步长可得到较光滑的时间历程曲线

h=t/f;

%%频率分辨率

x1=2*sin（2*pi*f1*t1）+5*cos（2*pi*f2*t1）+20*sin（2*pi*f3*t1）;

%%时间历程

x=fft（x1）;

%%快速傅立叶变换

subplot（3,1,1）,plot（t1,x1）;

%%绘图时间历程

title（'

时间历程'

）%%标题

subplot（3,1,2）,plot（h（1:

length（h）/2）,abs（x（1:

length（h）/2）））;

%%傅立叶变换幅值

幅值'

）

subplot（3,1,3）,plot（h（1:

length（h）/2）,angle（x（1:

%%傅立叶辨率相位

title（'

相位）

设计实例35基于传递函数模型下任意激励下系统的响应

基本知识

仿真原理

%%任意激励下系统的响应

0.01:

5;

num1=[1001000];

num2=[1000];

den=[110100600];

sys1=tf（num1,den）

sys2=tf（num2,den）

y1=step（sys1,t）;

y2=step（sys2,t）;

%%%%%%

y3=impulse（sys1,t）;

u=3-t

y4=lsim（sys2,u,t）;

plot（t,y）;

plot（t,u）;

plot（t,y1,t,y2,t,y3,t,y4）;

grid

Unit-steprespontse'

'

fontsize'

20）

xlabel（'

t（scend）'

20'

ylabel（'

outpotputy'

text（0.07,2.8,'

x（t）'

text（0.7,2.35,'

y（t）'

设计实例36临界阻尼下质点能否越过平衡位置的仿真

根据振动理论可知，在临界阻尼状态下，不论怎么样给定初始条件，质点最多只有一次越过平衡位置。

在下图中，改变两个积分器的初始值（相当于给定初试速度和初试位移），观察示波器的输出信号

设计实例37高级积分器的应用

（1）--------弹性球的动力学问题

关于高级积分器（integrator）积分器除了使用默认情况外还有其他类型，

1定义外部初始条件（external）

在积分器的Initialconditionsources有两种选择（internalexternal），如果选择internal,则直接可以在initialcondition参数中设置初始值，但有时候在动态仿真过程中需要改变初始条件，这样就出现了外部条件源的设定方法，同时积分器的形状发生改变。

如右图所示。

2限制积分器

为了防止超出指定的范围，可以选择limitoutput复选框并在下面的框中填写范围，同时积分器的形状发生改变。

3重置积分器

在积分器的属性窗口当中有一个（externalreset）参数选择，分别是rising,（当重置信号有上升沿时触发状态重置）

falling,（当重置信号有下降沿时触发状态重置）

either（当重置上升信号或有下降信号时触发状态重置）

level（当重置信号为非零时，触发并保持输出信号为初始条件）

3状态端口状态端口的特点是：

如果状态端口在当前时间步上重置，那么状态端口的输出值是积分器还没有被重置时的积分器输出端口的值，也就是说，状态端口的输出值比积分器的输出端口早一个时间步。

正是这样的一个特点，往往可以把重置前的积分值作为以后的积分的初始条件。

创建自动重置积分器示例：

有一个弹性球，其恢复系数为k=0.8，（力学中的定义是碰撞结束和开始两个时刻的速度比称为恢复系数:

）,距离地面高度为h=10m的地方以初速度

垂直向上抛出，使对该问题进行仿真，并给出弹性球的运动规律。

仿真原理一次建模：

弹性小球在第一次接地前的动力学方程为：

，

弹性小球在以后的每次离开地面是，初速度应有所变化，但动力学方程形式不变。

1二次建模（仿真模型）由于设计到了初始条件的变化，则使用重置积分器模型

建立仿真框图如下，其中的积分器要设置成外部触发，显示端口，使用下降沿触发方式，其中的状态端口的特点是输出值比积分器的输出端口早一个时间步

请考虑如果计入空气阻尼（线性模型），该如建立二此模型？

设计实例38高级积分器应用

（2）

基本知识一次模型：

当输入的值等于5时改变积分初始值，使积分的初始值恢复到零状态。

在下图中，使用了高级积分器模型，使用加法器配合上升沿触发方式。

设计实例39高级积分器的应用（3）

在某些时候，需要对改变积分器的初始状态，以下问题为：

积分器的输入为1，初始条件为-50，如果积分值超过20，则将积分初始条件设置为-100。

仿真原理建立仿真框图如下，其中的积分器要设置成外部触发，显示端口，使用上升沿触发方式，其中的状态端口的特点是输出值比积分器的输出端口早一个时间步。

关于状态端口：

状态端口的特点是：

6．5版本7。

0版本

设计实例40非线性动力学控制问题

图示质量为m=5kg的小车在水平直线轨道上运动，不计摩擦，设小车上装有喷其式发动机，当小车的速度和位移之和为负时，启动左边的发动机，当小车的速度与位移之和为正时，启动右边的发动机，每一时刻只有一个发动机工作，射发动机在工作时的推力为常数1，开始的时候小车的位置为+12m，控制的目的使小车在原点位置，（该问题类似与卫星的位置的控制问题），使建立该问题大仿真模型，并记录下小车的位移响应曲线和小车能停止在原点的时间。

（1）建立系统的一次模型

即

其中

在该问题中采用了符号函数模块来实现加载过程，并采用了逻辑模块和时钟来记录小车的停止时的时间。

仿真模型如下。

可以得到最后停止的时间是62.7秒