长沙中考数学试题9年分类汇编统计与概率Word下载.docx

长沙中考数学试题9年分类汇编统计与概率Word下载.docx

《长沙中考数学试题9年分类汇编统计与概率Word下载.docx》由会员分享，可在线阅读，更多相关《长沙中考数学试题9年分类汇编统计与概率Word下载.docx（19页珍藏版）》请在冰豆网上搜索。

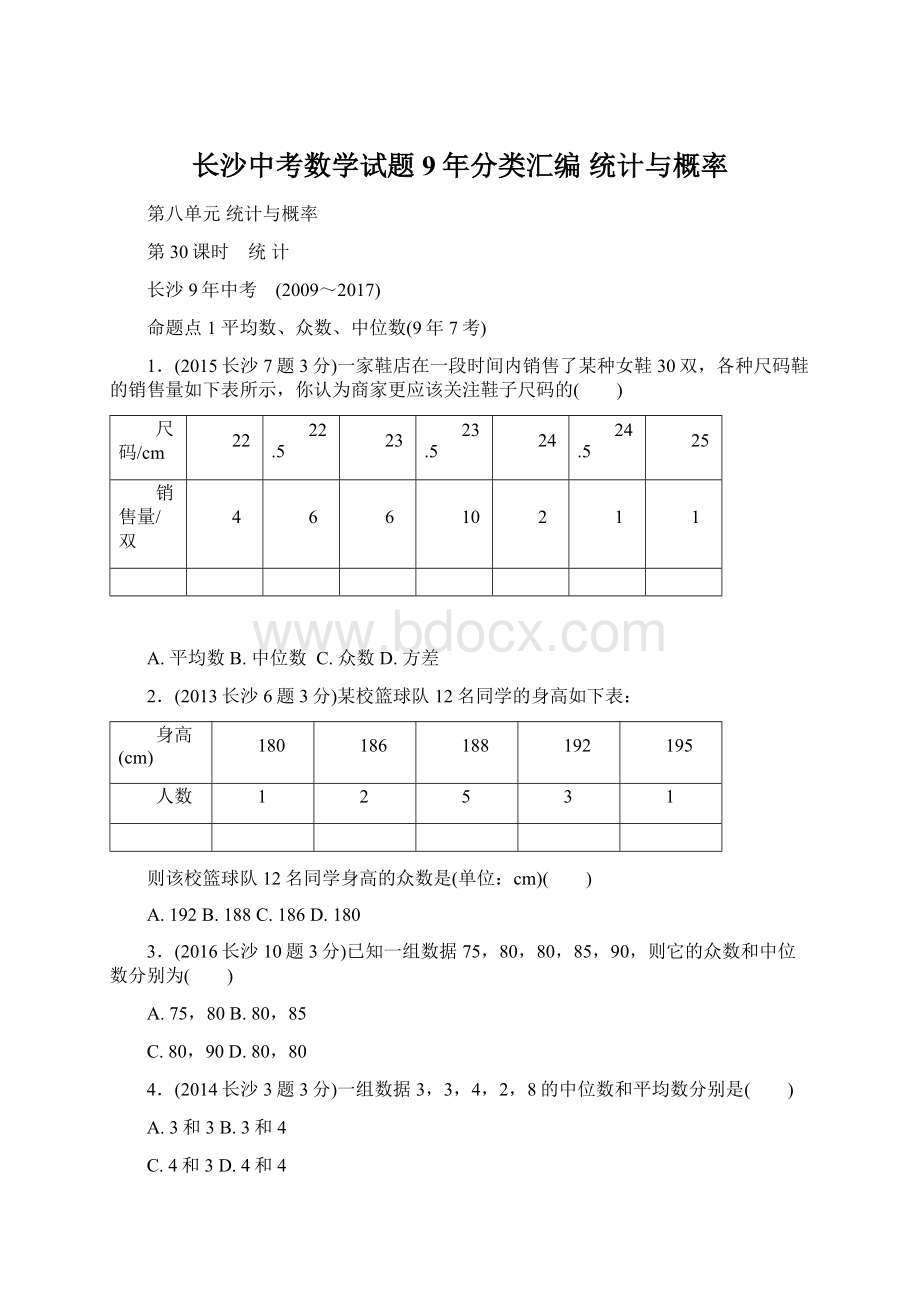
85

90

95

那么这9名学生所得分数的众数和中位数分别是（　　）

A.90，90B.90，85

C.90，87.5D.85，85

命题点2方差的意义（9年3考）

7．（2012长沙3题3分）甲、乙两学生在军训打靶训练中，打靶的总数相同，且所中环数的平均数也相同，但甲的成绩比乙的成绩稳定，那么两者方差的大小关系是（　　）

A．s

<

s

B．s

>

C．s

＝s

D．不能确定

8．（2017长沙17题3分）甲、乙两名同学进行跳高测试，每人10次跳高的平均成绩恰好是1.6米，方差分别是s

＝1.2，s

＝0.5，则在本次测试中，________同学的成绩更稳定．（填“甲”或“乙”）

9．下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：

甲

乙

丙

丁

平均数（cm）

185

方差

3.6

7.4

8.1

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（　　）

A.甲　　　B.乙　　　C.丙　　　D.丁

命题点3统计图（表）的分析（近9年仅2010年末考）

10．（2011长沙9题3分）谢老师对班上某次数学模拟考试成绩进行统计，绘制了如图所示的统计图，根据图中给出的信息，这次考试成绩达到A等级的人数占总人数的（　　）

第10题图

A.6%B.10%C.20%D.25%

11．（2011长沙21题8分）“珍惜能源从我做起，节约用电人人有责”．为了解某小区居民节约用电情况，物业公司随机抽取了今年某一天本小区10户居民的日用电量，数据如下：

用户序号

7

8

9

日用电量

（度）

4.4

4.0

5.0

5.6

3.4

4.8

5.2

4.2

（1）求这组数据的极差和平均数；

（2）已知去年同一天这10户居民的平均日用电量为7.8度，请你估计，这天与去年同日相比，该小区200户居民这一天共节约了多少度电？

12．（2016长沙21题8分）为积极响应市委市政府“加快建设天蓝·

水碧·

地绿的美丽长沙”的号召，我市某街道决定从备选的五种树中选购一种进行栽种，为了更好地了解社情民意，工作人员在街道辖区范围内随机抽取了部分居民，进行“我最喜欢的一种树”的调查活动（每人限选其中一种树），并将调查结果整理后，绘制成下面两个不完整的统计图：

第12题图

请根据所给信息解答以下问题：

（1）这次参与调查的居民人数为________；

（2）请将条形统计图补充完整；

（3）请计算扇形统计图中“枫树”所在扇形的圆心角度数；

（4）已知该街道辖区内现有居民8万人，请你估计这8万人中最喜欢玉兰树的有多少人？

13．（2015长沙21题8分）中华文明，源远流长；

中华汉字，寓意深广．为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩x/分

频数

频率

50≤x＜60

0.05

60≤x＜70

20

0.10

70≤x＜80

30

b

80≤x＜90

a

0.30

90≤x≤100

0.40

第13题图

请根据所给信息，解答下列问题：

（1）a＝________，b＝________；

（2）请补全频数分布直方图；

（3）这次比赛成绩的中位数会落在________分数段；

（4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人？

答案

1．C　【解析】对于商家而言，哪种尺码的鞋子销售量多，进货时就应偏向于进哪种尺码的鞋子，从而获得更多的利润．∵众数表示的是某组数据中出现次数最多的数，∴商家应该关注的是鞋子尺码的众数．

2．B　【解析】∵在一组数据中，出现次数最多的数是这组数据的众数，在这组数据中，188cm出现了5次，出现次数最多，∴这组数据的众数是188cm.

3．D　【解析】∵这组数据中出现次数最多的数是80，∴众数为80；

将这组数据从小到大（或从大到小）排列，处在中间的数是80，∴中位数为80.

4．B　【解析】平均数x＝

×

（2＋3＋3＋4＋8）＝4；

确定中位数时先把数据按照从小到大（或从大到小）的顺序重新排列，得出数据为2、3、3、4、8，∵这组数据最中间的数是3，∴中位数是3.

5．50　【解析】确定中位数时先把这60个数按照从小到大（或从大到小）的顺序排列，其中第30和31个数的平均数即为这组数据的中位数，由题意知这组数据的第30和第31个数均为50，∴这组数据的中位数为50.

6.A

7．A　【解析】两组数据如果平均数相同，方差较小的一组数据波动比较小．本题中甲的成绩稳定，∴甲的方差就比乙的方差小．

8．乙　【解析】要比较两名同学成绩谁更加稳定，即看两名同学成绩的方差谁更小，∵s

＝0.5，∴s

＞s

，∴乙同学的成绩更稳定．

9.A

10．C　【解析】∵由统计图可知A、B、C、D、E各等级的人数分别是10，15，12，10，3，∴五个等级总共50人，∴A等级的人数占总人数的百分比为

100%＝20%.

11．解：

（1）∵这组数据的最大值是5.6，最小值是3.4，

∴这组数据的极差为：

5.6－3.4＝2.2（度）；

……（2分）

这组数据的平均数为：

x＝

（4.4＋4.0＋5.0＋5.6＋3.4＋4.8＋3.4＋5.2＋4.0＋4.2）＝

＝4.4（度），

答：

这组数据的极差和平均数分别为2.2度和4.4度；

……（6分）

（2）200×

（7.8－4.4）＝680（度），

该小区200户居民这一天共节约了680度电．……（8分）

12．解：

（1）1000人；

【解法提示】∵由条形统计图可知最喜欢桂花树的人数为125人，由扇形统计图可知最喜欢桂花树的人数所占百分比为12.5%，∴这次参与调查的居民人数为125÷

12.5%＝1000（人）．

（2）补全条形统计图如解图所示：

……（4分）

【解法提示】参与调查的总人数减去各组的人数，即为最喜欢樟树的人数，即1000－250－375－125－100＝150（人）．

（3）∵由条形统计图可知最喜欢枫树的人数为100人，

∴最喜欢枫树的人数所占总人数百分比为

100%＝10%，

∴“枫树”所在扇形的圆心角度数为360°

10%＝36°

；

（6分）

（4）∵由条形统计图可知参与调查的居民中最喜欢玉兰树的人数为250人，

∴最喜欢玉兰树的人数占总人数百分比为

100%＝25%，

∴8×

25%＝2（万人）．

该街道辖区内最喜欢玉兰树的人数大约有2万人．（8分）

13．解：

（1）60，0.15；

……（2分）

【解法提示】由题意知样本容量为200，由统计表可知成绩在80≤x<

90分数段的频率为0.30，∴成绩在80≤x<

90分数段的频数a＝200×

0.30＝60；

由统计表可得成绩在70≤x<

80分数段的频数为30，∴其对应的频率b＝

＝0.15.

（2）由

（1）可知成绩在80≤x<

90的频数a＝60，补全频数分布直方图如解图所示：

……（4分）

（3）80≤x＜90；

……（6分）

【解法提示】频率累加情况如下：

∵0.05＋0.10＋0.15＝0.30＜0.5，∴中位数不在前三组中，∵0.05＋0.10＋0.15＋0.30＝0.60＞0.5，∴中位数在80≤x＜90这一分数段．

（4）由统计表可知样本中成绩在90分以上（包括90分）的频率为0.40，

∴3000×

0.40＝1200（人）．

该校参加这次比赛的3000名学生中成绩“优”等的人数约为1200人.

…………………………………………………………………………（8分）

第31课时　概率

命题点1事件的分类（9年4考）

1．（2010长沙4题3分）下列事件是必然事件的是（　　）

A．通常加热到100℃，水沸腾

B．抛一枚硬币，正面朝上

C．明天会下雨

D．经过城市中某一有交通信号灯的路口，恰好遇到红灯

2．（2015长沙8题3分）下列说法中正确的是（　　）

A．“打开电视机，正在播放《动物世界》”是必然事件

B．某种彩票的中奖概率为

，说明每买1000张彩票，一定有一张中奖

C．抛掷一枚质地均匀的硬币一次，出现正面朝上的概率为

D．想了解长沙市所有城镇居民的人均年收入水平，宜采用抽样调查

3.（2017长沙6题3分）下列说法正确的是（　　）

A.检测某批次灯泡的使用寿命，适宜用全面调查

B.可能性是1%的事件在一次试验中一定不会发生

C.数据3，5，4，1，－2的中位数是4

D.“367人中有2人是同月同日出生”为必然事件

4．（2012长沙15题3分）任意抛一枚硬币，则“正面朝上”是________事件．

5．下列说法中错误的是（　　）

A.掷一枚均匀的骰子，骰子停止转动后6点朝上是必然事件

B.了解一批电视机的使用寿命，适合用抽样调查的方式

C.若a是实数，则|a|<

0是不可能事件

D.甲、乙两人各进行10次射击，两人射击成绩的方差分别为s

＝2，s

＝4，且两人平均成绩相同则甲的射击成绩更稳定

命题点2概率的计算（必考）

6．（2014长沙15题3分）100件外观相同的产品中有5件不合格．现从中任意抽取1件进行检测，抽到不合格产品的概率是________．

7．（2015长沙13题3分）一个不透明的袋子中只装有3个黑球，2个白球，这些球的形状、大小、质地等完全相同，即除颜色外无其他差别，在看不到球的条件下，随机从袋中摸出1个球，则摸出白球的概率是________．

8．（2013长沙17题3分）在一个不透明的盒子中装有n个小球，它们只有颜色上的区别，其中有2个红球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复实验后发现，摸到红球的频率稳定于0.2，那么可以推算出n大约是________．

9．（2016长沙18题3分）若同时抛掷两枚质地均匀的骰子，则事件“两枚骰子朝上的点数互不相同”的概率是________．

10．（2009长沙7题3分）从某玉米种子中抽取6批，在同一条件下进行发芽试验，有关数据如下：

种子粒数

100

400

800

1000

2000

5000

发芽种子粒数

298

652

793

1604

4005

发芽频率

0.850

0.745

0.815

0.793

0.802

0.801

根据以上数据估计该玉米种子发芽的概率约为________（精确到0.1）．

11．（2010长沙20题6分）有四张完全一样的空白纸片，在每张纸片的一个面上分别写上1、2、3、4.某同学把这四张纸片写有字的一面朝下，先洗匀随机抽出一张，放回洗匀后，再随机抽出一张，求抽出的两张纸片上的数字之积小于6的概率．（用树状图或列表法求解）

12．在－1，1，2这三个数中，任选2个数分别作为点P的横坐标和纵坐标，过点P画双曲线y＝

，则该双曲线位于第一、三象限的概率是________．

13．某校决定从两名男生和三名女生中选出两名同学作为兰州国际马拉松赛的志愿者，则选出一男一女的概率是________．

命题点3统计与概率结合（9年5考）

14．（2009长沙20题6分）为了提高返乡农民工再就业能力，劳动和社会保障部门对400名返乡农民工进行了某项专业技能培训，为了解培训的效果，培训结束后随机抽取了部分参训人员进行技能测试，测试结果划分成“不合格”、“合格”、“良好”、“优秀”四个等级，并绘制了如图所示的统计图，请根据统计图提供的信息，回答下列问题：

第14题图

（1）培训结束后共抽取了________名参训人员进行技能测试；

（2）从参加测试的人员中随机抽取一人进行技能展示，其测试结果为“优秀”的概率为________；

（3）估计这400名参加培训的人员中，获得“优秀”的总人数大约是多少？

15．（2014长沙21题8分）某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的长沙——我最喜爱的长沙小吃”调查活动，将调查问卷整理后绘制成如图所示的不完整条形统计图．

调查问卷：

在下面四种长沙小吃中，你最喜爱的是（　　）（单选）

A.臭豆腐

B.口味虾

C.唆螺

D.糖油粑粑

第15题图

（1）请补全条形统计图；

（2）若全校有2000名同学，请估计全校同学中最喜爱“臭豆腐”的同学有多少人？

（3）在一个不透明的口袋中有四个完全相同的小球，把它们分别标号为四种小吃的序号A、B、C、D，随机地摸出一个小球然后放回，再随机地摸出一个小球．请用列表或画树状图的方法，求出恰好两次都摸到“A”的概率．

16．（2013长沙21题8分）“宜居长沙”是我们的共同愿景，空气质量倍受人们关注．我市某空气质量监测站点检测了该区域每天的空气质量情况，统计了2013年1月份至4月份若干天的空气质量情况，并绘制了如下两幅不完整的统计图．请根据图中信息，解答下列问题：

第16题图

（1）统计图共统计了________天的空气质量情况；

（2）请将条形统计图补充完整，并计算空气质量为“优”所在扇形的圆心角度数；

（3）从小源所在班级的40名同学中，随机选取一名同学去该空气质量监测站点参观，则恰好选到小源的概率是多少？

17．（2012长沙21题8分）某班数学课代表小华对本班上学期期末考试数学成绩（成绩取整数，满分为100分）作了统计分析，绘制成如下频数、频率统计表和频数分布直方图，请你根据图表提供的信息，解答下列问题：

分组

49.5～

59．5

59.5～

69．5

69.5～

79．5

79.5～

89．5

89.5～

100．5

合计

16

50

0.04

0.16

0.32

第17题图

（1）频数、频率统计表中a＝______，b＝_______；

（2）补全频数分布直方图；

（3）小华在班上任选一名同学，该同学数学成绩不低于80分的概率是多少？

18.（2017长沙21题8分）为了传承中华优秀传统文化，市教育局决定开展“经典诵读进校园”活动，某校团委组织八年级100名学生进行“经典诵读”选拔赛，赛后对全体参赛学生的成绩进行整理，得到下列不完整的统计图表．

组别

分数段

频次

A

60≤x<

70

17

0.17

B

70≤x<

C

80≤x<

0.45

D

90≤x<

0.08

第18题图

请根据所给信息，解答以下问题：

（1）表中a＝________，b＝________；

（2）请计算扇形统计图中B组对应扇形的圆心角的度数；

（3）已知有四名同学均取得98分的最好成绩，其中包括来自同一班级的甲、乙两名同学，学校将从这四名同学中随机选出两名参加市级比赛，请用列表法或画树状图法求甲、乙两名同学都被选中的概率．

1．A　2.D　3.D　4.随机　5.A

命题点2概率的计算（必考）

6.

　7.

　8.10　

9.

　【解析】列表如下：

　第二枚

第一枚　　

（1，1）

（1，2）

（1，3）

（1，4）

（1，5）

（1，6）

（2，1）

（2，2）

（2，3）

（2，4）

（2，5）

（2，6）

（3，1）

（3，2）

（3，3）

（3，4）

（3，5）

（3，6）

（4，1）

（4，2）

（4，3）

（4，4）

（4，5）

（4，6）

（5，1）

（5，2）

（5，3）

（5，4）

（5，5）

（5，6）

（6，1）

（6，2）

（6，3）

（6，4）

（6，5）

（6，6）

共有36种等可能的情况，两枚骰子朝上点数互不相同的情况有30种，∴两枚骰子朝上的点数互不相同的概率为

＝

.

10．0.8　【解析】∵在相同条件下，试验次数越多，越能较好地估计概率，∴种子粒数为5000时的发芽频率用于统计该玉米发芽的概率更合理，于是估计该玉米种子发芽的概率为0.801，精确到0.1为0.8.

画树状图如解图：

……（3分）

共有16种等可能的结果，两数之积小于6的情况有8种，

∴P（两数之积小于6）＝

.……（6分）

12.

　【解析】∵在－1，1，2这三个数中任选2个数分别作为P点的横坐标和纵坐标，∴符合要求的点有6个：

（－1，1），（－1，2），（1，2），（1，－1），（2，1），（2，－1），又∵该双曲线位于第一、三象限时，xy＝k＞0，只有2个：

（1，2），（2，1）符合题意，∴该双曲线位于第一、三象限的概率是

13.

　【解析】画树状图如解图：

由树状图可知共有20种等可能的结果，其中选择一男一女有12种情况，则选出一男一女的概率是

14．解：

（1）40；

【解法提示】培训结束后抽取了2＋12＋16＋10＝40名参训人员进行技能测试．

（2）

【解法提示】测试结果为“优秀”的概率为

（3）400×

＝100（人）．

获得“优秀”的总人数大约是100人．……（6分）

15．解：

（1）补全条形统计图如解图①所示：

【解法提示】样本容量减去臭豆腐、口味虾和糖油粑粑的频数，等于唆螺的频数，即50－（14＋21＋5）＝10（人）．

（2）14÷

50＝0.28＝28%，即样本中最喜爱“臭豆腐”一组占样本容量的百分比是28%，……（3分）

∴估计总体中最喜爱“臭豆腐”的人数是2000×

28%＝560（人）；

……（5分）

（3）画树状图，如解图②所示：

……（6分）

或列表如下：

第二次

第一次

AA

AB

AC

AD

BA

BB

BC

BD

CA

CB

CC

CD

DA

DB

DC

DD

……（7分）

共有16种等可能结果，其中两次都是A的情况只有1种，

∴恰好两次都摸到A的概率是P（A）＝

.……（8分）

16．解：

（1）100；

……（6分）

【解法提示】100×

20%＝20（天）．

空气质量为“优”所在扇形的圆心角度数为360°

20%＝72°

（3）根据题意得：

共有40种等可能情况，其中恰好选到小源有1种情况，

∴根据概率公式可知：

P（小源）＝

17．解：

（1）8，0.08；

（2分）

（2）补全频数分布直方图如解图所示：

共有50种等可能情况，其中抽到成绩不低于80分有20种情况，

∴P（成绩不低于80分）＝

＝0.4.（8分）

18.解：

（1）0.3，45；

【解法提示】∵共调查了100名学生，

∴B组的频率为a＝30÷

100＝0.3，C组的频数b＝100×

0.45＝45.

（2）∵B组的频率为0.3，

∴B组所对应的扇形圆心角度数为360°

0.3＝108°

（4分）

（3）设另外两名同学为A、B，列表如下：

乙甲

A甲

B甲

甲乙

A乙

B乙

甲A

乙A

甲B

乙B

由列表可知，共有12种等可能情况，其中甲、乙都被选中的情况有2种，

∴P（甲乙都被选中）＝