人教版初中数学第20章 数据的分析 全章表格式教案.docx

人教版初中数学第20章 数据的分析 全章表格式教案.docx

《人教版初中数学第20章 数据的分析 全章表格式教案.docx》由会员分享，可在线阅读，更多相关《人教版初中数学第20章 数据的分析 全章表格式教案.docx（42页珍藏版）》请在冰豆网上搜索。

人教版初中数学第20章数据的分析全章表格式教案

第二十章数据的分析

§20、1平均数

（一）

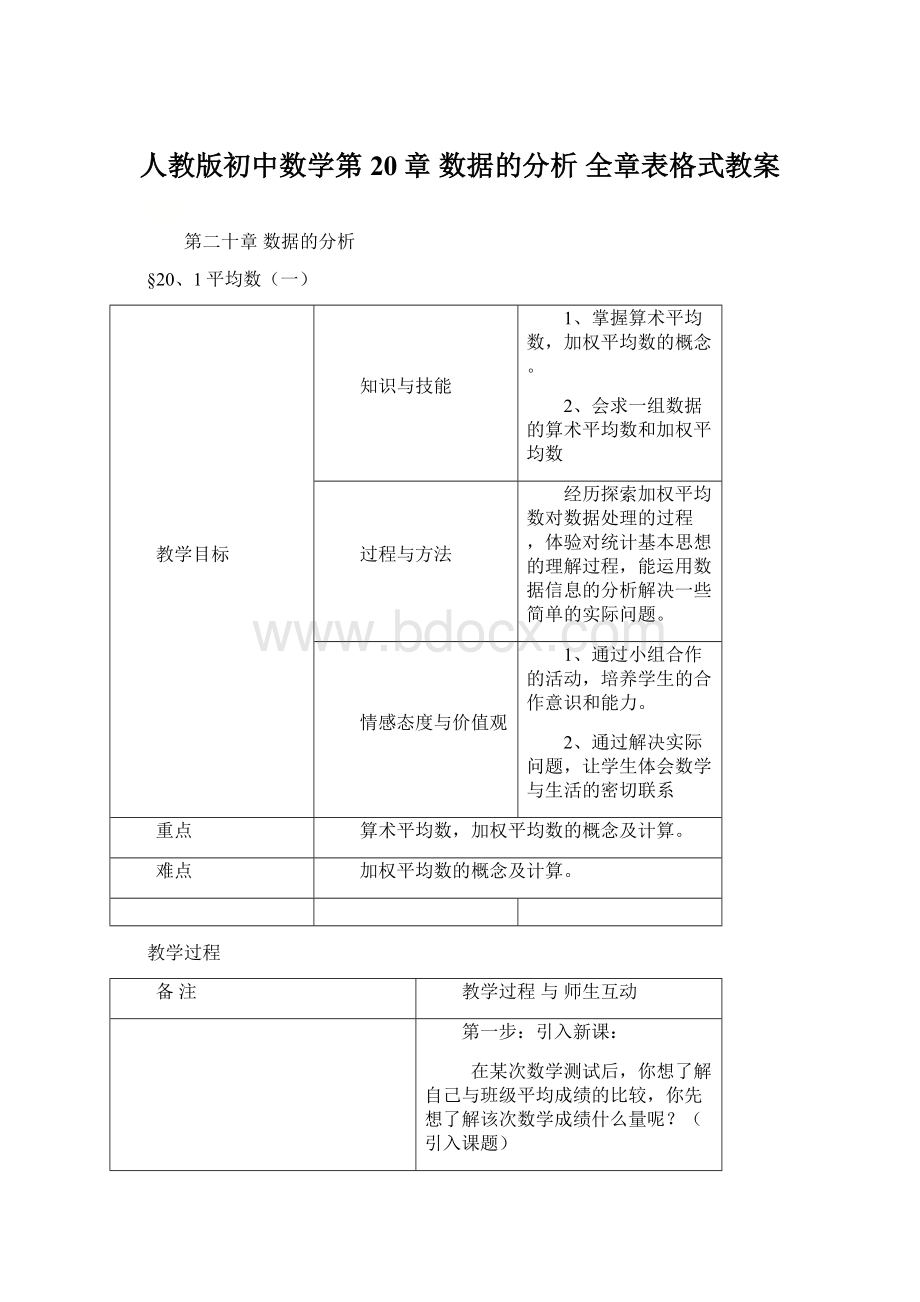
教学目标

知识与技能

1、掌握算术平均数，加权平均数的概念。

2、会求一组数据的算术平均数和加权平均数

过程与方法

经历探索加权平均数对数据处理的过程，体验对统计基本思想的理解过程，能运用数据信息的分析解决一些简单的实际问题。

情感态度与价值观

1、通过小组合作的活动，培养学生的合作意识和能力。

2、通过解决实际问题，让学生体会数学与生活的密切联系

重点

算术平均数，加权平均数的概念及计算。

难点

加权平均数的概念及计算。

教学过程

备注

教学过程与师生互动

第一步：

引入新课：

在某次数学测试后，你想了解自己与班级平均成绩的比较，你先想了解该次数学成绩什么量呢？

（引入课题）

第二步：

讲授新课：

1、引例：

下面是某班30位同学一次数学测试的成绩，各小组讨论如何求出它们的平均分：

95、99、87、90、90、86、99、100、95、87、88、86、94、92、90、95、87、86、88、86、90、90、99、80、87、86、99、95、92、92

甲小组：

X==91（分）

甲小组做得对吗？

有不同求法吗？

乙小组：

X=×××××××

=91（分）

乙小组的做法可以吗？

还有不同求法吗？

丙小组：

先取一个数90做为基准a，则每个数分别与90的差为：

5、9、-3、0、0、-4、……、2、2

求出以上新的一组数的平均数X'=1

所以原数组的平均数为X=X'+90=91

想一想，丙小组的计算对吗？

2、议一议：

问：

求平均数有哪几种方法？

①平均数：

一般地，如果有n个数x1，x2，……，xn，那么，叫做这n个数的平均数，读作“x拔”。

②加权平均数：

如果n个数中，x1出现f1次,x2出现f2次，……，xk出现fk次，（这里f1+f2+……+fk=n），那么，根据平均数的定义，这n个数的平均数可以表示为　这样求得的平均数叫做加权平均数，其中f1，f2，……,fk叫做权。

③利用基准求平均数X=X'+a

问：

以上几种求法各有什么特点呢？

公式

（1）适用于数据较小，且较分散。

公式

（2）适用于出现较多重复数据。

公式（3）适用于数据较为接近于某一数据。

第三步：

实际应用

练习：

P213利用计算器

（1）计算两支球队的平均身高，哪支球队队员的身材更为高大？

（2）计算两支球队的平均年龄，哪支球队队员的年龄更为年轻？

　例1：

某学校要了解期末数学考试成绩，从考试卷中抽取部分试卷，其中有一人得100分，2人得95分，8人得90分，10人得80分，15人得70分。

求这些同学的平均成绩。

　　分析：

这个平均数是加权平均数。

　　解：

平均成绩:

x=36（100×1+95×2+90×8＋80×10＋70×15）≈79.4

　　例2：

某同学使用计算器求30个数据的平均数时，错将其中的一个数据105输入为15，那么由此求出的平均数与实际平均数的差是______。

　　解：

由一组数据的平均数定义知

　　实际平均数:

x=（x1+x2+……+x29+105）

　　求出的平均数:

x错=（x1+x2+……+x29+15）

　　错-==-3

　　所以由此错误求出的平均数与实际平均数的差是-3。

　　提示：

解此类题一定要对平均数的定义十分清楚。

　　例3：

设两组数a1,a2,a3……an和b1,b2,b3……bn的平均数为和，那么新的一组数a1+b1,a2+b2,a3+b3……an+bn的平均数是[　　]

　　A.（+）　　B.+　　C.（+）　　D.以上都不对

　　错解：

好像是（A）

　　正解：

根据平均数的定义应选（B）

第四步：

随堂练习：

1、老师在计算学期总平均分的时候按如下标准:

作业占100%、测验占30%、期中占35%、期末考试占35%，小关和小兵的成绩如下表：

学生

作业

测验

期中考试

期末考试

小关

80

75

71

88

小兵

76

80

68

90

2、为了鉴定某种灯泡的质量，对其中100只灯泡的使用寿命进行测量，结果如下表：

（单位：

小时）

寿命

450

550

600

650

700

只数

20

10

30

15

25

求这些灯泡的平均使用寿命？

答案：

1.=79.05=802.=597.5小时

第五步：

课后练习：

1、在一个样本中，2出现了x次，3出现了x次，4出现了x次，5出现了x次，则这个样本的平均数为.

2、某人打靶，有a次打中环，b次打中环，则这个人平均每次中靶环。

3、一家公司打算招聘一名部门经理，现对甲、乙两名应聘者从笔试、面试、实习成绩三个方面表现进行评分，笔试占总成绩20%、面试占30%、实习成绩占50%，各项成绩如表所示：

应聘者

笔试

面试

实习

甲

85

83

90

乙

80

85

92

试判断谁会被公司录取，为什么？

4、在一次英语口试中，已知50分1人、60分2人、70分5人、90分5人、100分1人，其余为84分。

已知该班平均成绩为80分，问该班有多少人？

答案：

1.2.3.=86.9=96.5乙被录取4.39人

小结与反思：

20.1.1平均数

（二）

教学目标

知识与技能

1、加深对加权平均数的理解

2、会根据频数分布表求加权平均数，从而解决一些实际问题

3、会用计算器求加权平均数的值

过程与方法

经历探索加权平均数的应用过程，体验和理解统计的基本思想，学会频数分布表中应用加权平均数的方法。

情感态度与价值观

乐于接触社会环境中的数学信息，了解数学对促进社会进步和发展人类理解精神的作用。

重点

根据频数分布表求加权平均数

难点

根据频数分布表求加权平均数

教学过程

备注

教学设计与师生互动

第一步：

课堂引入

设计的几个问题如下：

（1）、请同学读P140探究问题，依据统计表可以读出哪些信息

（2）、这里的组中值指什么，它是怎样确定的？

（3）、第二组数据的频数5指什么呢？

（4）、如果每组数据在本组中分布较为均匀，比组数据的平均值和组中值有什么关系。

第二步：

应用举例：

例1：

为了解5路公共汽车的运营情况，公交部门统计了某天5路公共汽车每个运行班次的载客量，得到下表：

载客量/人

组中值

频数（班次）

1≤x＜21

11

3

21≤x＜41

31

5

41≤x＜61

51

20

61≤x＜81

71

22

81≤x＜101

91

18

101≤x＜121

111

15

这天5路公共汽车平均每班的载客量是多少？

分析：

根据上面的频数分布表求加权平均数时，统计中常用的各组的组中值代表各组的实际数据，把各组频数看作相应组中值的权。

例如在1≤x＜21之间的载客量近似地看作组中值11，组中值11的权是它的频3，由此这天5路公共汽车平均每班的载客量是:

思考：

从表中，你能知道这一天5路公共汽车大约有多少班次的载客量在平均载客量以上吗？

占全天总班次的百分比是多少？

分析：

由表格可知，81≤x＜101的18个班次和101≤x＜121的15个班次共有33个班次超过平均载客量，占全天总班次的百分比为33/83等于39.8％

活动：

使用计算器说明，操作时需要参阅计算器的使用说明书，通常需要先按动有关键，使计算器进入统计状态；然后依次输入数据x1，x2，…，xn，以及它们的权f，f2，…，fn；最后按动求平均数的功能键（例如键），计算器便会求出平均数的值。

例2：

下表是校女子排球队队员的年龄分布：

年龄

13

14

15

16

频数

1

4

5

2

求校女子排球队队员的平均年龄（可使用计算器）。

解：

答：

校女子排球队队员的平均年龄为14.7岁

所用时间t（分钟）

人数

0＜t≤10

4

0＜≤

6

20＜t≤20

14

30＜t≤40

13

40＜t≤50

9

50＜t≤60

4

第三步：

课堂练习：

1、某校为了了解学生作课外作业所用时间的情况，对学生作课外作业所用时间进行调查，下表是该校初二某班50名学生某一天做数学课外作业所用时间的情况统计表

（1）、第二组数据的组中值是多少？

（2）、求该班学生平均每天做数学作业所用时间

2、某班40名学生身高情况如下图，

请计算该班学生平均身高

答案1.

（1）.15.

（2）28.2.165

第四步：

课后练习：

1、某公司有15名员工，他们所在的部门及相应每人所创的年利润如下表

部门

A

B

C

D

E

F

G

人数

1

1

2

4

2

2

5

每人创得利润

20

5

2.5

2

1.5

1.5

1.2

该公司每人所创年利润的平均数是多少万元？

2、下表是截至到2002年费尔兹奖得主获奖时的年龄，根据表格中的信息计算获费尔兹奖得主获奖时的平均年龄？

年龄

频数

28≤X＜30

4

30≤X＜32

3

32≤X＜34

8

34≤X＜36

7

36≤X＜38

9

38≤X＜40

11

40≤X＜42

2

3、为调查居民生活环境质量，环保局对所辖的50个居民区进行了噪音（单位：

分贝）水平的调查，结果如下图，求每个小区噪音的平均分贝数。

答案：

1.约2.95万元2.约29岁3.60.54分贝

第五步：

课堂小结：

1、体会运用样本平均数去估计总体平均数的意义.

2、会运用样本平均数估计总体平均数

3、增强数学应用意识

课后反思：

20.1数据的代表

20.1.2中位数和众数

（一）

教学目标

知识与技能

1、认识中位数和众数，并会求出一组数据中的众数和中位数。

2、理解中位数和众数的意义和作用。

它们也是数据代表，可以反映一定的数据信息，帮助人们在实际问题中分析并做出决策。

3、会利用中位数、众数分析数据信息做出决策。

过程与方法

经历探索中位数、众数的概念的过程，学会根据数据做出总体的初步的思想、合理论证，领会平均数、中位数、众数的特征数的联系和区别。

情感态度与价值观

培养学生良好的数字信息处理的意识，建立学好数学的自信心，体会发展的内涵与价值。

重点

认识中位数、众数这两种数据代表

难点

利用中位数、众数分析数据信息做出决策。

教学过程

备注

教学设计与师生互动

第一步：

课前引入：

前面已经和同学们研究过了平均数的这个数据代表。

它在分析数据过程中担当了重要的角色，今天我们来共同研究和认识数据代表中的新成员——中位数和众数，看看它们在分析数据过程中又起到怎样的作用。

请同学们看下面问题：

　NO1、　一家鞋店在一段时间内销售了某种女鞋30双,其中各种尺码的鞋的销售量如下表所示:

鞋的尺码

（单位:

厘米）

22

22．5

23

23．5

24

24．5

25

销售量

（单位:

双）

1

2

5

11

7

3

1

在这个问题里，鞋店比较关心的是哪种尺码的鞋销售得最多．

师引导学生观察表格，并思考表格反映的是多少个数据的全体．（

NO2、在一次数学竞赛中，5名学生的成绩从低分到高分排列庆次是：

　　 5557616298

　　教师引导学生观察在这