高考全国1卷数学文文档格式.docx

高考全国1卷数学文文档格式.docx

《高考全国1卷数学文文档格式.docx》由会员分享，可在线阅读，更多相关《高考全国1卷数学文文档格式.docx（12页珍藏版）》请在冰豆网上搜索。

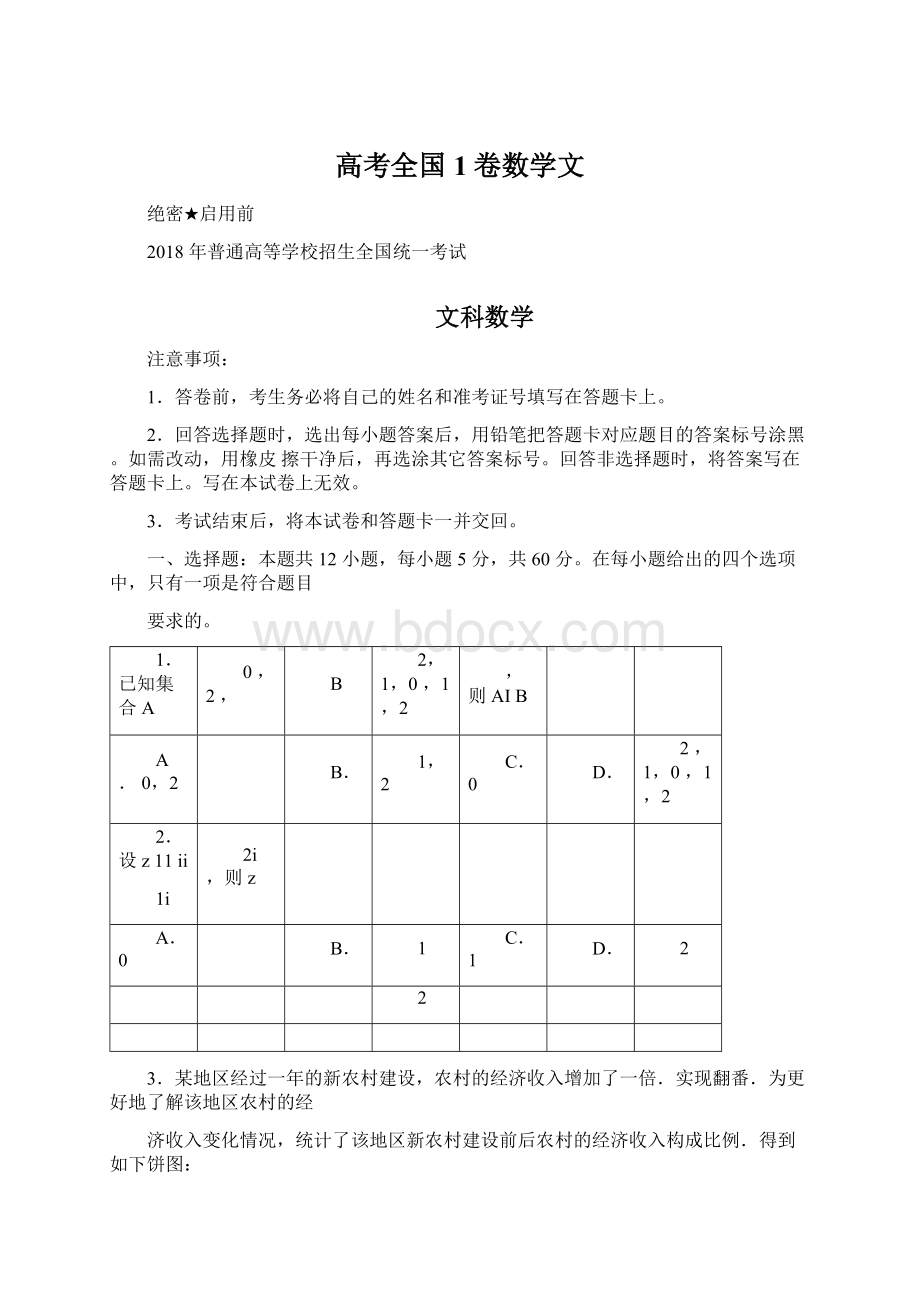
2．设z11ii

1i

2i，则z

A．0

1

C．1

2

3．某地区经过一年的新农村建设，农村的经济收入增加了一倍．实现翻番．为更好地了解该地区农村的经

济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例．得到如下饼图：

则下面结论中不正确的是

A．新农村建设后，种植收入减少

B．新农村建设后，其他收入增加了一倍以上

C．新农村建设后，养殖收入增加了一倍

D．新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半

方形，则该圆柱的表面积为

体积为

11．已知角的顶点为坐标原点，始边与x轴的非负半轴重合，终边上有两点A1，a，B2，b，且

则△ABC的面积为

都必须作答。

第22、23题为选考题，考生根据要求作答。

一）必考题：

共60分。

17．（12分）

18．（12分）

如图，在平行四边形ABCM中，ABAC3，∠ACM90，以AC为折痕将△ACM折起，使点M到达点D的位置，且AB⊥DA．

（1）证明：

平面ACD⊥平面ABC；

2

（2）Q为线段AD上一点，P为线段BC上一点，且BPDQDA，求三棱锥QABP的体积．

3

19．（12分）

某家庭记录了未使用节水龙头50天的日用水量数据（单位：

m3）和使用了节水龙头50天的日用水量

数据，得到频数分布表如下：

未使用节水龙头50天的日用水量频数分布表

日用

水量

0，0.1

0.1，0.2

0.2，0.3

0.3，0.4

0.4，0.5

0.5，0.6

0.6，0.7

频数

4

9

26

5

使用了节水龙头50天的日用水量频数分布表

0.1，0.2

0.2，0.3

13

10

16

1）在答题卡上作出使用了节水龙头50天的日用水量数据的频率分布直方图：

（2）估计该家庭使用节水龙头后，日用水量小于0.35m3的概率；

（3）估计该家庭使用节水龙头后，一年能节省多少水？

（一年按365天计算，同一组中的数据以这组

数据所在区间中点的值作代表．）

20．（12分）

设抛物线C：

y22x，点A2，0，B2，0，过点A的直线l与C交于M，N两点．

（1）当l与x轴垂直时，求直线BM的方程；

（2）证明：

∠ABM

∠ABN．

21．（12分）

x

已知函数fxae

lnx1．

（1）设x2是fx

的极值点．求a，并求fx的单调区间；

1

（2）证明：

当a≥时，fx≥0．

e

（二）选考题：

共10分。

请考生在第22、23题中任选一题作答。

如果多做，则按所做的第一题计分。

22．［选修4—4：

坐标系与参数方程］（10分）

在直角坐标系xOy中，曲线C1的方程为ykx2．以坐标原点为极点，x轴正半轴为极轴建立极坐

标系，曲线C2的极坐标方程为22cos30．

（1）求C2的直角坐标方程；

学科*网

（2）若C1与C2有且仅有三个公共点，求C1的方程．

23．［选修4—5：

不等式选讲］（10分）

已知fxx1ax1．

（1）当a1时，求不等式fx1的解集；

2）若x∈0，1时不等式fxx成立，求a的取值范围．

文科数学试题参考答案

一、选择题

1．A

2．C

3．A

4．C

5．B

6．D

7．A

8．B

9．B

10．C

11．B

12．D

二、填空题

13．-7

14．6

15．22

23

16．

三、解答题

17．解：

（1）由条件可得an+1=2（n1）an．n

将n=1代入得，a2=4a1，而a1=1，所以，a2=4．

将n=2代入得，a3=3a2，所以，a3=12．

从而b1=1，b2=2，b3=4．

（2）{bn}是首项为1，公比为2的等比数列．

由条件可得an12an，即bn+1=2bn，又b1=1，所以{bn}是首项为1，公比为2的等比数列．n1n

（3）由

（2）可得an2n1，所以an=n·

2n-1．

n

18．解：

（1）由已知可得，BAC=90°

，BA⊥AC．

又BA⊥AD，所以AB⊥平面ACD．

又AB平面ABC，

所以平面ACD⊥平面ABC．

2）由已知可得，DC=CM=AB=3，DA=32．

又BPDQ2DA，所以BP22．

作QE⊥AC，垂足为E，则QEP1DC．

由已知及

（1）可得DC⊥平面ABC，所以QE⊥平面ABC，QE=1．

因此，三棱锥QABP的体积为

S△ABP111322sin451．

32

2）根据以上数据，该家庭使用节水龙头后50天日用水量小于0.35m3的频率为

0.2×

0.1+1×

0.1+2.6×

0.1+2×

0.05=0.48，因此该家庭使用节水龙头后日用水量小于0.35m3的概率的估计值为0.48．

（3）该家庭未使用节水龙头50天日用水量的平均数为

x1（0.0510.1530.2520.3540.4590.55260.655）0.48．

50

该家庭使用了节水龙头后50天日用水量的平均数为

1x2（0.0510.1550.25130.35100.45160.555）0.35．

估计使用节水龙头后，一年可节省水（0.480.35）36547.45（m3）．

20．解：

（1）当l与x轴垂直时，l的方程为x=2，可得M的坐标为（2，2）或（2，–2）．所以直线BM的方程为y=1x1或y1x1．

22

（2）当l与x轴垂直时，AB为MN的垂直平分线，所以∠ABM=∠ABN．

当l与x轴不垂直时，设l的方程为yk（x2）（k0），M（x1，y1），N（x2，y2），则x1>

0，x2>

0．

yk（x2），2

y22x得ky2–2y–4k=0，可知y1+y2=k2，y1y2=–4．

BN的斜率之和为

kBM

kBN

y1

y2

x12

x2

将x1

2，x2

k

x2y1

x1y2

2（y1

y2）

直线

BM，

所以

x2y1x1y22（y1y2）．①

2（x12）（x22）

2及y1+y2，y1y2的表达式代入①式分子，可得

2y1y24k（y1y2）

880．k

kBM+kBN=0，可知BM，

BN

的倾斜角互补，

所以∠ABM+∠ABN．

综上，∠ABM=∠ABN．

12ex

1x

从而f（x）=2elnx1，f′（x）=

2e22e

当0<

x<

2时，f′（x）<

0；

当x>

2时，f′（x）>

2）当a≥1

lnx1，则g（x）

1时，g

x）<

时，g′（x）>

0．所以x=1是g（x）的最小值点．

故当x>

0时，gx）≥g

（1）=0．

f（x）0．

22．［选修4-4：

坐标系与参数方程

］（10分）

解：

（1）由xcos，ysin得C2的直角坐标方程为

（x1）2y24．

2）由

（1）知C2是圆心为

A（1,0），半径为2的圆．

且关于y轴对称的两条射线．记y轴右边的射线为

l2．由于B在圆C2的外面，故C1与C2有且仅有三个公共点等价于l1与C2只有

两个公共点，或l2与C2只有一个公共点且l1与C2有两个公共点．

|k2|4

当l1与C2只有一个公共点时，A到l1所在直线的距离为2，所以22，故k4或k0．

121k213

经检验，当k0时，l1与C2没有公共点；

当k3时，l1与C2只有一个公共点，l2与C2有两个公共

点．

|k2|4

当l2与C2只有一个公共点时，A到l2所在直线的距离为2，所以22，故k0或k．

k213

经检验，当k0时，l1与C2没有公共点；

当k3时，l2与C2没有公共点．学.科网

综上，所求C1的方程为y34|x|2．

23．[选修4-5：

不等式选讲]（10分）

2,x1,

（1）当a1时，f（x）|x1||x1|，即f（x）2x,1x1,

2,x1.

故不等式f（x）1的解集为{x|x}．

（2）当x（0,1）时|x1||ax1|x成立等价于当x（0,1）时|ax1|1成立．

若a0，则当x（0,1）时|ax1|1；

若a0，|ax1|1的解集为0x，所以1，故0a2．

aa

综上，a的取值范围为（0,2]．

因此，当a时，