整理偏微分方程与积分变换Word格式文档下载.docx

整理偏微分方程与积分变换Word格式文档下载.docx

《整理偏微分方程与积分变换Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《整理偏微分方程与积分变换Word格式文档下载.docx（15页珍藏版）》请在冰豆网上搜索。

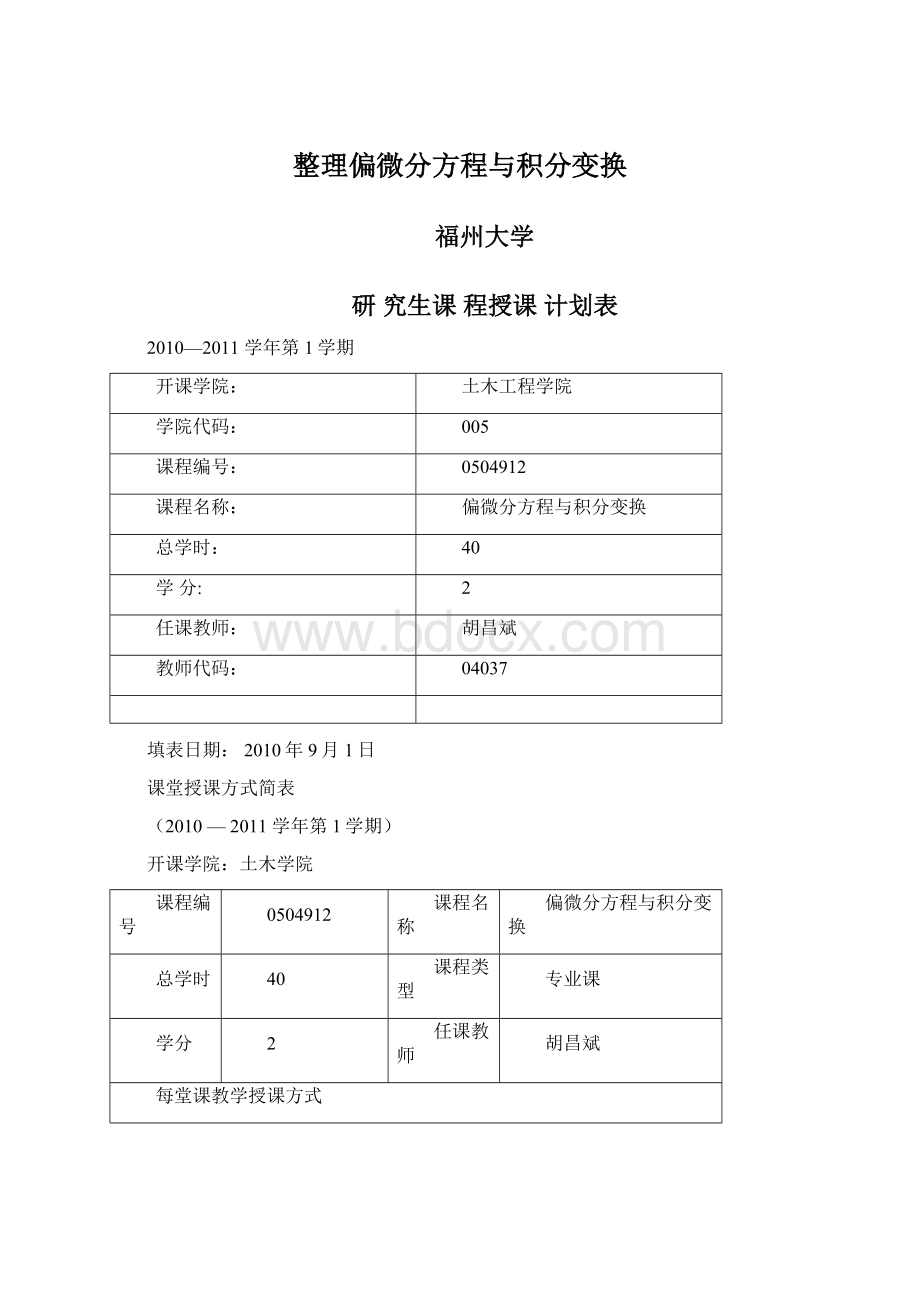
课程名称

总学时

课程类型

专业课

学分

任课教师

每堂课教学授课方式

讲课序数

周次

学时

授课方式

1

3

课堂讲授

11

12

13

4

14

复习备考

5

6

7

8

9

10

填表说明：

1、讲课序数指本堂课为本课程的第几次授课，单位时间（上午或下午或晚上）内的教学算

次讲课”；

2、授课方式填写：

①课堂讲授；

②课堂讨论；

③实验、上机；

④复习备考;

、课程类型填写：

学位课或非学位课。

4、总学时包括考试2〜3学时，复习备考的学时不能超过一次讲课学时数。

5、本表应根据校历填写，注意扣除国家法定假日和校运动会时间。

研究生课程授课计划表

教学目的

和要求

本课程研究内容由“数学物理方程”、“特殊函数”、和“积分变换”三大部分组成，

“数理方程”部分，主要介绍数学物理方程的一些基本概念及三种典型的二阶线性偏微分方程各种定结问题的一些常用解法，其中包括分离变量法、行波法、积分变换法、

格林函数法及差分法。

重点放在分离变量法上，较详细地讨论了三种典型方程在直角坐标系、极坐标系、柱坐标系与球坐标系中进行分离变量的一般步骤及各种边界条件的处理。

“特殊函数”部分，主要介绍贝赛尔函数及勒让德多项式，其中包括如何从求解数

学无理方程的定解问题引出贝赛尔方程与勒让德方程；

两个方程通解的表达式；

贝赛尔

方程与勒让德多项式的一些重要性质以及利用这两种特殊函数来解决数学物理方程的一些定解问题的全过程。

“积分变换”共分三部分，第一部分是傅立叶变化；

第二部分拉普拉斯变换；

第三

部分是积分变换的应用。

教学目的：

通过课程教学，应使学生掌握以上三部分的重要基本理论、分析方法和基于以上基本理论和方法解决实际科研问题的能力。

教学方法和手段

教学方法；

讲课为主，对教材中难点，不易理解之处，详细讲解，并适当添加图例解释。

教学手段：

通过课堂讲授并结合作业理解教学内容，增长科研才干的效果。

考试或考核

方式及要求

考核方式：

学生成绩的评定主要以期末考试成绩以及平时考勤为主。

本学期教学

新增内容

无

教材和主要

教学参考

资料

1、积分变换祝同江编高等教育出版社1995

2、数学物理方程与特殊函数南京工学院数学教研组编高等教育出版社1995

3、常微分方程王高雄高等学校教材高等教育出版社1983

任课教师签字

学位点负责人签字

早节

1、一些典型方程和定解条件的推导

学时数

起止周序

第1周

知

识

点

八、、

第一章一些典型方程和定解条件的推导

1.1基本方程的建立

1.2初始条件与边界条件

1.3定解问题的提法

培养能力

、.业L,、、八川厶十e、m厶厶厶1

培养学生建_

立数学物理方程的能力

本早

（节）对学生的要求

掌握一些典型方程和定解条件的推导，基本方程的建立，初始条件与边界条件，定解问题的提法

注：

每章填写一页，不够可另加页。

2、分离变量法

第2周

第二章分离变量法

2.1有界弦的自由振动

2.2有限长杆上的热传导

2.3圆域内的二维拉普拉斯方程的定解问题

掌握分离变量法，有界弦的自由振动，有限长杆上的热传导，圆域内的二维拉普拉斯方程的定解问题，等数学基本理论和基于这些基本理论进行科研问题分析的能力。

本

早

（节）

对

掌握分离变量法，有界弦的自由振动，有限长杆上的热传导，圆域内的二维拉普拉斯

学

方程的定解问题

生

的

要求

第3周

2.4非齐次方程的解法

2.5非齐次边界条件的处理

2.6关于二阶常微分方程固有值问题的一些结论

掌握非齐次方程的解法，非齐次边界条件的处理，关于二阶常微分方程固有值问题的一些结论，等数学基本理论和基于这些基本理论进行科研冋题分析的能力。

掌握非齐次方程的解法，非齐次边界条件的处理，关于二阶常微分方程固有值问题的一些结论

3、行波法与积分变换法

第4,5周

第三章

第四章行波法与积分变换法

3.1

3.2一维波动方程的达朗倍尔公式

3.3三维波动方程的泊松公式

3.3.1三维波动方程的球对称解

3.3.2三维波动方程的泊松公式

3.3.3泊松公式的物理意义

3.4积分变换法举例

掌握行波法与积分变换法，一维波动方程的达朗倍尔公式，三维波动方程的泊松公式，三维波动方程的球对称解，三维波动方程的泊松公式，泊松公式的物理意义，等数学基本理论和基于这些基本理论进行科研冋题分析的能力。

掌握行波法与积分变换法，一维波动方程的达朗倍尔公式，三维波动方程的泊松公式，三维波动方程的球对称解，三维波动方程的泊松公式，泊松公式的物理意义

4、拉普拉斯方程的格林函数法

6起止周序第6、7周

第五章拉普拉斯方程的格林函数法

4.1拉普拉斯方程边值问题的提法

4.2格林公式

4.3格林函数

4.4两种特殊区域的格林函数及狄氏问题的解

4.4.1半空间的格林函数

4.4.2球域的格林函数

掌握拉普拉斯方程的格林函数法，拉普拉斯方程边值问题的提法，格林公式，格林函数，两种特殊区域的格林函数及狄氏问题的解，半空间的格林函数，球域的格林函数，等数学基本理论和基于这些基本理论进行科研冋题分析的能力。

掌握拉普拉斯方程的格林函数法，拉普拉斯方程边值问题的提法，格林公式，格林函数，两种特殊区域的格林函数及狄氏问题的解，半空间的格林函数，球域的格林函数

5、贝塞尔函数

6起止周序第89周

第六章贝塞尔函数

5.1贝塞尔方程的引出

5.2贝塞尔方程的求解

5.3当n为整数时贝塞尔方程的通解

5.4贝塞尔函数的递推公式

5.5函数展成贝塞尔函数的级数

5.5.1贝塞尔函数的零点

5.5.2贝塞尔函数的正交性

5.6贝塞尔函数应用举例

5.7贝塞尔函数的其他类型

5.7.1第三类贝塞尔函数

5.7.2虚宗量的贝塞尔函数

5.7.3开尔文函数

5.8贝塞尔函数的渐近公式

掌握贝塞尔方程及其求解，当n为整数时贝塞尔方程的通解，贝塞尔函数的递推公式，

函数展成贝塞尔函数的级数，贝塞尔函数的零点，贝塞尔函数的正交性，贝塞尔函数应用，贝塞尔函数的其他类型，第三类贝塞尔函数，虚宗量的贝塞尔函数，开尔文函数，贝塞尔函数的渐近公式，等数学基本理论和基于这些基本理论进行科研问题分析的能力。

函数展成贝塞尔函数的级数，贝塞尔函数的零点，贝塞尔函数的正交性，贝塞尔函数应用，贝塞尔函数的其他类型，第三类贝塞尔函数，虚宗量的贝塞尔函数，开尔文函数，贝塞尔函数的渐近公式。

6、勒让德多项式

7、数学物理方程的差分解法

3起止周序第10周

第七章勒让德多项式

6.1勒让德方程的引出

6.2勒让德方程的求解

6.3勒让德多项式

6.4函数展成勒让德多项式的级数

6.4.1勒让德多项式的正交性

6.4.2函数展成勒让德多项式的级数

6.5连带的勒让德多项式第八章数学物理方程的差分解法

7.1将微分方程化成差分方程

7.2拉普拉斯方程的差分解法

7.3热传导方程的差分格式

7.4波动方程的差分格式

掌握勒让德多项式勒让德方程及求解，勒让德多项式，函数展成勒让德多项式的级数，勒让德多项式的正交性，函数展成勒让德多项式的级数，连带的勒让德多项式；

掌握数学物理方程的差分解法，等数学基本理论和基于这些基本理论进行科研问题分析的能力。

掌握数学物理方程的差分解法。

8、Fourier变换

第11周

第八章Fourier变换

1-1Fourier积分和Fourier变换的概念

一、主值意义下的广义积分

二、Fourier积分定理和Fourier变换的概念

1-2Fourier变换的性质

一、线性性质

二、位移性质

三、微分性质

四、积分性质

1-3单位脉冲函数及其Fourier变换

一、6-型序列和5-函数

二、构成6-型序列的充分条件

三、6-函数的积分

四、6-函数的Fourier变换

掌握Fourier积分和Fourier变换的概念，主值意义下的广义积分，Fourier积分定理和

Fourier变换的概念，Fourier变换的性质，线性性质，位移性质，微分性质，积分性质。

掌握单位脉冲函数及其Fourier变换，6-型序列和6-函数，构成6-型序列的充分条件，"

函数的积分，6-函数的Fourier变换，等数学基本理论和基于这些基本理论进行科研问题分析的能力。

掌握单位脉冲函数及其Fourier变换，6-型序列和6-函数，构成6-型序列的充分条件，6-函数的积分，5-函数的Fourier变换。

9、Laplace变换

第12周

第九章Laplace变换

2-1Laplace变换及其逆变换的概念

一、概念

一、Laplace变换存在定理

三、Laplace变换的线性性质

2-2Laplace逆变换的计算

2-3Laplace变换的性质（续）

一、微分性质

二、积分性质

三、位移性质

四、延迟性质时域上的位移性质

五、初值定理和终值定理

2-4常微分方程的Laplace变换解法

掌握Laplace变换及其逆变换的概念，Laplace变换存在定理，Laplace变换的线性性质，Laplace逆变换的计算，Laplace变换的性质，微分性质，积分性质，位移性质，延迟性质一一时域上的位移性质，初值定理和终值定理，常微分方程的Laplace变换解法，等

数学基本理论和基于这些基本理论进行科研问题分析的能力。

掌握Laplace变换及其逆变换的概念，Laplace变换存在定理，Laplace变换的线性性质，Laplace逆变换的计算，Laplace变换的性质，微分性质，积分性质，位移性质，延迟性质一一时域上的位移性质，初值定理和终值定理，常微分方程的Laplace变换解法。

10、积分变换的应用

第13周

第十章积分变换的应用

3-1卷积和卷积定理

一、卷积的概念

一、Fourier变换变换的卷积疋理

二、Laplace变换的卷积疋理

四、Fourier变换变换中的乘积疋理和能量积分

3-2Fourier变换在频域分析中的应用一一相关函数和非周期函数的频谱

一、相关函数和能量谱密度

二、非周期函数的频谱

3-3用积分变换解数学物理方程

一、用Fourier变换解某些数学物理方程

二、用Laplace变换解某些数学物理方程

掌握积分变换的应用，卷积和卷积定理，卷积的概念，Fourier变换变换的卷积定理，

Laplace变换的卷积疋理，Fourier变换变换中的乘积疋理和能量积分，Fourier变换在频

域分析中的应用一一相关函数和非周期函数的频谱，相关函数和能量谱密度，非周期函数的频谱，用积分变换解数学物理方程，用Fourier变换解某些数学物理方程，用

Laplace变换解某些数学物理方程，等数学基本理论和基于这些基本理论进行科研问题分析的能力。

Laplace变换解某些数学物理方程。

答疑与总复习

第14周