反比例函数基础测试题含答案文档格式.docx

反比例函数基础测试题含答案文档格式.docx

《反比例函数基础测试题含答案文档格式.docx》由会员分享，可在线阅读，更多相关《反比例函数基础测试题含答案文档格式.docx（26页珍藏版）》请在冰豆网上搜索。

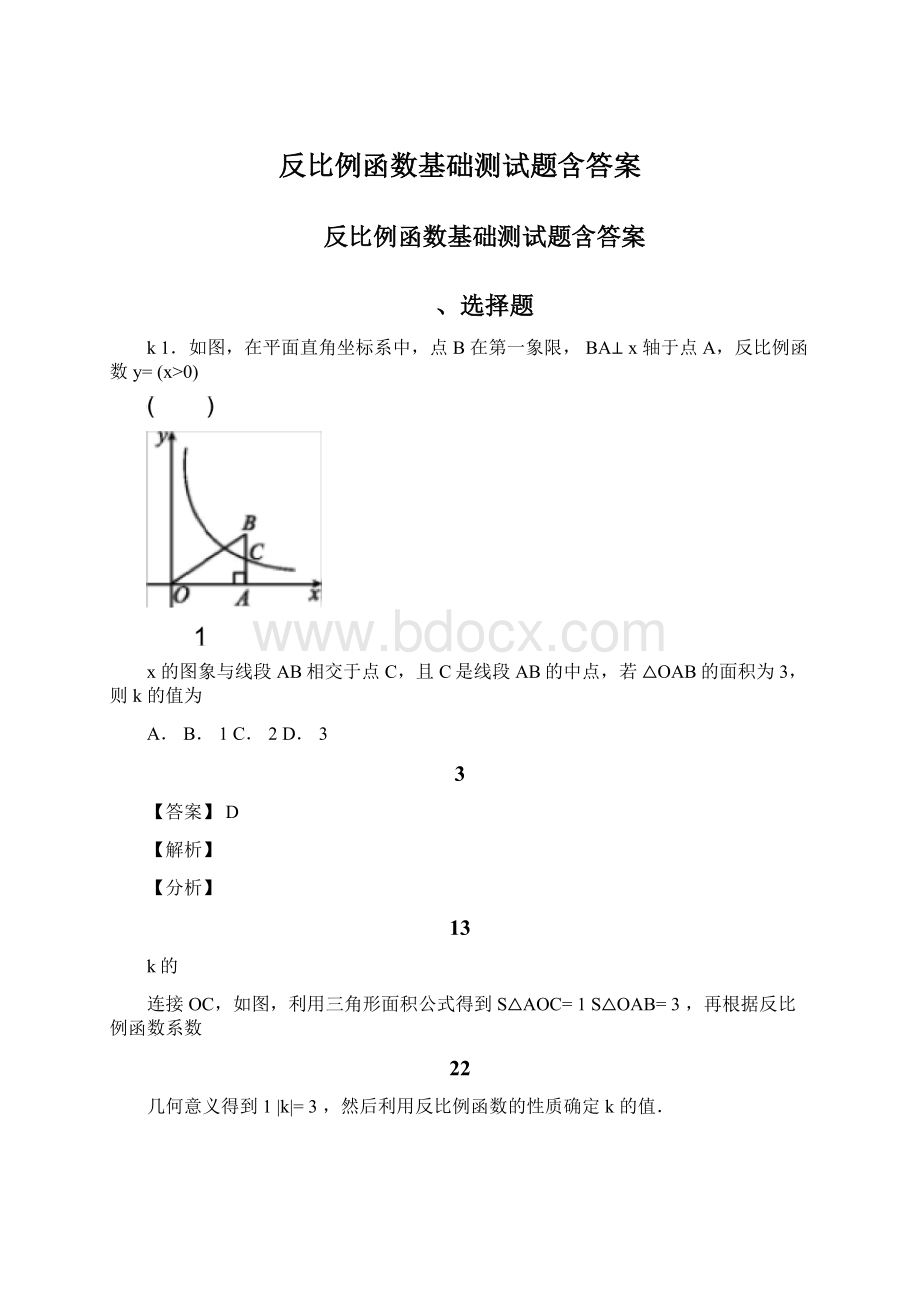
y3

根据k>

0，在图象的每一支上，y随x的增大而减小，双曲线在第一三象限，逐一分析即可．

4

∵反比例函数y=中的k=4>

∴在图象的每一支上，y随x的增大而减小，双曲线在第一三象限，

∵-2<

a<

0，

∴0>

y1>

y2，∵C（3，y3）在第一象限，

∴y3>

∴y2y1y3，

故选D．

【点睛】本题考查了反比例函数的性质，熟练地应用反比例函数的性质是解题的关键．

3．ABC的面积为2，边BC的长为x，边BC上的高为y，则y与x的变化规律用图象表示大致是（）

B．

A．

C．

D．

答案】A

根据三角形面积公式得出y与x的函数解析式，根据解析式作出图象进行判断即可．

根据题意得

1xy2

∴y

∵x0，y0

∴y与x的变化规律用图象表示大致是

故答案为：

A．

【点睛】本题考查了反比例函数的图象问题，掌握反比例函数图象的性质是解题的关键．

k

4．如图，点A是反比例函数y＝（x<

0）的图象上的一点，过点A作平行四边形

ABCD，使点B、C在x轴上，点D在y轴上．已知平行四边形ABCD的面积为8，则k的值为（）

A．8B．﹣8C．4D．﹣4

【答案】B

作AE⊥BC于E，由四边形ABCD为平行四边形得AD∥x轴，则可判断四边形ADOE为矩形，所以S平行四边形ABCD=S矩形ADOE，根据反比例函数k的几何意义得到S矩形ADOE=|k|．【详解】

解：

作AE⊥BC于E，如图，

∵四边形ABCD为平行四边形，

∴AD∥x轴，

∴四边形ADOE为矩形，

∴S平行四边形ABCD=S矩形ADOE，

而S矩形ADOE=|k|，

∴|k|=8，

而k<

0

∴k=-8．

故选：

B．

【点睛】

kk

本题考查了反比例函数y=（k≠0）系数k的几何意义：

从反比例函数y=（k≠0）图象

xx上任意一点向x轴和y轴作垂线，垂线与坐标轴所围成的矩形面积为|k|．

P作PMx轴，垂

5．如图，点P是反比例函数y（k0）的图象上任意一点，过点x

解析】

分析】

k的几何意义得到1|k|=2

定k的值．

∵△POM的面积等于2.5，

∴12|k|=2.5，而k<

∴k=-5，故选：

本题考查了反比例函数系数k的几何意义：

在反比例函数y=图象中任取一点，过这一个

点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．也考查了反比例函数的性质．

6．对于反比例函数y，下列说法不正确的是（）

A．点（﹣2，﹣1）在它的图象上B．它的图象在第一、三象限

C．当x>

0时，y随x的增大而增大D．当x<

0时，y随x的增大而减小

【答案】C

【详解】由题意分析可知，一个点在函数图像上则代入该点必定满足该函数解析式，点（-2，-1）

代入可得，x=-2时，y=-1，所以该点在函数图象上，A正确；

因为2大于0所以该函数图象在第一，三象限，所以B正确；

C中，因为2大于0，所以该函数在x>

0时，y随x的增大而减小，所以C错误；

D中，当x<

0时，y随x的增大而减小，正确，故选C.

考点：

反比例函数

【点睛】本题属于对反比例函数的基本性质以及反比例函数的在各个象限单调性的变化

35

7．给出下列函数：

①y＝﹣3x+2：

②y＝；

③y＝﹣：

④y＝3x，上述函数中符合条xx

件“当x>

1时，函数值y随自变量x增大而增大”的是（）

A．①③B．③④C．②④D．②③

【分析】分别利用一次函数、正比例函数、反比例函数的增减性分析得出答案．

①y＝﹣3x+2，当x>

1时，函数值y随自变量x增大而减小，故此选项不符合题意；

2y＝，当x>

5

3y＝﹣，当x>

1时，函数值y随自变量x增大而增大，故此选项符合题意；

4y＝3x，当x>

1时，函数值y随自变量x增大而增大，故此选项符合题意；

故选：

【点睛】此题考查一次函数、正比例函数、反比例函数，正确把握相关性质是解题关键．

8．若一个圆锥侧面展开图的圆心角是270°

，圆锥母线l与底面半径r之间的函数关系图象

【分析】根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于

270l4

圆锥的母线长得到2πr=，整理得l=r（r>

0），然后根据正比例函数图象求

1803

解．

根据题意得2πr=270l，所以l=4r（r>

0），

即l与r为正比例函数关系，其图象在第一象限．

故选A．

【点睛】本题考查圆锥的计算；

函数的图象．

9．如图，直线l与x轴、y轴分别交于A、B两点，与反比例函数y＝的图象在第一象限x

∴OA＝

【点睛】本题考查直线和反比例函数的交点问题，待定系数法求函数解析式，会运用相似求线段长度是解题的关键．

10．如图，在x轴的上方，直角∠BOA绕原点O按顺时针方向旋转.若∠BOA的两边分别与

12

函数y、y的图象交于B、A两点，则∠OAB大小的变化趋势为（）

xx

可代入比例式求得

∴∠OAB大小是一个定值，因此∠OAB的大小保持不变故选D

y轴

该题主要考查了反比例函数图象上点的坐标特征、相似三角形的判定等知识点及其应用问题；

解题的方法是作辅助线，将分散的条件集中；

解题的关键是灵活运用相似三角形的判定等知识点来分析、判断、推理或解答．

11．如图，在平面直角坐标系中，等腰直角三角形ABC的顶点A、B分别在x轴、

的正半轴上，ABC90，CAx轴，点C在函数yx0的图象上，若x

解析】分析】

根据题意可以求得OA和AC的长，从而可以求得点C的坐标，进而求得k的值，本题得以解决．

⊥x轴，AB1，

BAC

BAO45，

OAOB

点C的坐标为,2，

Q点C在函数yx0的图象上，

k221，

A．

【点睛】本题考查反比例函数图象上点的坐标特征、等腰直角三角形，解答本题的关键是明确题意，利用数形结合的思想解答．

12．如图，Rt△AOB中，∠AOB=90°

，AO=3BO，OB在x轴上，将Rt△AOB绕点O顺时针旋2k

转至△RtA'

OB'

，其中点B'

落在反比例函数y=﹣的图象上，OA'

交反比例函数y=的图象

A．4

答案】C

7

C．8

D．7

设将Rt△AOB绕点O顺时针旋转至由题意可得，点B′的坐标为（acosα，

Rt△A'

的旋转角为α，OB=a，则OA=3a，

﹣asinα），点C的坐标为（2asinα，2acosα），

∵点B'

在反比例函数y=﹣的图象上，

﹣asinα﹣=，得a2sinαcosα，=2

acosα

又∵点C在反比例函数y=的图象上，

∴2acosα=，得k=4a2sin

2asinα

αcosα=8.

故选C.

【点睛】本题主要考查反比例函数与几何图形的综合问题，解此题的关键在于先设旋转角为α，利用旋转的性质和三角函数设出点B'

与点C的坐标，再通过反比例函数的性质求解即可.

13．如图，已知在平面直角坐标系中，点O是坐标原点，VAOB是直角三角形，

AOB90，OB

2OA，点B在反比例函数y2上，若点A在反比例函数y

答案】B

通过添加辅助线构造出相似三角形，再根据相似三角形的性质可求得

1x

，然后由

x2

点的坐标即可求得答案．

过点B作BE⊥x于点E，过点A作AFx于点F，如图：

∵点B在反比例函数y2上

∴设Bx,2

∴OEx，BE2

AOB

90

AOD

BOD

BOE

AOF

BE⊥x，

AFx

BEO

OFA

OAF

∴VBOE∽VOAF

OB

2OA

OF

AF

OA

BE

OE

BO

11

，AF

2x

∵点A在反比例函数y上

x∴2

∴k

14．当x0时，反比例函数y2的图象（）

A．在第一象限，

y随x的增大而减小

B．在第二象限，

y随x的增大而增大

C．在第三象限，

y随x的增大而减小

D．在第四象限，

点在函数图象上则点的坐标就满足函数

A的坐标是解决问题的关键．

本题考查了反比例函数与相似三角形的综合应用，解析式，结合已知条件能根据相似三角形的性质求得点

反比例函数y中的k20，图像分布在第二、四象限；

利用x0判断即可．

Q反比例函数y中的k20，

该反比例函数的图像分布在第二、四象限；

又Qx0，

图象在第二象限且y随x的增大而增大．

B．

k本题主要考查的是反比例函数的性质，对于反比例函数yk0，

（1）k0，反比x例函数图像分布在一、三象限；

（2）k0，反比例函数图像分布在第二、四象限内．

15．反比例函数y=的图象如图所示，则一次函数y=kx+b（k≠）0的图象的图象大致是

分析】先由反比例函数的图象得到k，b同号，然后分析各选项一次函数的图象即可

∵y=的图象经过第一、三象限，∴kb>

∴k，b同号，选项A图象过二、四象限，则故此选项不合题意；

选项B图象过二、四象限，则项不合题意；

选项C图象过一、三象限，则故此选项不合题意；

选项D图象过一、三象限，则k>

0，图象经过y轴正半轴，则b>

0，此时，k，b同号，故此选项符合题意；

故选D．考点：

反比例函数的图象；

一次函数的图象．

k<

k>

图象经过y轴正半轴，则b>

0，此时，k，b异号，

图象经过原点，则b=0，此时，k，b不同号，故此选

图象经过y轴负半轴，则b<

16．如图，△AOB是直角三角形，∠AOB＝90°

，△AOB的两边分别与函数y1,y2的

图象交于B、A两点，则等于（

A．2

【答案】A

过点A,B作AC⊥x轴,BD⊥x轴,垂足分别为C,D.根据条件得到△ACO∽△ODB.根据反比例函

D．3

数比例系数

k的几何意义得出SOBD（OB

SAOCOA

）2＝2＝1利用相似三角形面积比等于相似比

的平方得出

OB2

OA2

∵∠AOB＝90°

，

∴∠AOC+∠BOD＝∠AOC+∠CAO＝90°

，∠CAO＝∠BOD，

∴△ACO∽△BDO，

SOBD（OB）2,

SAOC（OA）,

111

∵S△AOC＝×

＝21，S△BOD＝×

1＝，

222

此题考查了反比例函数图象上点的坐标特征和相似三角形的判定与性质，解题关键在于做辅助线，然后得到相似三角形再进行求解

17．如图，矩形ABCD的顶点A，B在x轴的正半轴上，反比例函数

A．1

解析】【分析】

设OA为4a，则根据题干中的比例关系，可得AD=3a，CE=2a，BE=a，从而得出点D和点E

的坐标（用a表示），代入反比例函数可求得a的值，进而得出BC长.

【详解】设OA=4a

根据CE2，AD3得：

AD=3a，CE=2a，BE=a

BEOA4

∴D（4a，3a），E（4a+4，a）将这两点代入解析得；

4a4

解得：

a=

∴BC=AD=

B

本题考查反比例函数和矩形的性质，解题关键是用含有字母的式子表示出点D、E的坐

标，然后代入解析式求解.

18．已知点（x1,y1），

（x2,y2）均在双曲线y

1x上，

下列说法中错误的是（）

A．若x1

x2，则y1

y2

若x1

C．若0

x1x2，则

y1y2

x20，则y1

【答案】

D

先把点A

（x1，y1）、

B（x2，y2）代入双曲线

y

用y1、y2表示出

x1，x2，据此进行

判断．

1∵点（x1，y1），（x2，y2）均在双曲线y上，

∴y1，y2．

x1x2

A、当x1=x2时，-=-，即y1=y2，故本选项说法正确；

B、当x1=-x2时，-=，即y1=-y2，故本选项说法正确；

C、因为双曲线y位于第二、四象限，且在每一象限内，y随x的增大而增大，所以x

当0<

x1<

x2时，y1<

y2，故本选项说法正确；

D、因为双曲线y位于第二、四象限，且在每一象限内，y随x的增大而增大，所以

当x1<

x2<

0时，y1>

y2，故本选项说法错误；

【点睛】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键．

19．如图，A、C是函数y1的图象上任意两点，过点A作y轴的垂线，垂足为B，过点x

C作y轴的垂线，垂足为D．记RtAOB的面积为S1，RtCOD的面积为S2，则S1和S2

C．S1=S2D．由A、C两点的位置确定

根据双曲线的图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角

形面积S的关系即S=1k|．

11由题意得：

S1=S2=|k|=．

22故选：

C．

本题主要考查了反比例函数y＝k中k的几何意义，即图象上的点与原点所连的线段、坐

1标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=|k|，是经常考查的一个

知识点；

这里体现了数形结合的思想．

20．在反比例函数

y＝9m3图象上有两点A（x1，y1）、B（x2，y2），y1<

0<

y2，x1>

x2，则有

m的取值范围即

先根据y1<

y2，有x1>

x2，判断出反比例函数的比例系数的正负，求出可．

详解】

B（x2，y2），y1<

x2，

∵在反比例函数y＝9m3图象上有两点A（x1，y1）x

∴反比例函数的图象在二、四象限，

∴9m+3<

0，解得m<

﹣．

此题主要考查了反比例函数的性质，以及反比例函数图象上点的坐标特点，关键是掌握反比例函数的性质