潮流计算报告Word格式文档下载.docx

潮流计算报告Word格式文档下载.docx

《潮流计算报告Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《潮流计算报告Word格式文档下载.docx（28页珍藏版）》请在冰豆网上搜索。

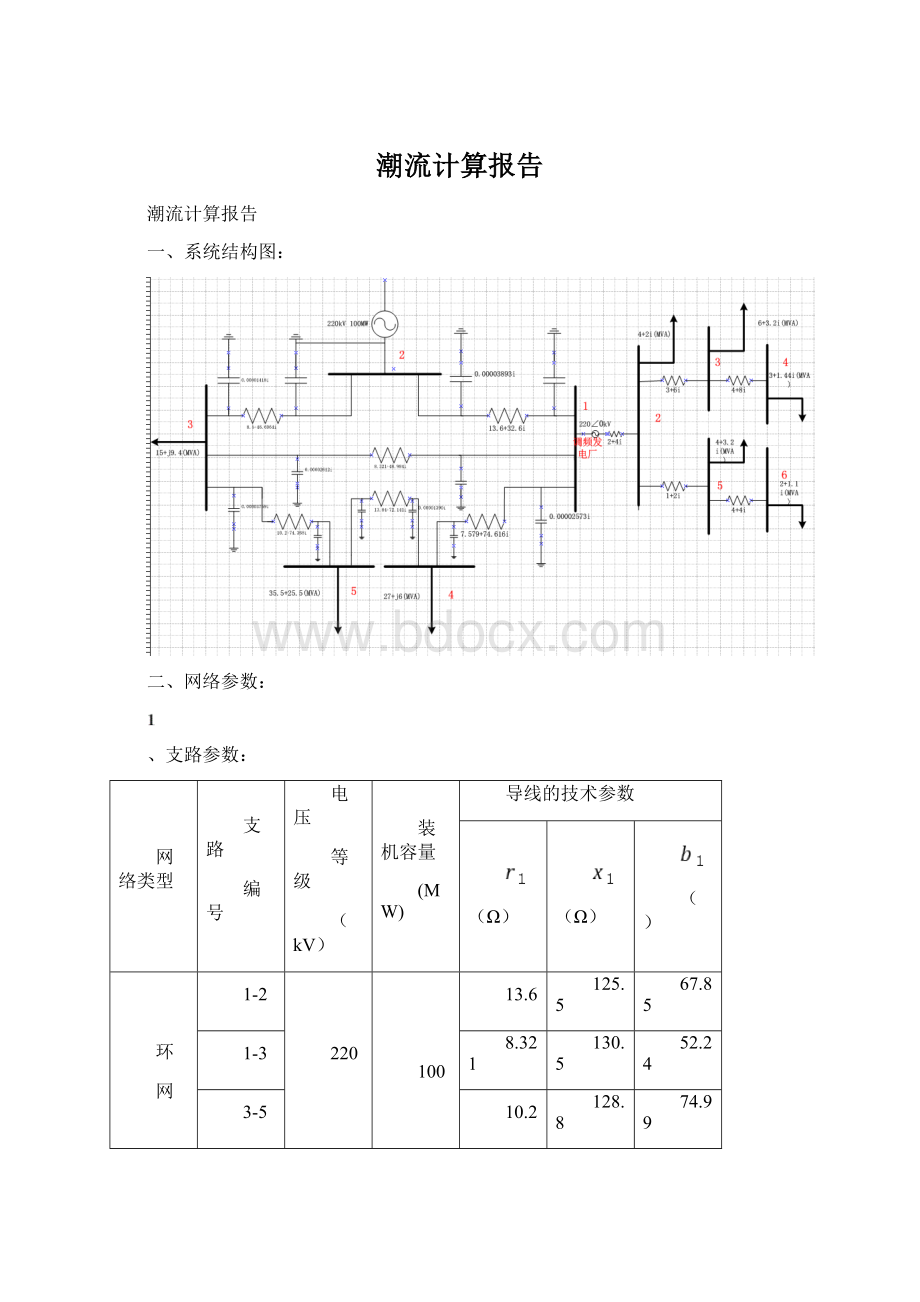
3

6

3-4

8

2-5

1

5-6

2、节点参数：

节点类型

节点编号

发电功率（MW）

负荷视在功率

未知（平衡节点）

0（PV节点）

15+9.4i

27+6i

5

35.5+25.5i

4+2i

6+3.2i

3+1.44i

4+3.2i

2+1.1i

三、潮流计算流程图:

四、matlab程序：

clear;

Un=input（'

请输入Un:

'

）;

%输入所需的额定电压

PQ=[

%节点电压有功无功

Un00

Un42

Un63.2

Un31.44

Un43.2

Un21.1

];

FT=[

%首端末端

43

32

65

52

21

RX=[

%RX

48

36

44

12

24

NN=size（PQ,1）;

%节点数

NB=size（FT,1）;

%支路数数

V=PQ（:

1）;

%V初始电压相量

maxd=1

k=1

whilemaxd>

0.0001

k=k+1;

PQ2=PQ;

%每一次迭代各节点的注入有功和无功相同

PL=0.0;

fori=1:

NB

kf=FT（i,1）;

%前推始节点号

kt=FT（i,2）;

%前推终节点号

x=（PQ2（kf,2）^2+PQ2（kf,3）^2）/V（kf）/V（kf）;

%计算沿线电流/平方A

losss（i,1）=RX（i,1）*x;

%计算线路有功损耗/MW

losss（i,2）=RX（i,2）*x;

%计算线路无功损耗/MW

PQ1（i,1）=PQ2（kf,2）+RX（i,1）*x;

%计算支路首端有功/MWRX（i,1）*R

PQ1（i,2）=PQ2（kf,3）+RX（i,2）*x;

%计算沿支路的无功/MWRX（i,2）*X

PQ2（kt,2）=PQ2（kt,2）+PQ1（i,1）;

%用PQ1去修正支路末端节点的有功P单位MW

PQ2（kt,3）=PQ2（kt,3）+PQ1（i,2）;

%用PQ1去修正支路末端节点的有功Q单位Mvar

end

angle

（1）=0.0;

fori=NB:

-1:

kf=FT（i,2）;

%回代始节点号

kt=FT（i,1）;

%回代终节点号

dv1=（PQ1（i,1）*RX（i,1）+PQ1（i,2）*RX（i,2））/V（kf）;

%计算支路电压损耗的纵分量dv1

dv2=（PQ1（i,1）*RX（i,2）-PQ1（i,2）*RX（i,1））/V（kf）;

%计算支路电压损耗的横分量dv2

V2（kt）=sqrt（（V（kf）-dv1）^2+dv2^2）;

%计算支路末端电压/kV

angle（kt）=angle（kf）+atand（dv2/（V（kf）-dv1））;

%计算支路

maxd=abs（V2

（2）-V

（2））;

V2

（1）=V

（1）;

fori=3:

1:

NN

ifabs（V2（i）-V（i））>

maxd;

maxd=abs（V2（i）-V（i））;

end

fullloss（1,1）=0;

%计算线路总损耗

fullloss（1,2）=0;

finalPQ=max（PQ1）;

fori=1:

fullloss（1,1）=fullloss（1,1）+losss（i,1）;

fullloss（1,2）=fullloss（1,2）+losss（i,2）;

end

disp（'

辐射网迭代次数：

）

k

辐射网系统电压差精度：

）

maxd

辐射网系统末端节点有功和无功：

finalPQ%潮流分布即支路首端潮流MVA

辐射网系统总功率损耗：

fullloss%线路总损耗MVA

辐射网系统各支路功率损耗：

losss%各支路损耗MVA

辐射网系统各节点电压幅值：

V=V2%节点电压模计算结果kV

辐射网系统各节点电压相角：

angle%节点电压角度计算结果单位度

clc

辐射网系统末端节点有功和无功/MVA：

FinPQ=finalPQ（1,1）+finalPQ（1,2）*j%潮流分布即支路首端潮流MVA

辐射网系统总功率损耗/MVA：

Fulloss=fullloss（1,1）+fullloss（1,2）*j%线路总损耗MVA

辐射网系统各支路功率损耗/MVA：

for（a=1:

5）

LOSS=losss（a,1）+losss（a,2）*j%各支路损耗MVA

辐射网系统各节点电压幅值/KV：

n=5;

%input（'

节点数'

nl=6;

支路数'

isb=1;

平衡母线节点号'

pr=0.000001;

误差精度：

pr='

B1=[1,2,13.6+125.5i,0.00006785i,1,0;

1,3,8.321+130.5i,0.00005224i,1,0;

3,5,10.2+128.8i,0.00007499i,1,0;

2,3,8.5+105.4i,0.00002836i,1,0;

1,4,7.579+129.6i,0.00005145i,1,0;

4,5,13.84+125.31i,0.0000278i,1,0];

由支路参数形成的矩阵'

B2=[-FinPQ,0,Un,0,0,1;

100,0,Un,Un,0,3;

0,15+9.4i,Un,0,0,2;

0,27+6i,Un,0,0,2;

0,35.5+25.5i,Un,0,0,2];

各节点参数形成的矩阵'

Y=zeros（n）;

e=zeros（1,n）;

f=zeros（1,n）;

V=zeros（1,n）;

sida=zeros（1,n）;

S1=zeros（nl）;

%对各矩阵置零

%－－－－－－－修改部分－－－－－－－－－－－－

ym=1;

SB=100;

UB=Un;

%定义视在功率和电压基值

ifym~=0%若不是标幺值

YB=SB./UB./UB;

%定义导纳标幺值

BB1=B1;

BB2=B2;

nl

B1（i,3）=B1（i,3）*YB;

%切换为阻抗标幺值

B1（i,4）=B1（i,4）./YB;

%切换为导纳标幺值

disp（'

支路矩阵B1='

sparseB1=sparse（B1）;

disp（sparseB1）%输出标幺值稀疏矩阵B1

-----------------------------------------------------'

n

B2（i,1）=B2（i,1）./SB;

%切换为视在功率标幺值

B2（i,2）=B2（i,2）./SB;

B2（i,3）=B2（i,3）./UB;

%切换为电压标幺值

B2（i,4）=B2（i,4）./UB;

B2（i,5）=B2（i,5）./SB;

节点矩阵B2='

sparseB2=sparse（B2）;

disp（sparseB2）%输出标幺值稀疏矩阵B2

%%%---------------------------------------------------

nl%支路数

ifB1（i,6）==0%左节点处于1侧

p=B1（i,1）;

q=B1（i,2）;

else

p=B1（i,2）;

q=B1（i,1）;

%使左节点处于低压侧

Y（p,q）=Y（p,q）-1./（B1（i,3）*B1（i,5））;

%求解非对角元导纳

Y（q,p）=Y（p,q）;

%对角元两侧对称

Y（q,q）=Y（q,q）+1./（B1（i,3）*B1（i,5）^2）+B1（i,4）./2;

%对角元K侧

Y（p,p）=Y（p,p）+1./B1（i,3）+B1（i,4）./2;

%对角元1侧

%求导纳矩阵

导纳矩阵Y='

sparseY=sparse（Y）;

disp（sparseY）%输出导纳稀疏矩阵

%----------------------------------------------------------

G=real（Y）;

B=imag（Y）;

%分解出导纳阵的实部和虚部

n

e（i）=real（B2（i,3））;

%给定i节点初始电压的实部

f（i）=imag（B2（i,3））;

%给定i节点初始电压的虚部

V（i）=B2（i,4）;

%PV节点电压给定模值

n%给定各节点注入功率

S（i）=B2（i,1）-B2（i,2）;

%i节点注入功率SG-SL

B（i,i）=B（i,i）+B2（i,5）;

%i节点无功补偿量

%===================================================================

P=real（S）;

Q=imag（S）;

%定义有功功率和无功功率

ICT1=0;

IT2=1;

N0=2*n;

N=N0+1;

a=0;

%定义迭代次数ICT1和不满足精度要求的节点个数IT2

whileIT2~=0%仍有不满足精度要求的节点

IT2=0;

a=a+1;

%IT2置零

ifi~=isb%非平衡节点

C（i）=0;

D（i）=0;

forj1=1:

C（i）=C（i）+G（i,j1）*e（j1）-B（i,j1）*f（j1）;

%Σ（Gij*ej-Bij*fj）

D（i）=D（i）+G（i,j1）*f（j1）+B（i,j1）*e（j1）;

%Σ（Gij*fj+Bij*ej）

P1=C（i）*e（i）+f（i）*D（i）;

%节点功率P计算eiΣ（Gij*ej-Bij*fj）+fiΣ（Gij*fj+Bij*ej）

Q1=C（i）*f（i）-e（i）*D（i）;

%节点功率Q计算fiΣ（Gij*ej-Bij*fj）-eiΣ（Gij*fj+Bij*ej）

%求P'

Q'

V2=e（i）^2+f（i）^2;

%电压模平方

%=========以下针对非PV节点来求取功率差及Jacobi矩阵元素=========

ifB2（i,6）~=3%非PV节点

DP=P（i）-P1;

%节点有功功率差

DQ=Q（i）-Q1;

%节点无功功率差

%===============以上为除平衡节点外其它节点的功率计算=================

%=================求取Jacobi矩阵===================

ifj1~=isb&

j1~=i%非平衡节点&

非对角元

X1=-G（i,j1）*e（i）-B（i,j1）*f（i）;

%X1=N（i,j1）=dDP（i）/de（j1）

X2=B（i,j1）*e（i）-G（i,j1）*f（i）;

%X2=H（i,j1）=dDP（i）/df（j1）

X3=X2;

%X2=H（i,j1）=dDP（i）/df（j1）=X3=M（i,j1）=dDQ（i）/de（j1）

X4=-X1;

%X1=N（i,j1）=dDP（i）/de（j1）=-X4=-L（i,j1）=-dDQ（i）/df（j1）

p=2*i-1;

q=2*j1-1;

J（p,q）=X3;

J（p,N）=DQ;

m=p+1;

%扩展列△Q

J（m,q）=X1;

J（m,N）=DP;

q=q+1;

%扩展列△P

J（p,q）=X4;

J（m,q）=X2;

%对Jacobi矩阵赋值

elseifj1==i&

j1~=isb%非平衡节点&

对角元

X1=-C（i）-G（i,i）*e（i）-B（i,i）*f（i）;

%X1=N（i,i）=dDP（i）/de（i）

X2=-D（i）+B（i,i）*e（i）-G（i,i）*f（i）;

%X2=H（i,i）=dDP（i）/df（i）

X3=D（i）+B（i,i）*e（i）-G（i,i）*f（i）;

%X3=M（i,i）=dDQ（i）/de（i）

X4=-C（i）+G（i,i）*e（i）+B（i,i）*f（i）;

%X4=L（i,i）=dDQ（i）/df（i）

J（p,q）=X3;

m=p+1;

J（p,q）=X4;

J（m,q）=X2;

%===============下面是针对PV节点来求取Jacobi矩阵的元素===========

%PV节点有功误差

DV=V（i）^2-V2;

%PV节点电压误差

%X2=H（i,j1）=dDP（i）/df（j1）

X5=0;

X6=0;

%X5=R（i,j1）=X6=S（i,j1）=0

J（p,q）=X5;

J（p,N）=DV;

%扩展列△V

J（p,q）=X6;

X5=-2*e（i）;

%X5=R（i,i）=-2e（i）

X6=-2*f（i）;

%X6=F（i,i）=-2f（i）

%对Jacobi矩阵赋值

%=========以上为求雅可比矩阵的各个元素=====================

fork=3:

N0%N0=2*n（从第三行开始，第一、二行是平衡节点）

k1=k+1;

N1=N;

%N=N0+1即N=2*n+1扩展列△P、△Q

fork2=k1:

N1%扩展列△P、△Q

J（k,k2）=J（k,k2）./J（k,k）;

%非对角元规格化

J（k,k）=1;

%对角元规格化

ifk~=3%不是第三行

%============================================================

k4=k-1;

fork3=3:

k4%用k3行从第三行开始到当前行前的k4行消去

N1%k3行后各行下三角元素

J（k3,k2）=J（k3,k2）-J（k3,k）*J（k,k2）;

%消去运算

J（k3,k）=0;

ifk==N0

break;

%==========================================

fork3=k1:

N0

N1

%====上面是用线性变换方式将Jacobi矩阵化成单位矩阵（利用线性代数求解电压实部与虚部）=====

2:

N0-1

L=（k+1）./2;

e（L）=e（L）-J（k,N）;

%修改节点电压实部

f（L）=f（L）-J（k1,N）;

%修改节点电压虚部

%------修改节点电压-----------

DET=abs（J（k,N））;

ifDET>

=pr%电压偏差量是否满足要求

IT2=IT2+1;

%不满足要求的节点数加1

ICT2（a）=IT2;

ICT1=ICT1+1;

%用高斯消去法解"

w=-J*V"

迭代次数'

disp（ICT1）;

没有达到精度要求的个数'

disp（ICT2）;

fork=1:

V（k）=sqrt（e（k）^2+f（k）^2）;

%计算实际电压大小

sida（k）=atan（f（k）./e（k））*180./pi;

%计算实际电压相角

E（k）=e（k）+f（k）*j;

%计算实际电压相量

%===============计算各输出量===========================

各节点的实际电压标幺值E为（节点号从小到大排列）：

sparseE=sparse（E）;

disp（sparseE）;

EE=E*UB;

各节点的实际电压EE为（节点号从小到大排列）：

sparseEE=sparse（EE）;

disp（sparseEE）;

各节点的电压标幺值幅值V为（节点号从小到大排列）：

sparseV=sparse（V）;

disp（sparseV）;

VV=V*UB;

各节点的电压幅值VV为（节点号从小到大排列）：

sparseVV=sparse（VV）;

disp（sparseVV）;

各节点的电压相角为（节点号从小到大排列）：

sparsesida=sparse（sida）;

disp（sparsesida）

forp=1:

C（p）=0;

forq=1:

C（p）=C（p）+conj（Y（p,q））*conj（E（q））;

%计算电流的共轭

S（p）=E（p）*C（p）;

%计算节点的视在功率

各节点的功率标幺值S为（节点号从小到大排列）：

sparseS=sparse（S）;

disp（sparseS）;

各节点的功率实际值SS为（节点号从小到大排列）：

SS=S*SB;

sparseSS=sparse（SS）;

disp（sparseSS）;

各条支路的功率损耗S标幺值和实际值SS为（顺序支路参数矩阵顺序一致）：

HDDS=0;

Si（p,q）=E（p）*（conj（E（p））*conj（B1（i,4）./2）+（E（p）-E（q））*（conj（E（p））-conj（E（q）））*conj（1./（B1（i,3））））+E（q）*（conj（E（q））*conj（B1（i,4）./2））;

ZF1=['

S（'

num2str（p）,'

'

num2str（q）,'

）='

num2str（Si（p,q））];

disp（ZF1）;

SSi（p,q）=Si（p,q）*SB;

%计算