 梁模板计算书Word格式.docx
梁模板计算书Word格式.docx
- 文档编号:18476923
- 上传时间:2022-12-17
- 格式:DOCX
- 页数:15
- 大小:169.11KB
梁模板计算书Word格式.docx
《梁模板计算书Word格式.docx》由会员分享,可在线阅读,更多相关《梁模板计算书Word格式.docx(15页珍藏版)》请在冰豆网上搜索。
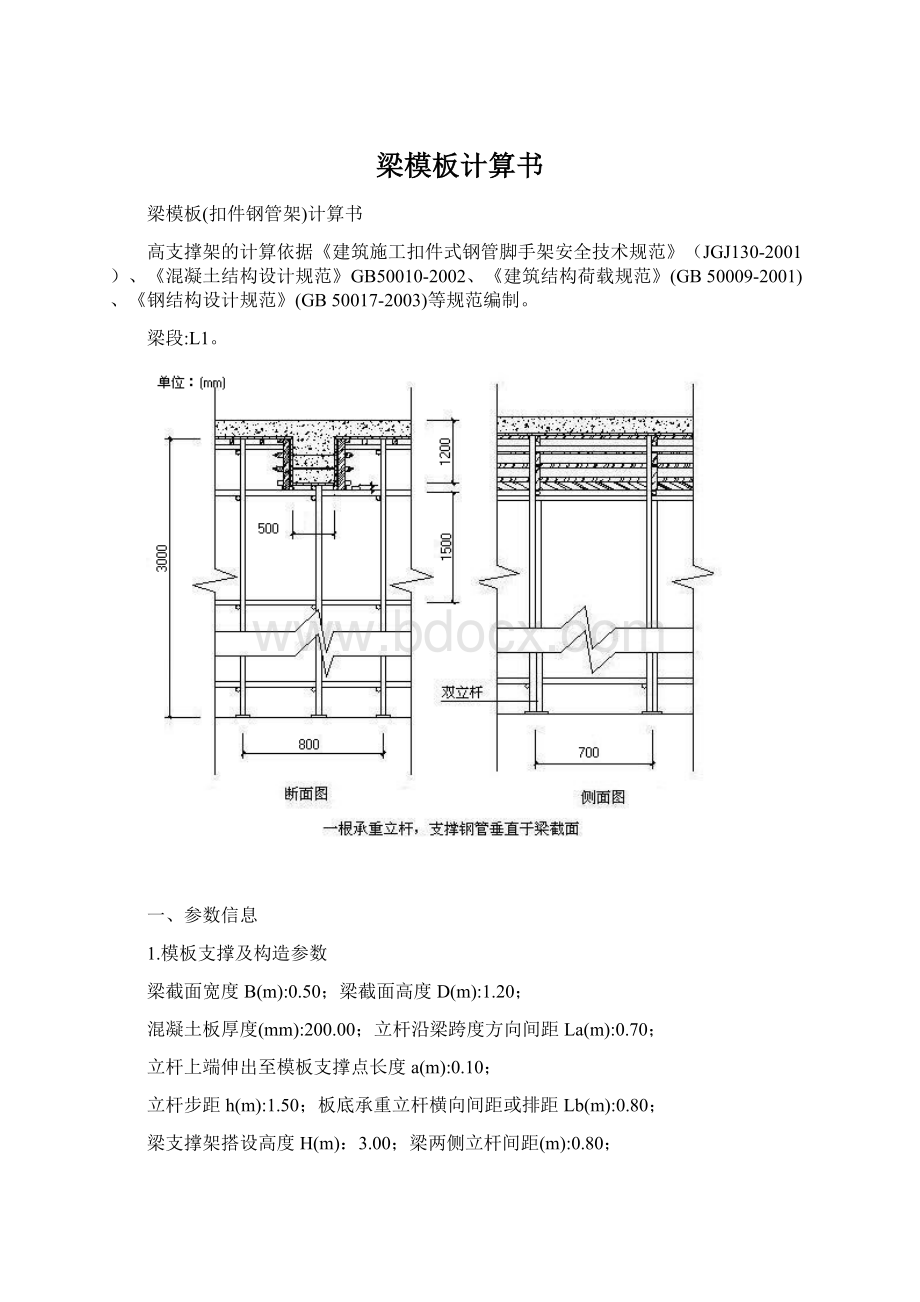
9000.0;
木材抗弯强度设计值fm(N/mm2):
13.0;
木材抗剪强度设计值fv(N/mm2):
1.5;
面板类型:
胶合面板;
面板弹性模量E(N/mm2):
9500.0;
面板抗弯强度设计值fm(N/mm2):
4.梁底模板参数
梁底纵向支撑根数:
面板厚度(mm):
14.0;
5.梁侧模板参数
次楞间距(mm):
250,主楞竖向根数:
4;
主楞间距为:
100mm,220mm,210mm;
穿梁螺栓水平间距(mm):
500;
穿梁螺栓直径(mm):
M14;
主楞龙骨材料:
钢楞;
截面类型为圆钢管48×
3.0;
主楞合并根数:
2;
次楞龙骨材料:
木楞,宽度50mm,高度100mm;
次楞合并根数:
二、梁模板荷载标准值计算
1.梁侧模板荷载
强度验算要考虑新浇混凝土侧压力和倾倒混凝土时产生的荷载;
挠度验算只考虑新浇混凝土侧压力。
其中γ--混凝土的重力密度,取24.000kN/m3;
t--新浇混凝土的初凝时间,可按现场实际值取,输入0时系统按200/(T+15)计算,得5.714h;
T--混凝土的入模温度,取20.000℃;
V--混凝土的浇筑速度,取1.500m/h;
H--混凝土侧压力计算位置处至新浇混凝土顶面总高度,取0.750m;
β1--外加剂影响修正系数,取1.200;
β2--混凝土坍落度影响修正系数,取1.150。
根据以上两个公式计算的新浇筑混凝土对模板的最大侧压力F;
分别计算得50.994kN/m2、18.000kN/m2,取较小值18.000kN/m2作为本工程计算荷载。
三、梁侧模板面板的计算
面板为受弯结构,需要验算其抗弯强度和刚度。
面板计算简图(单位:
mm)
1.强度计算
跨中弯矩计算公式如下:
其中,W--面板的净截面抵抗矩,W=100×
2.1×
2.1/6=73.5cm3;
M--面板的最大弯距(N·
mm);
σ--面板的弯曲应力计算值(N/mm2)
[f]--面板的抗弯强度设计值(N/mm2);
按以下公式计算面板跨中弯矩:
其中,q--作用在模板上的侧压力,包括:
新浇混凝土侧压力设计值:
q1=1.2×
1×
18×
0.9=19.44kN/m;
倾倒混凝土侧压力设计值:
q2=1.4×
2×
0.9=2.52kN/m;
q=q1+q2=19.440+2.520=21.960kN/m;
计算跨度(内楞间距):
l=250mm;
面板的最大弯距M=0.125×
21.96×
2502=1.72×
105N·
mm;
经计算得到,面板的受弯应力计算值:
σ=1.72×
105/7.35×
104=2.334N/mm2;
面板的抗弯强度设计值:
[f]=13N/mm2;
面板的受弯应力计算值σ=2.334N/mm2小于面板的抗弯强度设计值[f]=13N/mm2,满足要求!
2.挠度验算
q--作用在模板上的侧压力线荷载标准值:
q=21.96N/mm;
l--计算跨度(内楞间距):
E--面板材质的弹性模量:
E=9500N/mm2;
I--面板的截面惯性矩:
I=100×
1.4×
1.4/12=22.87cm4;
面板的最大挠度计算值:
ν=5×
2504/(384×
9500×
2.29×
105)=0.514mm;
面板的最大容许挠度值:
[ν]=l/250=250/250=1mm;
面板的最大挠度计算值ν=0.514mm小于面板的最大容许挠度值[ν]=1mm,满足要求!
四、梁侧模板内外楞的计算
1.内楞计算
内楞(木或钢)直接承受模板传递的荷载,按照均布荷载作用下的三跨连续梁计算。
本工程中,龙骨采用木楞,截面宽度50mm,截面高度100mm,截面惯性矩I和截面抵抗矩W分别为:
W=5×
102×
2/6=166.67cm3;
I=5×
103×
2/12=833.33cm4;
内楞计算简图
(1).内楞强度验算
强度验算计算公式如下:
其中,σ--内楞弯曲应力计算值(N/mm2);
M--内楞的最大弯距(N·
W--内楞的净截面抵抗矩;
[f]--内楞的强度设计值(N/mm2)。
按以下公式计算内楞跨中弯矩:
其中,作用在内楞的荷载,q=(1.2×
0.9+1.4×
0.9)×
1=21.96kN/m;
内楞计算跨度(外楞间距):
l=177mm;
内楞的最大弯距:
M=0.101×
176.672=6.92×
104N·
最大支座力:
R=1.1×
0.177=6.039kN;
经计算得到,内楞的最大受弯应力计算值σ=6.92×
104/1.67×
105=0.415N/mm2;
内楞的抗弯强度设计值:
内楞最大受弯应力计算值σ=0.415N/mm2小于内楞的抗弯强度设计值[f]=13N/mm2,满足要求!
(2).内楞的挠度验算
其中l--计算跨度(外楞间距):
l=500mm;
q--作用在模板上的侧压力线荷载标准值:
q=21.96N/mm;
E--内楞的弹性模量:
9000N/mm2;
I--内楞的截面惯性矩:
I=8.33×
106mm4;
内楞的最大挠度计算值:
ν=0.677×
5004/(100×
9000×
8.33×
106)=0.124mm;
内楞的最大容许挠度值:
[ν]=500/250=2mm;
内楞的最大挠度计算值ν=0.124mm小于内楞的最大容许挠度值[ν]=2mm,满足要求!
2.外楞计算
外楞(木或钢)承受内楞传递的集中力,取内楞的最大支座力6.039kN,按照集中荷载作用下的三跨连续梁计算。
本工程中,外龙骨采用钢楞,截面惯性矩I和截面抵抗矩W分别为:
外钢楞截面抵抗矩W=8.98cm3;
外钢楞截面惯性矩I=21.56cm4;
(1).外楞抗弯强度验算
其中σ--外楞受弯应力计算值(N/mm2)
M--外楞的最大弯距(N·
W--外楞的净截面抵抗矩;
[f]--外楞的强度设计值(N/mm2)。
根据三跨连续梁算法求得最大的弯矩为M=F×
a=1.647kN·
m;
其中,F=1/4×
q×
h=6.588,h为梁高为1.2m,a为次楞间距为250mm;
经计算得到,外楞的受弯应力计算值:
σ=1.65×
106/8.98×
103=183.408N/mm2;
外楞的抗弯强度设计值:
[f]=205N/mm2;
外楞的受弯应力计算值σ=183.408N/mm2小于外楞的抗弯强度设计值[f]=205N/mm2,满足要求!
(2).外楞的挠度验算
其中E-外楞的弹性模量:
206000N/mm2;
F--作用在外楞上的集中力标准值:
F=6.588kN;
l--计算跨度:
l=500mm;
I-外楞的截面惯性矩:
I=215600mm4;
外楞的最大挠度计算值:
ν=1.615×
6588.000×
500.003/(100×
206000.000×
215600.000)=0.299mm;
根据连续梁计算得到外楞的最大挠度为0.299mm
外楞的最大容许挠度值:
[ν]=500/400=1.25mm;
外楞的最大挠度计算值ν=0.299mm小于外楞的最大容许挠度值[ν]=1.25mm,满足要求!
五、穿梁螺栓的计算
验算公式如下:
其中N--穿梁螺栓所受的拉力;
A--穿梁螺栓有效面积(mm2);
f--穿梁螺栓的抗拉强度设计值,取170N/mm2;
查表得:
穿梁螺栓的直径:
14mm;
穿梁螺栓有效直径:
11.55mm;
穿梁螺栓有效面积:
A=105mm2;
穿梁螺栓所受的最大拉力:
N=(1.2×
18+1.4×
2)×
0.5×
0.475=5.795kN。
穿梁螺栓最大容许拉力值:
[N]=170×
105/1000=17.85kN;
穿梁螺栓所受的最大拉力N=5.795kN小于穿梁螺栓最大容许拉力值[N]=17.85kN,满足要求!
六、梁底模板计算
面板为受弯结构,需要验算其抗弯强度和挠度。
计算的原则是按照模板底支撑的间距和模板面的大小,按支撑在底撑上的两跨连续梁计算。
强度验算要考虑模板结构自重荷载、新浇混凝土自重荷载、钢筋自重荷载和振捣混凝土时产生的荷载;
挠度验算只考虑模板结构自重、新浇混凝土自重、钢筋自重荷载。
本算例中,面板的截面惯性矩I和截面抵抗矩W分别为:
W=700×
14×
14/6=2.29×
104mm3;
I=700×
14/12=1.60×
105mm4;
1.抗弯强度验算
按以下公式进行面板抗弯强度验算:
其中,σ--梁底模板的弯曲应力计算值(N/mm2);
M--计算的最大弯矩(kN·
m);
l--计算跨度(梁底支撑间距):
l=250.00mm;
q--作用在梁底模板的均布荷载设计值(kN/m);
新浇混凝土及钢筋荷载设计值:
q1:
1.2×
(24.00+1.50)×
0.70×
1.20×
0.90=23.13kN/m;
模板结构自重荷载:
q2:
1.2×
0.35×
0.90=0.26kN/m;
振捣混凝土时产生的荷载设计值:
q3:
1.4×
2.00×
0.90=1.76kN/m;
q=q1+q2+q3=23.13+0.26+1.76=25.16kN/m;
Mmax=0.125×
25.162×
0.252=0.197kN·
σ=0.197×
106/2.29×
104=8.597N/mm2;
梁底模面板计算应力σ=8.597N/mm2小于梁底模面板的抗压强度设计值[f]=13N/mm2,满足要求!
2.挠度验算
根据《建筑施工计算手册》刚度验算采用标准荷载,同时不考虑振动荷载作用。
最大挠度计算公式如下:
其中,q--作用在模板上的压力线荷载:
q=((24.0+1.50)×
1.200+0.35)×
0.70=21.67KN/m;
E--面板的弹性模量:
E=9500.0N/mm2;
面板的最大允许挠度值:
[ν]=250.00/250=1.000mm;
ν=0.521×
21.665×
2504/(100×
1.60×
105)=0.29mm;
ν=0.29mm小于面板的最大允许挠度值:
[ν]=250/250=1mm,满足要求!
七、梁底支撑的计算
本工程梁底支撑采用钢管。
强度及抗剪验算要考虑模板结构自重荷载、新浇混凝土自重荷载、钢筋自重荷载和振捣混凝土时产生的荷载;
1.荷载的计算:
(1)钢筋混凝土梁自重(kN/m):
q1=(24+1.5)×
0.25=7.65kN/m;
(2)模板的自重线荷载(kN/m):
q2=0.35×
0.25×
(2×
1.2+0.5)/0.5=0.507kN/m;
(3)活荷载为施工荷载标准值与振倒混凝土时产生的荷载(kN/m):
经计算得到,活荷载标准值P1=(2.5+2)×
0.25=1.125kN/m;
2.钢管的支撑力验算
静荷载设计值q=1.2×
7.65+1.2×
0.507=9.789kN/m;
活荷载设计值P=1.4×
1.125=1.575kN/m;
钢管计算简图
钢管按照三跨连续梁计算。
本算例中,钢管的截面惯性矩I和截面抵抗矩W分别为:
W=4.49cm3
I=10.78cm4
钢管强度验算:
最大弯矩考虑为静荷载与活荷载的设计值最不利分配的弯矩和,计算公式如下:
线荷载设计值q=9.789+1.575=11.364kN/m;
最大弯距M=0.1ql2=0.1×
11.364×
0.7×
0.7=0.557kN.m;
最大应力σ=M/W=0.557×
106/4490=124.017N/mm2;
抗弯强度设计值[f]=205N/mm2;
钢管的最大应力计算值124.017N/mm2小于钢管抗弯强度设计值205N/mm2,满足要求!
钢管抗剪验算:
截面抗剪强度必须满足:
其中最大剪力:
V=0.6×
9.789×
0.7=4.111kN;
钢管的截面面积矩查表得A=424.000mm2;
钢管受剪应力计算值τ=2×
4111.380/424.000=19.393N/mm2;
钢管抗剪强度设计值[τ]=120N/mm2;
钢管的受剪应力计算值19.393N/mm2小于钢管抗剪强度设计值120N/mm2,满足要求!
钢管挠度验算:
最大挠度考虑为静荷载与活荷载的计算值最不利分配的挠度和,计算公式如下:
q=7.650+0.507=8.157kN/m;
钢管最大挠度计算值ν=0.677×
8.157×
7004/(100×
206000×
10.78×
104)=0.597mm;
钢管的最大允许挠度[ν]=0.700×
1000/250=2.800mm;
钢管的最大挠度计算值ν=0.597mm小于钢管的最大允许挠度[ν]=2.8mm,满足要求!
3.支撑钢管的强度验算
支撑钢管按照简支梁的计算如下
荷载计算公式如下:
(1)钢筋混凝土梁自重(kN/m2):
q1=(24.000+1.500)×
1.200=30.600kN/m2;
(2)模板的自重(kN/m2):
q2=0.350kN/m2;
(3)活荷载为施工荷载标准值与振倒混凝土时产生的荷载(kN/m2):
q3=(2.500+2.000)=4.500kN/m2;
q=1.2×
(30.600+0.350)+1.4×
4.500=43.440kN/m2;
梁底支撑根数为n,立杆梁跨度方向间距为a,梁宽为b,梁高为h,梁底支撑传递给钢管的集中力为P,梁侧模板传给钢管的集中力为N。
当n=2时:
当n>2时:
计算简图(kN)
变形图(mm)
弯矩图(kN·
m)
经过连续梁的计算得到:
支座反力RA=RB=1.931kN,中间支座最大反力Rmax=12.056;
最大弯矩Mmax=0.29kN.m;
最大挠度计算值Vmax=0.116mm;
最大应力σ=0.29×
106/4490=64.521N/mm2;
支撑抗弯设计强度[f]=205N/mm2;
支撑钢管的最大应力计算值64.521N/mm2小于支撑钢管的抗弯设计强度205N/mm2,满足要求!
八、扣件抗滑移的计算:
按照《建筑施工扣件式钢管脚手架安全技术规范培训讲座》刘群主编,P96页,双扣件承载力设计值取16.00kN,按照扣件抗滑承载力系数0.80,该工程实际的旋转双扣件承载力取值为12.80kN。
纵向或横向水平杆与立杆连接时,扣件的抗滑承载力按照下式计算(规范5.2.5):
R≤Rc
其中Rc--扣件抗滑承载力设计值,取12.80kN;
R--纵向或横向水平杆传给立杆的竖向作用力设计值;
计算中R取最大支座反力,根据前面计算结果得到R=12.056kN;
R<
12.80kN,所以双扣件抗滑承载力的设计计算满足要求!
九、立杆的稳定性计算:
立杆的稳定性计算公式
1.梁两侧立杆稳定性验算:
其中N--立杆的轴心压力设计值,它包括:
水平钢管的最大支座反力:
N1=1.931kN;
脚手架钢管的自重:
N2=1.2×
0.129×
3=0.465kN;
楼板的混凝土模板的自重:
N3=1.2×
(0.80/2+(0.80-0.50)/2)×
0.35=0.162kN;
楼板钢筋混凝土自重荷载:
N4=1.2×
0.200×
(1.50+24.00)=2.356kN;
N=1.931+0.465+0.162+2.356=4.914kN;
φ--轴心受压立杆的稳定系数,由长细比lo/i查表得到;
i--计算立杆的截面回转半径(cm):
i=1.59;
A--立杆净截面面积(cm2):
A=4.24;
W--立杆净截面抵抗矩(cm3):
W=4.49;
σ--钢管立杆轴心受压应力计算值(N/mm2);
[f]--钢管立杆抗压强度设计值:
[f]=205N/mm2;
lo--计算长度(m);
参照《扣件式规范》不考虑高支撑架,按下式计算
lo=k1uh
k1--计算长度附加系数,取值为:
1.155;
u--计算长度系数,参照《扣件式规范》表5.3.3,u=1.7;
上式的计算结果:
立杆计算长度Lo=k1uh=1.155×
1.7×
1.5=2.945m;
Lo/i=2945.25/15.9=185;
由长细比lo/i的结果查表得到轴心受压立杆的稳定系数φ=0.209;
钢管立杆受压应力计算值;
σ=4913.99/(0.209×
424)=55.453N/mm2;
钢管立杆稳定性计算σ=55.453N/mm2小于钢管立杆抗压强度的设计值[f]=205N/mm2,满足要求!
2.梁底受力最大的支撑立杆稳定性验算:
梁底支撑最大支座反力:
N1=12.056kN;
(3-1.2)=0.465kN;
N=12.056+0.465=12.335kN;
σ=12334.837/(0.209×
424)=139.194N/mm2;
钢管立杆稳定性计算σ=139.194N/mm2小于钢管立杆抗压强度的设计值[f]=205N/mm2,满足要求!
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 模板 计算
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 转基因粮食的危害资料摘编Word下载.docx
转基因粮食的危害资料摘编Word下载.docx
