易错题冀教版九年级数学上册期末综合检测试题教师用Word格式文档下载.docx

易错题冀教版九年级数学上册期末综合检测试题教师用Word格式文档下载.docx

《易错题冀教版九年级数学上册期末综合检测试题教师用Word格式文档下载.docx》由会员分享，可在线阅读，更多相关《易错题冀教版九年级数学上册期末综合检测试题教师用Word格式文档下载.docx（24页珍藏版）》请在冰豆网上搜索。

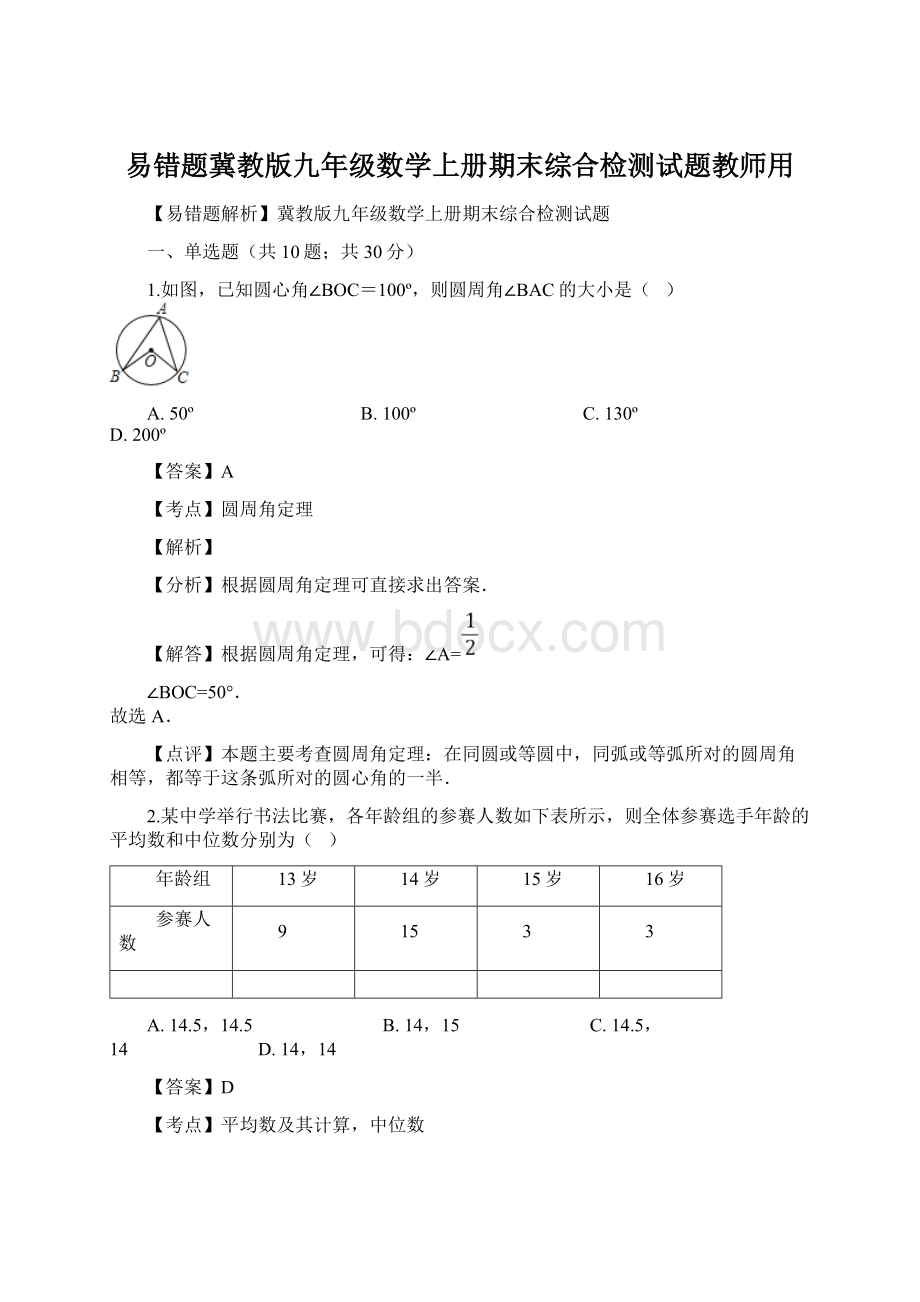
15+15×

3+16×

3）÷

（9+15+3+3）

=（117+210+45+48）÷

30

=420÷

=14

∴全体参赛选手年龄的平均数是14．

∵13岁的有9人，14岁的有15人，15岁的有3人，16岁的有3人，∴把30名参赛选手年龄从小到大排列后，中间两人的年龄分别是14岁、14岁，∴全体参赛选手年龄的中位数是：

（14+14）÷

2=28÷

2=14．

综上，可得全体参赛选手年龄的平均数和中位数分别为14、14．

故答案为：

D．

【分析】一组数据按从小到大的顺序依次排列，处在中间位置的一个数（或最中间两个数据的平均数）.平均数是指在一组数据中所有数据之和再除以数据的个数.

3.新阜宁大桥某一周的日均车流量分别为13，14，11，10，12，12，15（单位：

千辆）,则这组数据的中位数与众数分别为（ 

10，12 

12，10 

12，12 

13，12

【答案】C

【考点】中位数，众数

【解析】【解答】∵从小到大排列为：

10,11,12,12,13,14,15，排在中间的数是12，

∴中位数是12；

∵12出现了2次，出现的次数最多，

∴众数是12.

C.

【分析】将这组数据按从小到大排列，排在最中间的数就是中位数；

这组数据中，出现次数最多的是12，根据众数概念，即可得出答案。

4.（2016•葫芦岛）九年级两名男同学在体育课上各练习10次立定跳远，平均成绩均为2.20米，要判断哪一名同学的成绩比较稳定，通常需要比较这两名同学立定跳远成绩的（ 

方差 

众数 

平均数 

中位数

【考点】常用统计量的选择

由于方差能反映数据的稳定性，需要比较这2名学生立定跳远成绩的方差．

故选：

A．

【分析】根据方差的意义：

是反映一组数据波动大小，稳定程度的量；

方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．故要判断哪一名学生的成绩比较稳定，通常需要比较这2名学生立定跳远成绩的方差．本题考查方差的意义．它是反映一组数据波动大小，方差越大，表明这组数据偏离平均数越大，即波动越大，反之也成立．

5.已知⊙O是△ABC的外接圆，若AB＝AC＝5，BC＝6，则⊙O的半径为（ 

）

4 

3.25 

3.125 

2.25

【考点】三角形的外接圆与外心

取BC中点D，连结AD，OB，

设BO=AO=r，

∵AB=AC=5，BC=6，

∴AD⊥BC，BD=3，

∴AD=4，

在Rt△BOD中，

∴BO2=OD2+BD2，

即r2=32+（4-r）2，

∴r=3.125.

【分析】取BC中点D，连结AD，OB，设BO=AO=r，根据等腰三角形性质可知AD=4，AD⊥BC，在Rt△BOD中，根据勾股定理即可求出半径.

6.如图，港口A在观测站O的正东方向，OA=6m，某船从港口A出发，沿北偏东15°

方向航行一段距离后到达B处，此时从观测站O处测得该船位于北偏东60°

的方向，则该船航行的距离（即AB的长）为（ 

3

m 

4m 

（3

﹣3）m

【考点】解直角三角形的应用﹣方向角问题

作AC⊥OB于点C，如图所示，

由已知可得，

∠COA=30°

，OA=6m，

∵AC⊥OB，

∴∠OCA=∠BCA=90°

，

∴OA=2AC，∠OAC=60°

∴AC=3m，∠CAD=30°

∵∠DAB=15°

∴∠CAB=45°

∴∠CAB=∠B=45°

∴BC=AC，

∴AB=

【分析】根据题意，可以作辅助线AC⊥OB于点C，然后根据题目中的条件，可以求得AC和BC的长度，然后根据勾股定理即可求得AB的长．

7.对于反比例函数y=，下列说法正确的是（ 

图象经过点（1，﹣3） 

图象在第二、四象限

＞0时，y随的增大而增大 

＜0时，y随增大而减小

【考点】反比例函数的图象，反比例函数的性质，反比例函数系数的几何意义

【解析】【解答】A.当=1时，y=3，错误，不符合题意；

B.=3>

0，图象在第一、三象限，错误，不符合题意；

C.=3>

0,在每一个象限内，y随的增大而减小，错误，不符合题意；

D.=3>

0,在每一个象限内，y随的增大而减小，正确，符合题意.

D.

【分析】依据反比例函数的特征，对选项逐个判断，知道得到符合题意的选项.

8.关于的方程（+4）2-2=0是关于的一元二次方程，则的取值范围是（　　）

≠0 

≥4 

=-4 

≠-4 

【考点】一元二次方程的定义

【解析】【解答】由题意得：

+4≠0，

解得：

≠-4，

D．【分析】根据一元二次方程的定义可得+4≠0，再解即可．

9.（2016•湖州）如图1，在等腰三角形ABC中，AB=AC=4，BC=7．如图2，在底边BC上取一点D，连结AD，使得∠DAC=∠ACD．如图3，将△ACD沿着AD所在直线折叠，使得点C落在点E处，连结BE，得到四边形ABED．则BE的长是（ 

2

【答案】B

【考点】等腰三角形的性质，翻折变换（折叠问题），相似三角形的判定与性质

∵AB=AC，

∴∠ABC=∠C，

∵∠DAC=∠ACD，

∴∠DAC=∠ABC，

∵∠C=∠C，

∴△CAD∽△CBA，

∴

=

∴CD=

，BD=BC﹣CD=

∵∠DAM=∠DAC=∠DBA，∠ADM=∠ADB，

∴△ADM∽△BDA，

，即

∴DM=

，MB=BD﹣DM=

∵∠ABM=∠C=∠MED，

∴A、B、E、D四点共圆，

∴∠ADB=∠BEM，∠EBM=∠EAD=∠ABD，

∴△ABD∽△MBE，

∴BE=

故选B．

【分析】只要证明△ABD∽△MBE，得

，只要求出BM、BD即可解决问题．本题考查翻折变换、等腰三角形的判定和性质、相似三角形的判定和性质等知识，解题的关键是充分利用相似三角形的性质解决问题，本题需要三次相似解决问题，题目比较难，属于中考选择题中的压轴题．

10.如图，某小区计划在一块长为32m，宽为20m的矩形空地上修建三条同样宽的道路，剩余的空地上种植草坪，使草坪的面积为570m2．若设道路的宽为，则下面所列方程正确的是（ 

【答案】

【考点】一元二次方程的应用

由题意得，（32−2）（20−）=570【分析】将六块草坪拼为一块可得一个矩形，该矩形面积为六块草坪的面积和570m2。

由图易得新矩形的长为（32−2）m,宽为（20-）m，所以可得方程（32−2）（20−）=570

二、填空题（共10题；

11.某种植物的主干长出a个支干，每个支干又长出同样数目的小分支，则主干、支干和小分支的总数为________.

【答案】1+a+a2

设主干长出a个支干，每个支干又长出a个小分支，

可得该植物的主干，支干和小分支的总数为：

1+a+a2.

1+a+a2

【分析】设主干长出a个支干，每个支干又长出a个小分支，则小分支为

，所以可得总数=主干+支干+小分支。

12.如图，一艘海轮位于灯塔P的北偏东60°

方向，距离灯塔为4海里的点A处，如果海轮沿正南方向航行到灯塔的正东位置，海轮航行的距离AB长________海里．

【答案】2

如图，由题意可知∠NPA=60°

，AP=4海里，∠ABP=90°

∵AB∥NP，

∴∠A=∠NPA=60°

在Rt△ABP中，∵∠ABP=90°

，∠A=60°

，AP=4海里，

∴AB=AP•cos∠A=4×

cos60°

=4×

=2海里．

故答案为2．

【分析】如图，由题意可知∠NPA=60°

．在Rt△ABP中利用余弦函数的定义，由AB=AP•cos∠A即可得出AB的长，

13.已知圆锥的底面半径长为5，侧面展开后得到一个半圆，则该圆锥的母线长为________.

【答案】10

【考点】圆锥的计算

【解析】【解答】设母线长为，根据题意得

2π÷

2=2π×

5，

解得=10．

【分析】根据圆锥侧面展开后得到一个半圆，半圆的周长=圆锥的母线长，依次建立方程求解即可。

14.已知，______

【答案】-4

【考点】比例的性质

设a，

则可以得出：

=2a，y=3a，=5a，

代入中得

原式=．

故答案为-4．

【分析】根据比例的性质求出代数式的值.

15.如图，一块直角三角板ABC的斜边AB与量角器的直径恰好重合，点D对应的刻度是58°

，则∠ACD的度数为________．

【答案】61°

【考点】圆心角、弧、弦的关系，正多边形和圆

【解析】【解答】∵直角三角板ABC的斜边AB与量角器的直径恰好重合，

∴A、B、C、D四点共圆，

又∵点D对应的刻度是58°

∴∠BOD=58°

∴∠BCD=29°

∵∠ACB=90°

∴∠ACD=61°

.

61°

【分析】由已知条件得A、B、C、D四点共圆，根据同弧所对的圆周角等于圆心角的一半得∠BCD=29°

，从而得∠ACD=61°

16.如图，△ABC与△DEF是位似图形，位似比为2：

3，已知AB=4，则DE的长为________．

【答案】6

【考点】位似变换

∵△ABC与△DEF是位似图形，位似比为2：

3，

∴AB：

DE=2：

∴DE=6．

6．

【分析】位似图形的对应边之比等于位似比，因此可求出DE的长。

17.已知关于的方程的个根是1，则m=________．

【考点】解一元一次方程，一元二次方程的根

【解析】【解答】∵关于的方程的个根是1，

∴1﹣3×

1+m=0，解得，m=2，

2．【分析】将=1代入方程，解关于m的方程，求解即可。

18.如图，已知一次函数y=﹣4+5的图象与反比例函数y=（＞0）的图象相交于点A（p，q）．当一次函数y的值随的值增大而增大时，p的取值范围是________．

【答案】

＜p＜4

【考点】反比例函数与一次函数的交点问题

一次函数y=﹣4+5中，令=4，则y=5，故一次函数y=﹣4+5的图象经过点（4，5），

如图所示，过点（4，5）分别作y轴与轴的垂线，分别交反比例函数图象于B点和C点，

把y=5代入y=，得=

；

把=4代入y=，得y=

所以B点坐标为（

，5），C点坐标为（4，

），

因为一次函数y的值随的值增大而增大，

所以点A（p，q）只能在B点与C点之间的曲线上，

所以p的取值范围是

＜p＜4．

【分析】先根据一次函数的解析式，得到一次函数y=﹣4+5的图象经过点（4，5），过点（4，5）分别作y轴与轴的垂线，分别交反比例函数图象于B点和C点，根据点A（p，q）只能在B点与C点之间，即可求得p的取值范围是

19.如图，在△ABC中，∠C=90°

，BC=16cm，AC=12cm，点P从点B出发，沿BC以2cm/s的速度向点C移动，点Q从点C出发，以1cm/s的速度向点A移动，若点P、Q分别从点B、C同时出发，设运动时间为ts，当t=________时，△CPQ与△CBA相似．

【答案】4.8或

【考点】勾股定理，相似三角形的判定

CP和CB是对应边时，△CPQ∽△CBA，

所以，

即

解得t=4.8；

CP和CA是对应边时，△CPQ∽△CAB，

解得t=

综上所述，当t=4.8或

时，△CPQ与△CBA相似．

故答案为4.8或

【分析】△CPQ与△CBA相似可分为两类：

△CPQ∽△CBA或△CPQ∽△CAB，用t的代数式表示边，对应边成比例列出方程即可.

20.如图，在四边形ABCD中，AD∥BC，∠BCD=90°

，∠ABC=45°

，AD=CD，CE平分∠ACB交AB于点E，在BC上截取BF=AE，连接AF交CE于点G，连接DG交AC于点H，过点A作AN⊥BC，垂足为N，AN交CE于点M．则下列结论：

①CM=AF；

②CE⊥AF；

③△ABF∽△DAH；

④GD平分∠AGC，

其中正确的序号是________．

【答案】①②③④

【考点】全等三角形的判定与性质，相似三角形的判定与性质

⑴结论①正确．理由如下：

∵∠1=∠2，∠1+∠CMN=90°

，∠2+∠6=90°

∴∠6=∠CMN，又∵∠5=∠CMN，

∴∠5=∠6，

∴AM=AE=BF．

易知ADCN为正方形，△ABC为等腰直角三角形，∴AB=AC．

在△ACM与△ABF中，

∴△ACM≌△ABF（SAS），

∴CM=AF；

⑵结论②正确．理由如下：

∵△ACM≌△ABF， 

∴∠2=∠4，

∵∠2+∠6=90°

∴∠4+∠6=90°

∴CE⊥AF；

⑶结论③正确．理由如下：

证法一：

∵CE⊥AF，

∴∠ADC+∠AGC=180°

∴A、D、C、G四点共圆，

∴∠7=∠2，

∵∠2=∠4，

∴∠7=∠4，

又∵∠DAH=∠B=45°

∴△ABF∽△DAH；

证法二：

∵CE⊥AF，∠1=∠2，

∴△ACF为等腰三角形，AC=CF，点G为AF中点．

在Rt△ANF中，点G为斜边AF中点，

∴NG=AG，

∴∠MNG=∠3，

∴∠DAG=∠CNG．

在△ADG与△NCG中，

∴△ADG≌△NCG（SAS），

∴∠7=∠1，

又∵∠1=∠2=∠4，

⑷结论④正确．理由如下：

∵A、D、C、G四点共圆，

∴∠DGC=∠DAC=45°

，∠DGA=∠DCA=45°

∴∠DGC=∠DGA，即GD平分∠AGC．

∵AM=AE，CE⊥AF，

∴∠3=∠4，又∠2=∠4，∴∠3=∠2

则∠CGN=180°

﹣∠1﹣90°

﹣∠MNG=180°

﹣∠3=90°

﹣∠1﹣∠2=45°

∵△ADG≌△NCG，

∴∠DGA=∠CGN=45°

=

∠AGC，

∴GD平分∠AGC．

综上所述，正确的结论是：

①②③④，共4个．

①②③④

【分析】结论①正确，证明△ACM≌△ABF即可；

结论②正确，由△ACM≌△ABF得出∠2=∠4，进而得∠4+∠6=90°

，即CE⊥AF，结论③正确，证法一：

利用四点共圆；

利用三角形全等；

结论④正确，证法一：

利用四点共圆，证法二：

利用三角形全等。

三、解答题（共7题；

共60分）

21.如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.

（1）在图上标出位似中心D的位置,并写出该位似中心D的坐标是 

（2）求△ABC与△A′B′C′的面积比．

【答案】解：

（1）如图：

D（7，0）；

（2）∵△ABC∽△A′B′C′

∴

【考点】相似三角形的性质，作图﹣位似变换

【解析】【分析】考查位似.

22.我市一家电子计算器专卖店每只进价13元，售价20元，为了扩大销售，该店现规定，凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低0.10元，例如，某人买20只计算器，于是每只降价0.10×

（20－10）=1（元），因此，所买的全部20只计算器都按照每只19元计算，但是最低价为每只16元。

问一次卖多少只获得的利润为120元？

设一次卖只，所获得的利润为120元，根据题意得：

[20-13-0.1（-10）]=120

解之得：

=20或=60（舍去）。

（因为最多降价到16元，所以60舍去。

答：

一次卖20只时利润可达到120元。

【解析】【分析】设一次卖只，所获得的利润为120元，根据我市一家电子计算器专卖店每只进价13元，售价20元，为了扩大销售，该店现规定，凡是一次买10只以上的，每多买1只，所买的全部计算器每只就降低0.10元，可列方程求解。

23.如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC＝∠D＝60°

（1）求∠ABC的度数；

（2）求证：

AE是⊙O的切线；

（3）当BC＝4时，求劣弧AC的长．

（1）解：

∵∠ABC与∠D都是弧AC所对的圆周角，∴∠ABC＝∠D＝60°

（2）证明：

∵AB是⊙O的直径，

∴∠ACB＝90°

∴∠BAC＝30°

∴∠BAE＝∠BAC＋∠EAC＝30°

＋60°

＝90°

即BA⊥AE，∴AE是⊙O的切线．

（3）解：

如图，连接OC.

∵OB＝OC，∠ABC＝60°

∴△OBC是等边三角形，

∴OB＝BC＝4，∠BOC＝60°

∴∠AOC＝120°

∴弧AC的长度为＝

＝

π.

【考点】切线的判定，弧长的计算

【解析】【分析】考查切线的判定。

24.如图所示，某教学活动小组选定测量小山上方某信号塔PQ的高度，他们在A处测得信号塔顶端P的仰角为45°

，信号塔低端Q的仰角为31°

，沿水平地面向前走100米到处，测得信号塔顶端P的仰角为68°

．求信号塔PQ的高度．（结果精确到0.1米．参考数据：

sin68°

≈0.93，cos68°

≈0.37，tan68°

≈2.48，tan31°

≈0.60，sin31°

≈0.52，cos31°

≈0.86）

延长PQ交直线AB于点M，

则∠PMA＝90°

，设PM的长为米，根据题意，

得∠PAM＝45°

，∠PBM＝68°

，∠QAM＝31°

AB＝100，∴在Rt△PAM中，AM＝PM＝．

BM＝AM－AB＝－100， 

在Rt△PBM中，∵tan∠PBM＝

即tan68°

＝．解得≈167.57．∴AM＝PM≈167.57．

在Rt△QAM中，∵tan∠QAM＝

∴QM＝AM·

tan∠QAM＝167.57×

tan31°

≈100.54． 

∴PQ＝PM－QM＝167.57－100.54≈67.0（米）．

因此，信号塔PQ的高度约为67.0米

【考点】解直角三角形的应用﹣仰角俯角问题

【解析】【分析】延长PQ交直线AB于点M，则∠PMA＝90°

，设PM的长为米，根据题意，得∠PAM＝45°

，AB＝100，根据等腰直角三角形的性质得出AM＝PM＝，BM＝AM－AB＝－100， 

根据正切函数的定义，由tan∠PBM＝

，即可建立方程，从而算出AM＝PM≈167.57, 

根据正切函数的定义，由QM＝AM·

tan∠QAM算出QM的长，根据线段的和差，由PQ＝PM－QM算出答案。

25.如图，已知A（n，﹣2），B（1，4）是一次函数y=+b的图象和反比例函数y=的图象的两个交点，直线AB与y轴交于点C．

（1）求反比例函数和一次函数的关系式；

（2）求△AOC的面积；

（3）求不等式+b﹣＜0的解集．（直接写出答案）

（1）∵B（1，4）在反比例函数y=上，

∴m=4，

又∵A（n，﹣2）在反比例函数y=的图象上，

∴n=﹣2，

又∵A（﹣2，﹣2），B（1，4）是一次函数y=+b的上的点，联立方程组解得，

=2，b=2，

∴y=，y=2