北京高考数学试卷理科.docx

北京高考数学试卷理科.docx

《北京高考数学试卷理科.docx》由会员分享，可在线阅读，更多相关《北京高考数学试卷理科.docx（6页珍藏版）》请在冰豆网上搜索。

2018年普通高等学校招生全国统一考试

数学（理）（北京卷）

一、选择题共8小题，每小题5分，共40分，在每小题列出的四个选项中，选出符合题目要求的一项。

（1）已知集合A＝{x|x|<2}，，B＝{-2，0，1，2}，则A∩B＝（ ）

A．{0，1} B．{-1，0，1}

C．{-2，0，1，2} D．{-1，0，1，2}

（2）在复平面内，复数的共轭复数对应的点位于（）

A．第一象限 B．第二象限

C．第三象限 D．第四象限

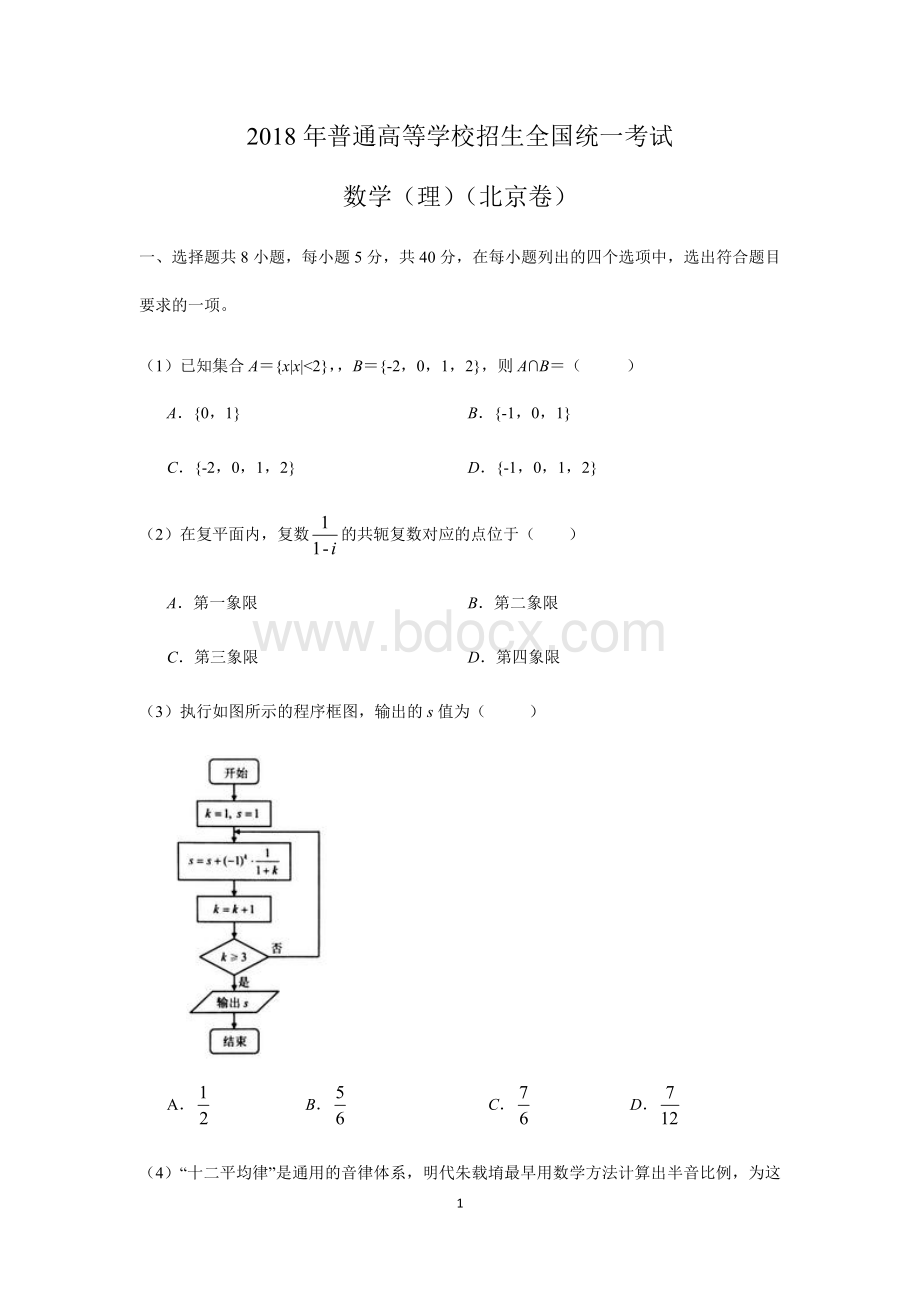
（3）执行如图所示的程序框图，输出的s值为（ ）

A． B． C． D．

（4）“十二平均律”是通用的音律体系，明代朱载堉最早用数学方法计算出半音比例，为这个理论的发展做出了重要贡献，十二平均律将一个纯八度音程分成十二份，依次得到十三个单音，从第二个单音起，每一个单音的频率与它的前一个单音的频率的比都等与。

若第一个单音的频率为f，则第八个单音的频率为（ ）

A．B．C．D．

（5）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（ ）

A．1B．2C．3D．4

（6）设a，b均为单位向量，则“|a－3b|=|3a+b|”是“a⊥b”的（ ）

A．充分而不必要条件　　　　　 B．必要而不充分条件

C．充分必要条件 D．既不充分也不必要条件

（7）在平面直角坐标系中，记d为点p（cosθ，sinθ）到直线x-my-2=0的距离。

当θ，m变化时，d的最大值为（）

A．1B．2C．3D．4

（8）设集合A＝{（x，y）|x－y≥1，ax+y>4，x-ay≤2}，则（）

A．对任意实数a，（2，1）∈AB．对任意实数a，（2，1）A

C．当且仅当a<0时，（2，1）AD．当且仅当a≤时，（2，1）A

第二部分（非选择题共110分）

二、填空题共6小题，每小题5分，共30分。

（9）设{an}是等差数列，且a1＝3，a2＋＝36，则{an}的通项公式为______________.

（10）在极坐标系中，直线ρcosθ＋ρsinθ＝a（a>0）与圆ρ＝2cosθ相切，则a＝________.

（11）设函数f（x）=cos（ωx-），若f（x）≤f（）对任意的实数x都成立，则ω的最小值为______.

（12）若x，y满足x+1≤y≤2x，则2y-x的最小值是__________.

（13）能说明“若f（x）>f（0）对任意的x∈（0，2]都成立，则f（x）在[0，2]是增函数”为假命题的一个函数是______________.

（14）已知椭圆椭圆M：

＋＝1（a>b>0），双曲线N：

，若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点，则椭圆M的离心率为________，双曲线的离心率为________.

三、解答题共6小题，共80分，解答应写出文字说明，验算步骤或证明过程。

（15）（本小题13分）

在△ABC中，a=7，b=8，cosB=.

（I）求A；

（II）求AC边上的高。

（16）（本小题14分）

如图，在三棱柱ABC－A1B1C1中，CC1⊥平面ABC，D,E,F,G分别为AA1,AC,A1C1，BB1的中点，AB=BC=，AC=AA1=2.

（1）求证：

AC⊥平面BEF；

（2）求二面角B-CD-C1的余弦值；

（3）证明：

直线FG与平面BCD相交。

（17）（本小题12分）

电影公司随机收集了电影的有关数据，经分类整理得到下表：

电影类型

第一类

第二类

第三类

第四类

第五类

第六类

电影部数

140

50

300

200

800

510

好评率

0.4

0.2

0.15

0.25

0.2

0.1

好评率是指：

一类电影中获得好评的部数与该类电影的部数的比值。

假设所有电影是否获得好评相互独立。

（1）从电影公司收集的电影中随机选取1部，求这部电影是获得好评的第四类电影的概率；

（2）从第四类电影和第五类电影中各随机选取1部，估计恰好有1部获得好评的概率；

（3）假设每类电影得到人们喜欢的概率与表格中该类电影的好评率相等，用“”表示第k类电影得到人们喜欢，“”表示第k类电影没有得到人们喜欢（k=1,2,3,4,5,6）,写出方差的大小关系。

（18）（本小题13分）

设函数f（x）=[]

（1）若曲线y=f（x）在点（1，f

（1））处的切线与x轴平行，求a;

（2）若f（x）在x=2处取得极小值，求a的取值范围。

（19）（本小题14分）

已知抛物线C：

经过点（1，2），过点Q（0，1）的直线l与抛物线C有两个不同的交点A，B，且直线PA交y轴于M，直线PB交y轴于N。

（1）求直线l的斜率的取值范围；

（2）设O为原点，，，求证：

为定值。

（20）（本小题14分）

设n为正整数，集合A={α|α=}，对于集合A中的任意元素α=（）和β=（）记

M（α，β）=

（1）当n=3时，若α=（1，1，0），β=（0，1，1），求M（α，α）和M（β，β）的值；

（2）当n=4时，设B是A的子集，且满足：

对于B中的任意元素α，β，当α，β相同时，M（α，β）是奇数；当α，β不同时，M（α，β）是偶数，求集合B中元素个数的最大值；

（3）给定不小于2的n，设B是A的子集，且满足：

对于B中的任意两个不同的元素α，β，M（α，β）=0，写出一个集合B，使其元素个数最多，并说明理由。

6