长正方体公式及概念Word格式.docx

长正方体公式及概念Word格式.docx

《长正方体公式及概念Word格式.docx》由会员分享，可在线阅读，更多相关《长正方体公式及概念Word格式.docx（12页珍藏版）》请在冰豆网上搜索。

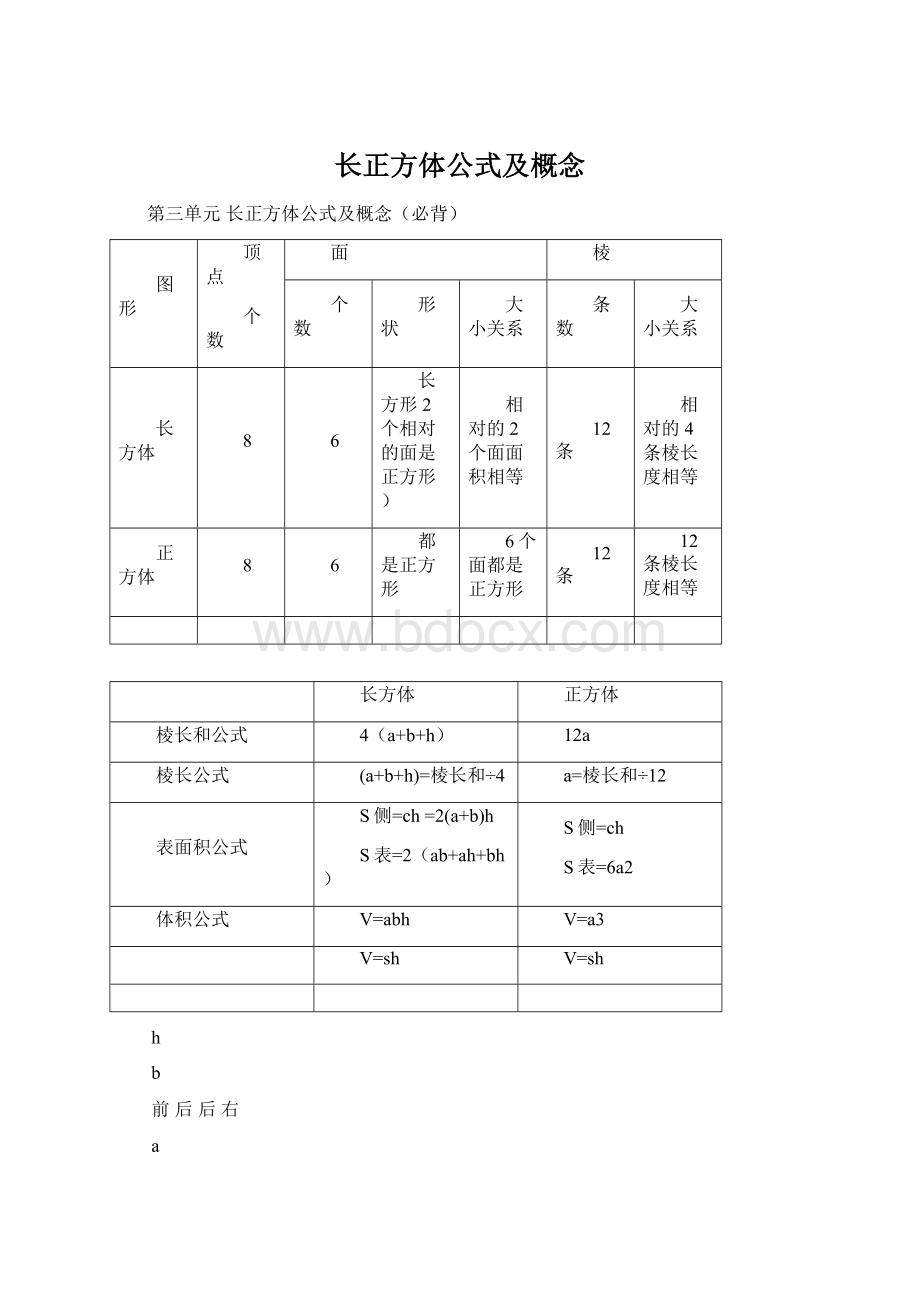
表面积公式

S侧=ch=2（a+b）h

S表=2（ab+ah+bh）

S侧=ch

S表=6a2

体积公式

V=abh

V=a3

V=sh

h

b

前后后右

a

前（后）面=ah

左（右）面=bh长方体侧面积=2（前面+右面）

上（下）面=ab=2（ah+bh）

长方体侧面积=底面周长×

高

=2（a+b）h

面积：

物体表面或平面图形的大小

体积：

物体所占空间的大小叫做物体的体积。

1m3=1000dm31L=1000mL1L=1dm3

1dm3=1000cm31mL=1cm3

第三章

（一）长方体和正方体的认识

★

一、填空题

1、长方体有（）个面，（）条棱，（）个顶点。

2、长方体的6个面一般是（）形，也可能有相对的两个面是（）形。

二、判断题

1、有6个面，8个顶点，12条棱的物体都是长方体。

（）

2、正方体是一种特殊的长方体。

（）

3、长方体每相邻两个面完全相同。

4、长方体的每个面都是长方形。

三、其它题型

1、填表。

相同点

不同点

面的形状

面的大小

棱的长度

长

方

体

个

条

由6个（）形围成的立体图形，特殊情况有两个相对的面是（）形。

相对的面

相对的棱

正

形

都是完全相同的（）形。

面积都（）

棱都（）

通过上表，可以知道长方体和正方体的关系是：

★★

一、填空题

1、一个长方体的长是12厘米，宽8厘米，高6厘米，它的棱长和是（）厘米。

2、这个正方体的棱长的和是（）分米。

3、用上图（右）3根铁丝的长度作为长、宽、高，做一个长方体框架，共需要铁丝（）厘米。

4、有一个正方体，棱长是7厘米，它的棱长之和是（）厘米。

二、选择题

1、用一根60厘米的铁丝可以折成棱长是（）厘米的正方体。

A．5B．12C．10

2、一个长方体的长是9厘米，宽是7厘米，高是4厘米，这个长方体的棱长总和是（）

A．40厘米B．80厘米C．63厘米

3、一个长方体的棱长总和是72厘米，这个长方体的长、宽、高的和是（）厘米。

A．24B．18C．36

2、计算下面长方体棱长和。

（1）

（2）

3、解决问题。

（1）一个正方体的棱长是6厘米，它的棱长之和是多少？

（2）用一根24厘米长的铁丝焊成一个长方体框架，这个长方体框架的棱长是多少厘米？

（3）一个长方体有两个相对的面是正方形，正方形的边长是5cm，这个长方体的棱长之和是100厘米，它的高是多少厘米？

（4）一个正方体，相交于同一个顶点的三条棱长度的和是12分米。

这个正方体的棱长的总和是多少？

★★★

用一根绳子捆扎一种礼盒，如果结头处的绳子长30厘米，求这根绳子的长度。

第三章

（二）长方体和正方体的表面积

★一、填空题

1、长方体或正方体（），叫做它的表面积。

2、看图填空：

①前面的面积是（）。

②左、右两个面，面积的和是（）。

③上、下两个面，面积的和是（）。

④表面积是（）。

3、一个正方体的棱长是5厘米，它的面积是（）。

4、有一个长方体的长是12厘米，宽6厘米，高8厘米，把它放在桌面上，它占用桌面的面积最大是（）平方厘米，最小是（）平方厘米。

1、要做一个无盖的长方体玻璃鱼缸，长60厘米，宽50厘米，高40厘米，至少要用（）平方厘米的玻璃。

A．14800B．11800C．12800

三、其它题型

1、用纸板做一个长15米，宽8米，高2米的长方体纸箱，至少要用纸板多少平方米？

1、一个正方体的表面积是54平方米，它的每个面的面积是（）平方米。

2、一个正方体的表面积是96平方分米，它的每个面的面积是（）平方分米，它的棱长是（）分米。

3、一个长方体的底面积是48平方厘米，宽和高都是4厘米，这个长方体的表面积是（）平方厘米。

4、两个完全一样的正方体拼成一个长方体后，表面积比原来小（）个面的面积。

5、一个长方体的长是5厘米，宽是4厘米，高是2厘米，它的最大面的面积是（）。

二、选择题

1、把一块长方体的木块，平均锯成两块后，木块的表面积和原来比较，（）

A．减少了B．增加了C．没有变化

2、大正方体的表面积是小正方体的4倍，那么大正方体的棱长是小正方体棱长的（）倍。

A．2B．4C．6D．8

3、将一个大长方体从一角切去一个小正方体,切后图形表面积和原长方体表面积相比，（）

A．比原来的表面积大B．一样大C．比原来的表面积小

1、右图是一个长方体的长、宽、高，

请你把它画完整（不要求用虚线

画看不见的部分）。

2、用铁皮焊接一个长方体无盖水槽，长

米，宽0.8米，深2米，需要铁皮多少平方米？

（焊接损耗不计）

3、有一个长方体的茶叶桶，长和宽都是8cm，高是12cm。

在桶的四周贴上商标纸，这张商标纸的面积是多少平方厘米？

（接头处忽略不计）

4、先列式计算，再把表格填写完整。

5、学校粉刷教室的房顶和四壁预算表

教室长（米）

10

教室宽（米）

教室高（米）

门窗面积（平方米）

15.5

每平方米用涂料约（千克）

3

需购买涂料约（千克）

6、

把三个棱长是4厘米的小正方体拼成一个大长方体，这个长方体的表面积是多少平方厘米？

7、一个长方体的底面周长是24厘米，高6厘米，求这个长方体周围四个面的面积总和是多少平方厘米？

1、正方体的棱长扩大2倍，它的表面积就扩大（）倍。

1、长方体的长、宽、高都扩大2倍，表面积扩大6倍。

（）

三、

其它题型

1、下面的图形中，哪一个可以折成正方体，在下面的（）里画“√”。

2、把6个棱长是1厘米的小正方体拼成一个大长方体，拼成长方体表面积最小是多少平方厘米？

3、有一块铁皮（如图），从四个顶点分别剪去一个边长2厘米的正方形，所剩的部分正好焊接成一个无盖的正方体铁皮盒。

原铁皮的面积是多少平方厘米？

4、将12盒磁带按“规则方式”打包，所谓“规则方式”是指每相邻两盒必须是以全等的面积对接，最后得到的包装形状是一个长方体。

已知磁带盒的长为11厘米，宽为7厘米，高为2厘米。

按“规则方式”打包后得到的长方体的表面积最小值是多少平方厘米？

5、有一个正方体，第一次切成两个完全一样的长方体，然后又切成了四个完全一样的长方体，最后再切成八个完全一样的正方体。

这时小正方体的表面积之和比原来大正方体增加了15平方厘米。

大正方体的表面积是多少？

第三章（三）长方体和正方体的体积

1、物体所占（）的大小叫做物体的体积。

2、在日常生活中，常用的体积单位有（）、（）和（）。

3、计量液体常用的体积单位是（）和（）。

4、相邻两个体积单位间的进率是（）。

5、棱长是（）的正方体的体积是1立方米。

6、在工程上，“

”的土、沙石等均简称（）。

7、一个正方体的棱长是

。

这个正方体的棱长和是（）；

表面积是（）；

体积是（）。

8、一个长方体长

，宽

，高

，它的体积是（）。

9、右图中每个小正方体的体积都是

，拼成的大长方体的长是（）cm，宽是（）cm，高是（）cm，体积是（）

1、下图中表示体积的是：

2、一个长方体的长是a，宽是b，高是h，它的体积是（）。

A．2（ab+ah+bh）B．2（a+b+h）C．a×

b×

c

3、一个油桶能盛200升汽油，我们就说这个油桶的（）是200升。

A．体积B．质量C．容积

三、判断题

1、容积和体积的计算方法相同，所以物体的体积等于容积。

2、相邻的两个体积单位间的进率是1000，所以体积单位比面积单位大。

3、正方体的体积比表面积大。

4、两个表面积相等的正方体体积一定相等。

5、5立方米比3平方米大。

6、把一个正方体切成两块后，表面积和体积都不变。

7、

表示3个a相加。

8、棱长为6厘米的正方体的表面积和体积相等。

四、其它题型

1、填表

长（cm）

宽（cm）

高（cm）

体积（

）

5

1.2

2

3.6

54

棱长（cm）

2、计算下面长方体和正方体的体积和表面积。

（单位：

cm）

3、在括号里填上合适的单位名称。

一瓶墨水是32（）；

拖拉机油箱的容积是12（）；

喷雾器的体积是15（）

药液箱的容积是14（）；

电冰箱的体积大约是210（）；

一张写字台大约占地2（）

★★一、填空题

1、一个正方体的棱长之和是72厘米，它的表面积是（），体积是（）。

2、长方体的长、宽、高各缩小2倍，它的体积缩小（）倍。

3、四个同学分别用8个1立方厘米的立方体测量了4个盒子的容积，第（）个盒子容积最大，是（）立方厘米。

1、底面积是36平方分米的正方体,体积是（）立方米。

A．216B．2160000C．0.216

2、体积为8立方厘米的正方体积木，放在桌子上所占桌面的面积是（）

A．8平方厘米B．4平方厘米C．4立方厘米D．16平方厘米

1、正方体的边长扩大5倍，它的体积就扩大5倍。

2、长方体的长扩大2倍，宽缩小2倍，高不变，这个长方体的体积不变。

1、要制作60个棱长是0.4dm的正方体木块，要损耗木材多少立方分米？

2、学校要修建一个游泳池，游泳池长25米，宽15米，深1.6米。

一台挖土机如果每小时能挖土50方，几小时能挖完？

3、一根长3m的长方体枕木，横截面是边长0.3m的正方形。

每立方米枕木质量是3.2吨，这根枕木的质量是多少吨？

4、把一块棱长为40厘米的正方体钢块，熔成一根长80厘米，厚40厘米的钢条。

这根钢条宽多少厘米？

1、一个长方体木块，长12.5dm，如果沿着与高平行的方向把它切成两个长方体，这两个长方体的表面积的和比原长方体表面积增加

原长方体的体积是多少？

2、一个长40厘米的长方体，它的横截面是正方形，如果长增加5厘米，表面积就增加80平方厘米，求原长方体的表面积和体积。

3、下面的长方体都是用棱长1厘米的小正方体摆成的。

算出它们的体积。

★★★★

1、一个底面是正方形的长方体的纸箱，如果把它的侧面展开，可以得到一个长120cm，宽是80cm的长方形。

这个纸箱的体积可能是多少？

（两个答案你都能求出来吗？

2、有一个长方体容器，从里面量长6分米，宽5分米，高8分米，里面注有水，水深4分米。

如果把一块边长3分米的正方体铁块浸入水中，水面上升多少分米？

3、一个边长为4厘米的正方体，分别在它的前后、左右、上下各面的

中心位置打一个直穿木块的洞，洞口为边长1厘米的正方形（如图）。

求挖洞后木块的体积及表面积。

第一关:

运用公式填一填

1.一个长方体的长是5厘米,宽是4厘米,高是3厘米,它的表面积是（）平方厘米。

2.一个正方体的棱长之和是24厘米,它的表面积是（）平方厘米。

3.一个长方体的长是4.2分米,宽是3分米,高是2分米,一个正方体的表面积和这个长方体的表面积相等,这个正方体一个面的面积是（）平方分米。

第二关:

细心读题辩一辩

1.如果一个长方体和一个正方体的所有棱长之和相等,那么它们的表面积相（）

2.一个长方体的长、宽、高都扩大2倍,它的表面积就扩大8倍。

3.正方体的棱长扩大3倍,表面积就扩大9倍。

第三关:

联系实际用一用

1.（如图）根据图中标注的茶叶筒的有关尺寸,请你算出商标的面积.

2．（如图）手提袋的长是25厘米,宽是10厘米,高是45厘米.做一个这样的手提袋大约需要多少平方厘米的硬纸板?

第四关：

仔细观察算一算

请你算出下面图形的表面积.（单位:

厘米）

第五关：

细心读题比一比

1.把一个长方体切成两个大小完全相同的正方体,这时表面积增加了40平方分米.原来长方体的表面积是多少平方分米?

2.把一个长方体切成三个完全相同的正方体,这三个正方体的表面积之和比原来长体的表面积大8平方厘米.原来长方体的表面积是多少平方厘米?

3.把一个长方体接上一个正方体后,表面积比原来增加80平方厘米.接上的正方体的表面积是多少平方厘米?

4.一个正方体和一个长方体拼在一起成为一个新的长方体,新的长方体的表面积比原来长方体的表面积增加90平方厘米.原来正方体的表面积是多少平方厘米?

第六关：

放飞思维想一想

1.一个长方体,长10分米,宽8分米,高2分米.现要求只锯一次,锯成两个长方体,表面积可能增加多少平方分米?

2.用12个棱长是1厘米的小正方体拼成一个新的长方体,拼成的长方体的表面积可能是多少平方厘米?

3.从一块长3分米、宽2分米、高1分米的长方体木料上截取一个尽可能大的小正方体,剩下木料的面积可能是多少?