初中数学几何证明题模型.ppt

初中数学几何证明题模型.ppt

《初中数学几何证明题模型.ppt》由会员分享，可在线阅读，更多相关《初中数学几何证明题模型.ppt（34页珍藏版）》请在冰豆网上搜索。

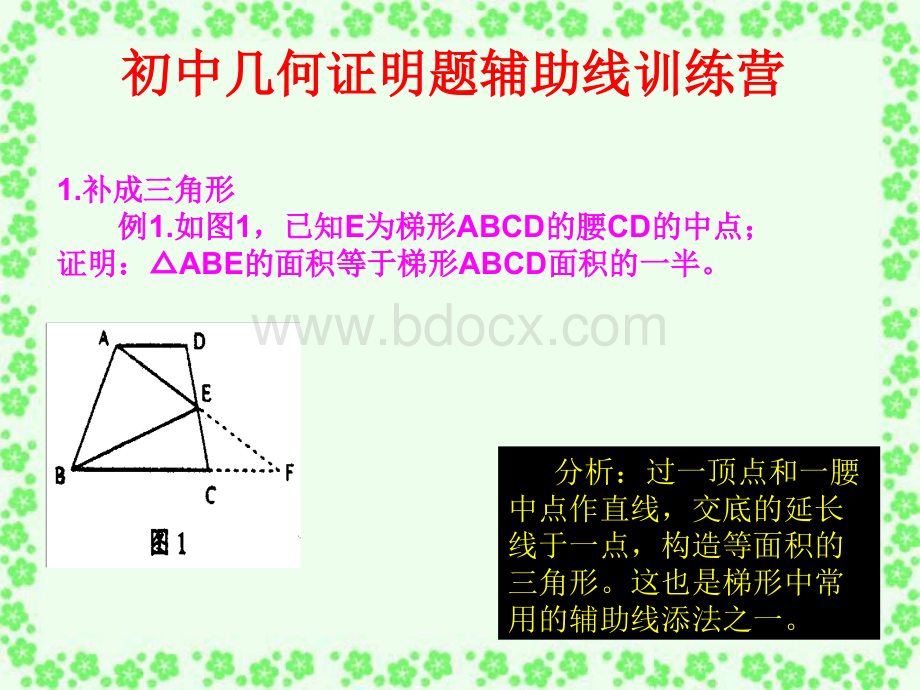
1.补成三角形补成三角形例例1.如图如图1，已知，已知E为梯形为梯形ABCD的腰的腰CD的中点；的中点；证明：

证明：

ABE的面积等于梯形的面积等于梯形ABCD面积的一半。

面积的一半。

初中几何证明题辅助线训练营初中几何证明题辅助线训练营分析：

过一顶点和一腰中点作直线，交底的延长线于一点，构造等面积的三角形。

这也是梯形中常用的辅助线添法之一。

分析：

因为角是分析：

因为角是轴对称图形，角平分轴对称图形，角平分线是对称轴，故根据线是对称轴，故根据对称性作出辅助线，对称性作出辅助线，不难发现不难发现CFCF2CE2CE，再证再证BDBDCFCF即可。

即可。

2.补成等腰三角形补成等腰三角形例例2如图如图2.已知已知A90，ABAC，12，CEBD，求证：

，求证：

BD2CE3.补成直角三角形补成直角三角形例例3.如图如图3，在梯形，在梯形ABCD中，中，ADBC，BC90，F、G分别是分别是AD、BC的中点，若的中点，若BC18，AD8，求，求FG的长。

的长。

分析：

从B、C互余，考虑将它们变为直角三角形的角，故延长BA、CD，要求FG，需求PF、PG。

图图334.补成等边三角形补成等边三角形例例4.图图4，ABC是等边三角形，延长是等边三角形，延长BC至至D，延长，延长BA至至E，使，使AEBD，连结，连结CE、ED。

证明：

。

证明：

ECED分析：

要证明ECED，通常要证ECDEDC，但难以实现。

这样可采用补形法即延长BD到F，使BFBE，连结EF。

5.补成平行四边形补成平行四边形例例5.如图如图5，四边形，四边形ABCD中，中，E、F、G、H分别是分别是AB、CD、AC、BD的中点，并且的中点，并且E、F、G、H不在同一条直上，不在同一条直上，求证：

求证：

EF和和GH互相平分。

互相平分。

分析：

因为平行四边形的对角线互相平分，故要证结论，需考虑四边形GEHF是平行四边形。

6.补成矩形补成矩形例例6.如图如图6，四边形，四边形ABCD中，中，A60，BD90，AB200m，CD100m，求，求AD、BC的长。

的长。

分析：

矩形具有许多特殊的性分析：

矩形具有许多特殊的性质，巧妙地构造矩形，可使问质，巧妙地构造矩形，可使问题转化为解直角三角形，于是题转化为解直角三角形，于是一些四边形中较难的计算题不一些四边形中较难的计算题不难获解。

难获解。

图图667.补成菱形补成菱形例例7.如图如图7，凸五边形，凸五边形ABCDE中，中，A=B120，EAABBC2，CDDE4，求其面积，求其面积分析：

延长EA，CB交于P，根据题意易证四边形PCDE为菱形。

图图778.补成正方形例8.如图8，在ABC中，ADBC于D，BAC45，BD3，DC2。

求ABC的面积。

图图88分析：

本题要想从已知条件直接求出此三角形的面积确实有些困难，如果从题设BAC45，ADBC出发，可以捕捉到利用轴对称性质构造一个正方形的信息，那么问题立即可以获解。

9.补成梯形补成梯形例例9如图如图9，已知，已知：

G是是ABC中中BC边上的中线的中点，边上的中线的中点，L是是ABC外的一条直线，自外的一条直线，自A、B、C、G向向L作垂线，垂足作垂线，垂足分别为分别为A1、B1、C1、G1。

求证：

。

求证：

GG11/4（2AA1BB1CC1）。

图图99分析：

本题从已知条件可知，中点多、垂线多特点，联想到构造直角梯形来加以解决比较恰当，故过D作DD1L于D1，则DD1既是梯形BB1C1C的中位线，又是梯形DD1A1A的一条底边，因而，可想到运用梯形中位线定理突破，使要证的结论明显地显示出来，从而使问题快速获证。

11、在、在ABCABC中，中，AC=BCAC=BC，DD是是ACAC上一点，且上一点，且AEAE垂直垂直BDBD的延长的延长线于线于EE，又，又AE=BDAE=BD，求证：

，求证：

BEBE平分平分ABCABC。

课后作业：

课后作业：

22、如图，已知：

在、如图，已知：

在ABCABC内，内，BAC=60BAC=60，ACB=40ACB=40，PP、QQ分别在分别在BCBC、CACA上，并且上，并且APAP、BQBQ分别是分别是BACBAC、ABCABC的角平的角平分线，求证：

分线，求证：

BQ+AQ=AB+BPBQ+AQ=AB+BP33、已知：

、已知：

BAC=90BAC=90，AB=ACAB=AC，AD=DCAD=DC，AEBDAEBD，求证：

，求证：

ADB=CDEADB=CDE44、设正三角形、设正三角形ABCABC的边长为的边长为22，MM是是ABAB边上的中点，边上的中点，PP是是BCBC边边上的任意一点，上的任意一点，PA+PMPA+PM的最大值和最小值分别记为的最大值和最小值分别记为SS和，求：

和，求：

SStt的值。

的值。

5.5.ABCABC中，分别以中，分别以AB,AC,BCAB,AC,BC为边在同侧作等边三角形为边在同侧作等边三角形ABD,BCF,ACEABD,BCF,ACE探究下探究下列问题列问题（11）当当ABCABC满足满足_条件时，四边形条件时，四边形DAEFDAEF是矩形是矩形.（22）当当ABCABC满足满足_条件时，四边形条件时，四边形DAEFDAEF是菱形是菱形.（33）当当ABCABC满足满足_条件时，条件时，以以DD、AA、EE、FF为顶点的四边形不存在为顶点的四边形不存在.如图:

三角形ABD,三角形ACE,三角形BCF都是等边三角形，首先我们来证明DAEF为平行四边形角DBF=60度-角FBA=角ABC而DB=AB,BF=BC三角形DBF全等于三角形ABC所以:

DF=AC=AE同理可证:

DA=FE所以:

DAEF为平行四边形

（1）如图,如果角DAE=90度,则DAEF为矩形则必须:

角BAC=360度-2*60度-90度=150度（而如果,另一种情况,BC为短边,F将落在DAECB的包围之中,角DAE=2*60度+角BAC90度,DAEF不可能为矩形,而BC为短边,角BAC90度）

（2）如果:

DA=AE,则:

DAEF为菱形，则必须:

AB=AC（3）如果:

角BAC=60度则:

角DAE=3*60度=180度D,A,E共线,所以:

以D、A、E、F为顶点的四边形不存在据此,

（2）的结论应稍加改变为:

当AB=AC,且角BAC不等于60度时,四边形DAEF是菱形6.已知已知:

如图如图,三角形三角形ABC中中,BAC=90度度,ADBC于点于点D,BE平分角平分角ABC交交AD于点于点M,EFBC于于F.求证求证:

四边形四边形AEFM是菱形是菱形.解答：

解答：

CE是角平分线，是角平分线，EACA，EFCF，CE=CE，CAECFE，EA=EF，AEC=FEC，又又ADCB，EFCB，ADEF，AGE=GEF，AEG=AGE，AG=AE，AG=EF，四边形四边形AGFE是平行四边形是平行四边形有一组对边平行且相等的四边形是平行四边形有一组对边平行且相等的四边形是平行四边形又又AG=AE，平行四边形平行四边形AGFE是菱形是菱形一组邻边相等的平行四边形是菱形一组邻边相等的平行四边形是菱形。

即：

四边形即：

四边形AEFG是菱形。

是菱形。

7.如图，在正方形如图，在正方形ABCD中，中，O为对角线为对角线AC和和BD的交点，的交点，E为为CO上一点，上一点，连接连接BE，F为为OBE角平分线上一点，连接角平分线上一点，连接OF、AF，G为为BE上一点且上一点且BO=BG。

（。

（1）若）若FGOF，OF=1,求线段求线段OG的长度；（的长度；

（2）若）若AFB90，求证：

，求证：

AFBF+OG

（1）、BF平分平分OBEOBF=GBFBO=BG，BF=BFOBFGBFOF=FGFGOFOFG是等腰直角三角形是等腰直角三角形OG=（OF+FG）=2

（2）、作、作OH垂直于垂直于OF交交AF于于HABCD是正方形，是正方形，BD、AC是对角线是对角线OA=OB，AOB=90HOF=90（做的做的OHOF）AOH=BOF（同为同为HOB的余角）的余角）AFB=AOB=90设设AF与与OB交于交于M，OMA=FMB（对顶角）对顶角）OAH（OAM）=OBF（MBF）在在AHO和和BOF中中OA=OB，AOH=BOF，OAH=OBFAHOBOFAH=BF，OH=OFOF=FG（第一步已经证明）第一步已经证明）OH=FGOFG=HOF=90（这一步有点问题，这一步有点问题，OFG在第一步是假设的，）在第一步是假设的，）OG=FHAF=AH+HF=BF+OG8.如图所示,在菱形ABCD中,对角线AC=6,BD=8,点E，F分别是边AB，BC的中点,点P在上运动，在运动过程中，存在PE+PF的最小值，则这个最小值为多少？

拓展：

若点在AC上运动，存在PE+PF的最小值，则这个最小值为多少？

解：

依题意得，当解：

依题意得，当P为为EF与与BD的交点时，的交点时，PE+PF最小，为最小，为EF的长的长.点点E、F分别为分别为AB、BC的中点，的中点，EF是是ABC的的中位线，中位线，EF=0.5AC=3.即即PE+PF的最小值为的最小值为3.拓展：

拓展：

用两张等宽的长方形纸条交叉重叠地放在一起用两张等宽的长方形纸条交叉重叠地放在一起,重合的部重合的部分为四边形分为四边形abcd，若长为，若长为8，宽为，宽为2，求四边形，求四边形abcd的最大的最大9.将俩张等宽的长方形纸条交叉叠放将俩张等宽的长方形纸条交叉叠放,重叠部分是一个四边形重叠部分是一个四边形ABCD,若若AD6，ABC60，则四边形，则四边形ABCD的面积是的面积是?

10.如图，已知菱形如图，已知菱形ABCD中，中，E,F分别是分别是BC,CD上的点，且上的点，且B=EAF=60，BAE=18，求，求CEF的度数的度数证明：

证明：

连接连接AC菱形菱形ABCD中，中，B=60AB=BC=CD=DA，AB=AC，FCA=B=60，又又EAF=60，CAF=BAE=18BAE全等于全等于CFA，AE=AFFEA=60，AEB=180-18-60=102CEF=180-FEA-AEB=180-60-102=1811.如图，如图，ABC中，中，BAC=90，BG平分平分ABC，GFBC于点于点F，ADBC于点于点D，交，交BG于点于点E，连结，连结EF。

（1）、求证：

）、求证：

、AE=AG；四边形四边形AEFG为菱形。

为菱形。

（2）、若）、若AD=8，BD=6，求，求AE的长。

的长。

证明证明:

（1）AE=AG的关键是证明的关键是证明AGE=AEG；AEG=BED，又，又ADB=90；AEG+GBD=90；又因为；又因为AGE+ABG=90且且BG为为角角ABD的角平分线，因此可以推断的角平分线，因此可以推断AEG=AGE，所以得出，所以得出AEG为等腰三角形，所以为等腰三角形，所以AE=AG。

（2）线段线段GF平行于线段平行于线段AD，所以，所以AEGFGE；AGB=FGB，有前面的条件可知，有前面的条件可知ABG=角角FBG，又，又BG=BG，所以三角形，所以三角形ABG全等于三角形全等于三角形GFB，所以，所以AG=AF，从而推出，从而推出AE=GF，根据菱形的定义：

四边形，根据菱形的定义：

四边形AEFG为平行为平行四边形，又邻边相等，所以四边形为菱形。

四边形，又邻边相等，所以四边形为菱形。

（3）AD=8,BD=6,AB=BF=8,DE/GF,BD/BF=DE/FG.设AE=x，则ED=8-x,GF=X,即：

6/10=（8-x）/x.解得x=8/3.ABCDEFG

（1）解：

连接BD,点E为CD边的中点,BECDBD=BCDBE=CBEFBE=2EBCDBE=CBE=DBFBF=BGFBDGBC13.如图，在矩形如图，在矩形ABCD中。

已知中。

已知AD=12,AB=5，P是是AD上任上任意一点，意一点，PEBD，PFAC，E和和F分别是垂足，求分别是垂足，求PE+PF的的值值.ABDCPFE提示：

用三角