 单方程第5题ARIMA模型例59建立中国GDP对数序列的ARIMA模型文档格式.docx
单方程第5题ARIMA模型例59建立中国GDP对数序列的ARIMA模型文档格式.docx
- 文档编号:17535330
- 上传时间:2022-12-07
- 格式:DOCX
- 页数:25
- 大小:230.35KB
单方程第5题ARIMA模型例59建立中国GDP对数序列的ARIMA模型文档格式.docx
《单方程第5题ARIMA模型例59建立中国GDP对数序列的ARIMA模型文档格式.docx》由会员分享,可在线阅读,更多相关《单方程第5题ARIMA模型例59建立中国GDP对数序列的ARIMA模型文档格式.docx(25页珍藏版)》请在冰豆网上搜索。
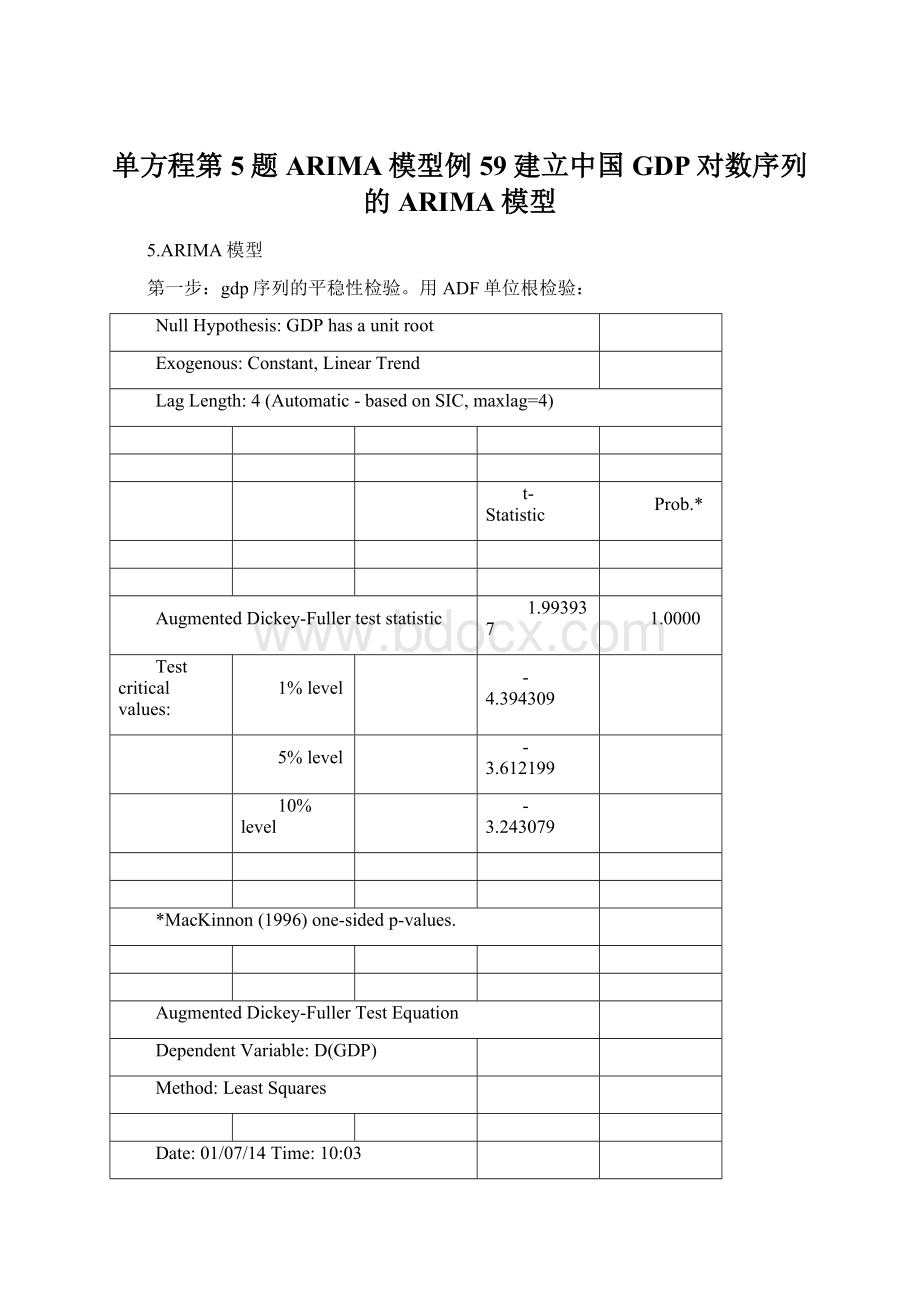
10%level
-3.243079
*MacKinnon(1996)one-sidedp-values.
AugmentedDickey-FullerTestEquation
DependentVariable:
D(GDP)
Method:
LeastSquares
Date:
01/07/14Time:
10:
03
Sample(adjusted):
19832006
Includedobservations:
24afteradjustments
Variable
Coefficient
Std.Error
Prob.
GDP(-1)
0.069206
0.034708
0.0625
D(GDP(-1))
1.078825
0.239934
4.496342
0.0003
D(GDP(-2))
-0.860946
0.406194
-2.119545
0.0491
D(GDP(-3))
0.728386
0.501847
1.451411
0.1649
D(GDP(-4))
-0.813788
0.350036
-2.324869
0.0327
C
-402.4700
1591.446
-0.252896
0.8034
@TREND(1980)
161.2485
214.6915
0.751071
0.4629
R-squared
0.944348
Meandependentvar
8564.483
AdjustedR-squared
0.924706
S.D.dependentvar
7687.518
S.E.ofregression
2109.437
Akaikeinfocriterion
18.38472
Sumsquaredresid
75645293
Schwarzcriterion
18.72832
Loglikelihood
-213.6167
Hannan-Quinncriter.
18.47588
F-statistic
48.07816
Durbin-Watsonstat
2.069518
Prob(F-statistic)
0.000000
gdp序列以最大的p值,即100%的显著性接受原假设,即存在单位根。
第二步检验gdp一阶差分的平稳性,结果如下:
在16.66%的显著性水平下接受原假设,存在单位根,序列非平稳
第三步:
检验gdp二阶差分的平稳性,选择无常数项,趋势项,滞后阶数为0,结果如下:
D2GDPhasaunitroot
Constant
0(Automatic-basedonSIC,maxlag=0)
-3.291626
0.0258
-3.711457
-2.981038
-2.629906
D(D2GDP)
15
19812006
26afteradjustments
D2GDP(-1)
-0.633042
0.192319
0.0031
687.3110
496.7749
1.383546
0.1792
0.311034
113.3808
0.282327
2799.855
2371.914
18.45459
1.35E+08
18.55136
-237.9096
18.48245
10.83480
1.868580
0.003074
T统计值小于相关临界值故认为是没有单位根的,由上述结果可见gdp序列是二阶单整序列
第四步检验ln(gdp)稳定性
LNGDPhasaunitroot
4(Automatic-basedonSIC,maxlag=6)
-1.055147
0.7160
-3.737853
-2.991878
-2.635542
D(LNGDP)
22
LNGDP(-1)
-0.008351
0.007914
0.3053
D(LNGDP(-1))
1.016055
0.210339
4.830562
0.0001
D(LNGDP(-2))
-0.738330
0.292511
-2.524109
0.0212
D(LNGDP(-3))
0.533862
0.293618
1.818219
0.0857
D(LNGDP(-4))
-0.411638
0.202529
-2.032488
0.0571
0.178697
0.089949
1.986645
0.0624
0.669413
0.153297
0.577584
0.064378
0.041842
-3.297535
0.031513
-3.003021
45.57042
-3.219400
7.289734
1.834540
0.000685
有上述结果认为lngdp是非平稳序列
第五步检验lngdp一阶差分平稳性,结果如下:
DLNGDPhasaunitroot
1(Automatic-basedonSIC,maxlag=1)
-2.999109
0.0482
D(DLNGDP)
26
DLNGDP(-1)
-0.442908
0.147680
0.0064
D(DLNGDP(-1))
0.420961
0.187574
2.244240
0.0347
0.065385
0.023268
2.810145
0.0099
0.311077
0.000950
0.251171
0.051436
0.044510
-3.278037
0.045566
-3.132872
45.61448
-3.236235
5.192728
1.852831
0.013771
由上述结果,认为lngdp的一阶差分是平稳的,lngdp一阶差分序列相关图如下。
6.ARIMA模型
Sample
- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 方程 ARIMA 模型 59 建立 中国 GDP 对数 序列
 冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
冰豆网所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。


 如何打造酒店企业文化2刘田江doc.docx
如何打造酒店企业文化2刘田江doc.docx
