简单的逻辑联结词全称量词与存在量词教案重点Word文档下载推荐.docx

简单的逻辑联结词全称量词与存在量词教案重点Word文档下载推荐.docx

《简单的逻辑联结词全称量词与存在量词教案重点Word文档下载推荐.docx》由会员分享，可在线阅读，更多相关《简单的逻辑联结词全称量词与存在量词教案重点Word文档下载推荐.docx（11页珍藏版）》请在冰豆网上搜索。

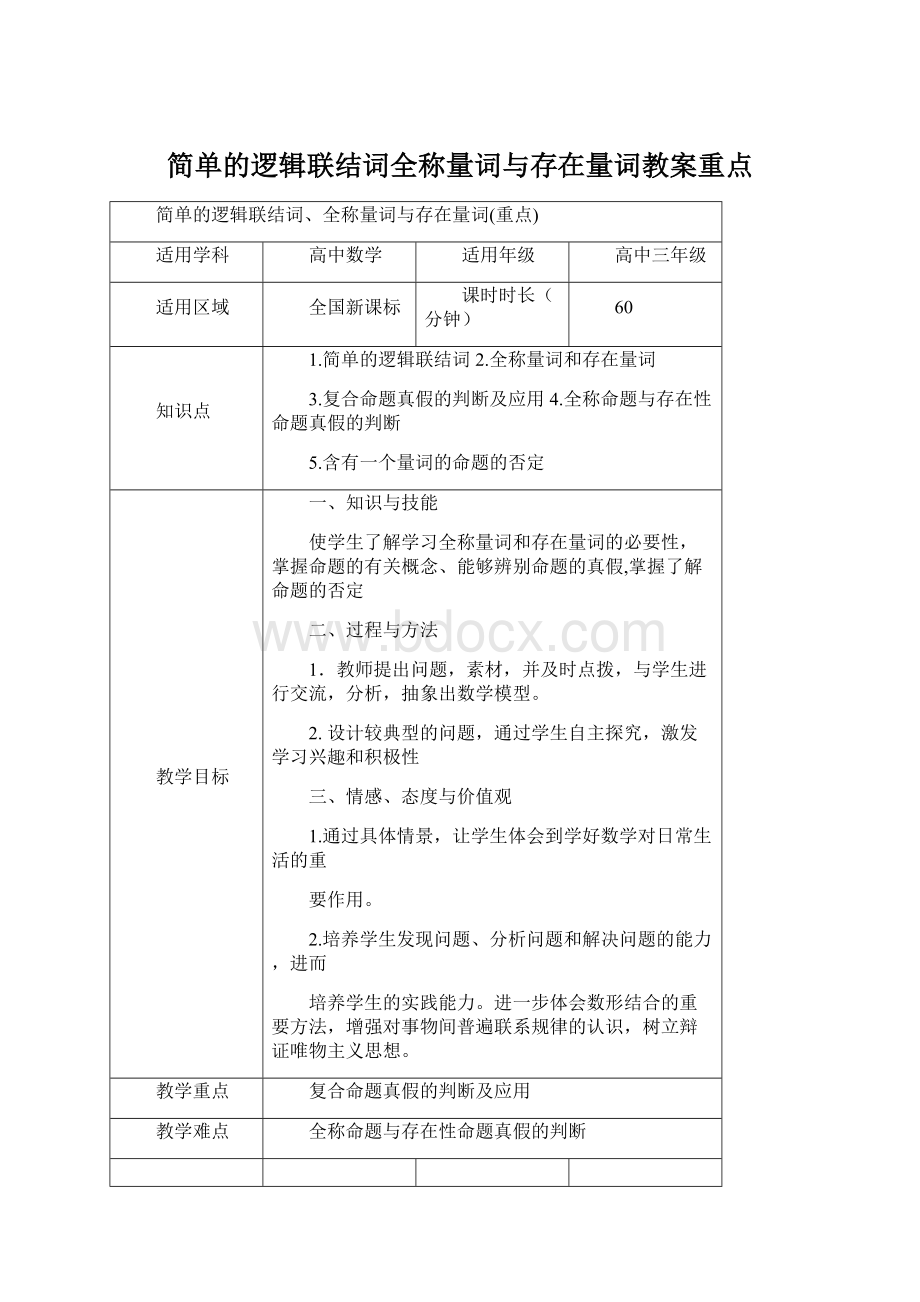
教学重点

复合命题真假的判断及应用

教学难点

全称命题与存在性命题真假的判断

教学过程

一.课程导入：

在大量的数学实例的基础上，思考、探究、分析、发现，最后总结概括出相关概念和知识，是本章容的突出特色。

本章容，重在让学生通过对常用逻辑用语的学习，体会运用逻辑用语在表述和论证中的作用，能用这些逻辑用语准确地表达数学容，更好地进行交流。

为此，教科书在安排容时，就突出了让学生领会这些常用逻辑用语的含义，从而更好的运用这些常用逻辑用语的这一目的。

本章容与学生日常生活中的某些概念有一定关联，但就在数学上的运用和含义还有一定差别，因此数学中如何正确理解和运用这些常用逻辑用语，是本章的关键也是较难处理的，为此，教科书是从大量的丰富数学实例出发，来帮助学生认识数学中的这些常用逻辑用语的含义的。

例如，对“命题”概念的阐述，就是通过总结6个数学例子的基础上概括得出的；

对于四种命题及其关系，也是通过对命题“若f（x）是正弦函数，则f（x）是周期函数”的条件与结论的互换及否定等具体例子的讨论，达到对四种命题及其关系的认识；

逻辑联结词“或”“且”“非”含义和用法的介绍，也是通过学生熟悉的数学实例讲授的；

学习完命题及命题的否定后，教科书又安排了丰富的实例，使学生了解生活和数学中经常使用的两类量词（全称量词和存在量词），并通过例子说明如何对含有一个量词的命题进行正确地否定。

二、复习预习

复习时应紧扣概念，理清相似概念间的异同点，准确把握逻辑联结词的含义和用法，熟练掌握对含有量词命题的否定的方法．本讲常与其他知识结合，在知识的交汇处命题，试题难度中档偏下．　　

三、知识讲解

考点1、简单的逻辑联结词

（1）命题中的“且”“或”“非”叫做逻辑联结词．

（2）简单复合命题的真值表：

p

q

p∧q

p∨q

¬

真

假

考点2、全称量词与存在量词

（1）常见的全称量词有：

“任意一个”“一切”“每一个”“任给”“所有的”等．

（2）常见的存在量词有：

“存在一个”“至少有一个”“有些”“有一个”“某个”“有的”等．

（3）全称量词用符号“∀”表示；

存在量词用符号“∃”表示．

考点3、全称命题与特称命题

（1）含有全称量词的命题叫全称命题．

（2）含有存在量词的命题叫特称命题．

考点4、命题的否定

（1）全称命题的否定是特称命题；

特称命题的否定是全称命题．

（2）p或q的否定为：

非p且非q；

p且q的否定为：

非p或非q.

四、例题精析

【例题1】

【题干】已知命题p1：

函数y＝2x－2－x在R上为增函数，p2：

函数y＝2x＋2－x在R上为减函数，则在命题q1：

p1∨p2，q2：

p1∧p2，q3：

（¬

p1）∨p2和q4：

p1∧（¬

p2）中，真命题是（　　）．

A．q1，q3B．q2，q3

C．q1，q4D．q2，q4

【答案】C

【解析】可判断p1为真，p2为假；

则q1为真，q2为假，q3为假，q4为真．

【例题2】

【题干】已知命题p：

∃x0∈R，使sinx0＝

；

命题q：

∀x∈R，都有x2＋x＋1＞0.给出下列结论

①命题“p∧q”是真命题；

②命题“¬

p∨¬

q”是假命题；

③命题“¬

p∨q”是真命题；

④命题“p∨¬

q”是假命题．

其中正确的是（　　）．

A．②③B．②④

C．③④D．①②③

【解析】命题p是假命题，命题q是真命题，故③④正确．

【例题3】

【题干】写出下列命题的否定，并判断其真假．

（1）p：

∀x∈R，x2－x＋

≥0；

（2）q：

所有的形都是矩形；

（3）r：

∃x0∈R，x

＋2x0＋2≤0；

（4）s：

至少有一个实数x0，使x

＋1＝0.

【答案】见解析

【解析】

（1）¬

p：

－x0＋

＜0，假命题．

（2）¬

q：

至少存在一个形不是矩形，假命题．

（3）綈r：

∀x∈R，x2＋2x＋2＞0，真命题．

（4）綈s：

∀x∈R，x3＋1≠0，假命题．

【例题4】

【题干】写出下列命题的否定，并判断真假．

∀x∈R，x不是3x－5＝0的根；

有些合数是偶数；

∃x0∈R，|x0－1|＞0.

∃x0∈R，x0是3x－5＝0的根，真命题．

每一个合数都不是偶数，假命题．

∀x∈R，|x－1|≤0，假命题．

五、课堂运用

【基础】

1.已知命题p：

∀x∈R，sinx≤1，则（　　）．　　　　　　　

A．¬

∃x0∈R，sinx0≥1B．¬

∀x∈R，sinx≥1

C．¬

∃x0∈R，sinx0>

1D．¬

∀x∈R，sinx>

1

【解析】命题p是全称命题，全称命题的否定是特称命题．

2.若p是真命题，q是假命题，则（　　）．

A．p∧q是真命题B．p∨q是假命题

p是真命题D．¬

q是真命题

【答案】D

【解析】本题考查命题和逻辑联结词的基础知识，意在考查考生对逻辑联结词的理解运用能力．只有¬

q是真命题．

3.命题p：

若a，b∈R，则|a|＋|b|＞1是|a＋b|＞1的充分而不必要条件．命题q：

函数y＝

的定义域是（－∞，－1]∪[3，＋∞）则（　　）．

A．“p或q”为假B．“p且q”为真

C．p真q假D．p假q真

【答案】D

【解析】根据定义

4.设p、q是两个命题，则复合命题“p∨q为真，p∧q为假”的充要条件是

（　　）．

A．p、q中至少有一个为真B．p、q中至少有一个为假

C．p、q中有且只有一个为真D．p为真、q为假

【解析】略

【巩固】

5.命题“对任何x∈R，|x－2|＋|x－4|>

3”的否定是______________________．

【解析】存在x0∈R，使|x0－2|＋|x0－4|≤3　　

6.已知命题p：

方程x2＋mx＋1＝0有两个不等的负实数根；

方程4x2＋4（m－2）x＋1＝0无实数根．若“p或q”为真命题，“p且q”为假命题，求m的取值围．

【解析】　由p得：

则m＞2.

由q得：

Δ2＝16（m－2）2－16＝16（m2－4m＋3）＜0，

则1＜m＜3.

又∵“p或q”为真，“p且q”为假，∴p与q一真一假．

①当p真q假时，

解得m≥3；

②当p假q真时，

解得1＜m≤2.

∴m的取值围为m≥3或1＜m≤2.

7.已知a＞0，设命题p：

函数y＝ax在R上单调递增；

不等式ax2－ax＋1＞0对∀x∈R恒成立．若p且q为假，p或q为真，求a的取值围．

【解析】∵函数y＝ax在R上单调递增，∴p：

a＞1.

不等式ax2－ax＋1＞0对∀x∈R恒成立，

∴a＞0且a2－4a＜0，解得0＜a＜4，∴q：

0＜a＜4.

∵“p∧q”为假，“p∨q”为真，

∴p、q中必有一真一假．

得a≥4.

得0＜a≤1.

故a的取值围为（0,1]∪[4，＋∞）．　　

【拔高】

8.已知c＞0，且c≠1，设p：

函数y＝cx在R上单调递减；

函数f（x）＝x2－2cx＋1在

上为增函数，若“p∧q”为假，“p∨q”为真，数c的取值围．

【解析】　∵函数y＝cx在R上单调递减，

∴0＜c＜1.（2分）

即p：

0＜c＜1.∵c＞0且c≠1，∴¬

c＞1.（3分）

又∵f（x）＝x2－2cx＋1在

上为增函数，

∴c≤

.即q：

0＜c≤

.

∵c＞0且c≠1，∴¬

c＞

且c≠1.（6分）

又∵“p∨q”为真，“p∧q”为假，∴p真q假或p假q真．（7分）

①当p真，q假时，{c|0＜c＜1}∩

＝

（9分）

②当p假，q真时，{c|c＞1}∩

＝∅.（11分）

综上所述，实数c的取值围是

.（12分）

9.设p：

方程x2＋2mx＋1＝0有两个不相等的正根；

方程x2＋2（m－2）x－3m＋10＝0无实根．求使p∨q为真，p∧q为假的实数m的取值围．

【解析】由

得m＜－1.

∴p：

m＜－1；

由Δ2＝4（m－2）2－4（－3m＋10）＜0，

知－2＜m＜3，∴q：

－2＜m＜3.

由p∨q为真，p∧q为假可知，命题p，q一真一假，

当p真q假时，

此时m≤－2；

当p假q真时，

此时－1≤m＜3.

∴m的取值围是{m|m≤－2，或－1≤m＜3}．

六、课堂小结

一个关系

逻辑联结词与集合的关系

“或、且、非”三个逻辑联结词，对应着集合运算中的“并、交、补”，因此，常常借助集合的“并、交、补”的意义来解答由“或、且、非”三个联结词构成的命题问题．

两类否定

1．含有一个量词的命题的否定

（1）全称命题的否定是特称命题

全称命题p：

∀x∈M，p（x），它的否定¬

∃x0∈M，¬

p（x0）．

（2）特称命题的否定是全称命题

特称命题p：

∃x0∈M，p（x0），它的否定¬

∀x∈M，¬

p（x）．

2．复合命题的否定

（1）綈（p∧q）⇔（¬

p）∨（¬

q）；

（2）綈（p∨q）⇔（¬

p）∧（¬

q）．

三条规律

（1）对于“p∧q”命题：

一假则假；

（2）对“p∨q”命题：

一真则真；

（3）对“¬

p”命题：

与“p”命题真假相反．