春苏科版七年级数学下册72探索平行线的性质 平行线的性质自主学习同步训练1附答案Word文件下载.docx

春苏科版七年级数学下册72探索平行线的性质 平行线的性质自主学习同步训练1附答案Word文件下载.docx

《春苏科版七年级数学下册72探索平行线的性质 平行线的性质自主学习同步训练1附答案Word文件下载.docx》由会员分享，可在线阅读，更多相关《春苏科版七年级数学下册72探索平行线的性质 平行线的性质自主学习同步训练1附答案Word文件下载.docx（19页珍藏版）》请在冰豆网上搜索。

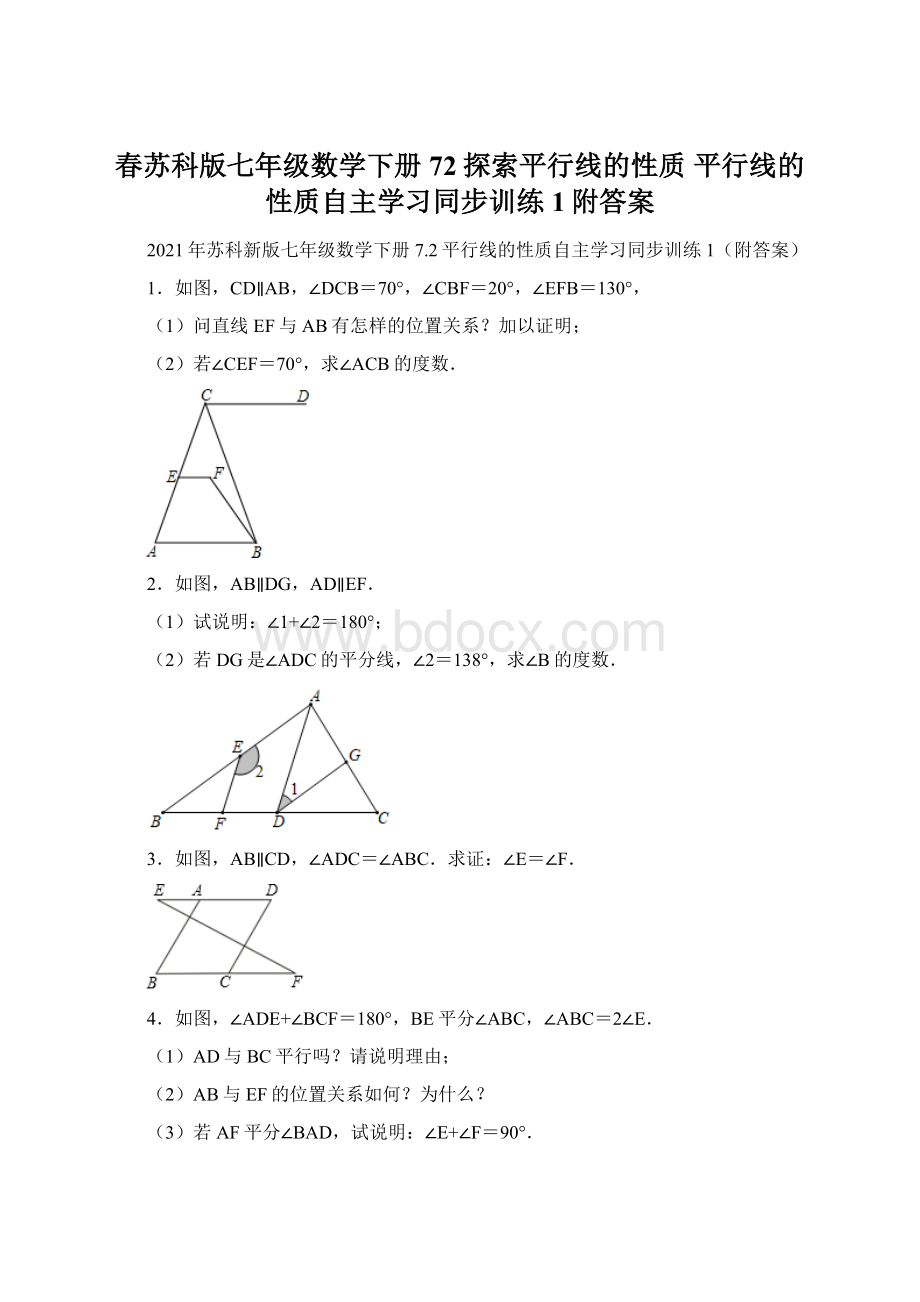
，DF平分∠ADE，求∠B的度数．

9．如图，AB∥CD，AE平分∠BAD，CD与AE相交于F，∠CFE＝∠E．求证：

AD∥BC．

10．将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

CF∥AB；

（2）求∠DFC的度数．

11．如图所示，点B，E分别在AC，DF上，BD，CE均与AF相交，∠1＝∠2，∠C＝∠D，求证：

∠A＝∠F．

12．已知：

如图，AE⊥BC，FG⊥BC，∠1＝∠2

AB∥CD

（2）若∠D＝∠3+50°

，∠CBD＝70°

，求∠C的度数．

13．如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F，∠1＝∠2．

（1）试说明DG∥BC的理由；

（2）如果∠B＝54°

，且∠ACD＝35°

，求∠3的度数．

14．如图，直线a∥b，射线DF与直线a相交于点C，过点D作DE⊥b于点E，已知∠1＝25°

，求∠2的度数．

15．如图，AP，CP分别平分∠BAC，∠ACD，∠P＝90°

，设∠BAP＝α．

（1）用α表示∠ACP；

（2）求证：

AB∥CD；

（3）若AP∥CF，求证：

FC平分∠DCE．

16．如图，AE∥CF，∠A＝∠C．

（1）若∠1＝35°

，求∠2的度数；

（2）判断AD与BC的位置关系，并说明理由；

（3）若AD平分∠BDF，试说明BC平分∠DBE．

17．已知AD∥BC，AB∥CD，E为射线BC上一点，AE平分∠BAD．

（1）如图1，当点E在线段BC上时，求证：

∠BAE＝∠BEA．

（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE＝3∠CDE，∠AED＝60°

①求证：

∠ABC＝∠ADC；

②求∠CED的度数．

18．如图，已知BC∥GE，AF∥DE，∠1＝50°

（1）求∠AFG的度数；

（2）若AQ平分∠FAC，交BC于点Q，且∠Q＝15°

19．如图，已知射线AB与直线CD交于点O，OF平分∠BOC，OG⊥OF于O，AE∥OF，且∠A＝30°

（1）求∠DOF的度数；

（2）试说明OD平分∠AOG．

20．已知：

如图，C，D是直线AB上两点，∠1+∠2＝180°

，DE平分∠CDF，EF∥AB，

CE∥DF；

（2）若∠DCE＝130°

，求∠DEF的度数．

21．如图，AB∥CD，∠1＝∠2，∠3＝∠4，试说明AD∥BE．

22．已知如图，DE⊥AC，∠AGF＝∠ABC，∠1+∠2＝180°

，试判断BF与AC的位置关系，并说明理由．

23．如图：

已知AB∥DE∥CF，若∠ABC＝70°

，∠CDE＝130°

，求∠BCD的度数．

24．如图，已知CF⊥AB于F，ED⊥AB于D，∠1＝∠2，求证：

FG∥BC．

25．如图，CD平分∠ACB，DE∥BC，∠AED＝80°

，求∠EDC的度数．

参考答案

1．解：

（1）EF和AB的关系为平行关系．理由如下：

∵CD∥AB，∠DCB＝70°

∴∠DCB＝∠ABC＝70°

∵∠CBF＝20°

∴∠ABF＝∠ABC﹣∠CBF＝50°

∵∠EFB＝130°

∴∠ABF+∠EFB＝50°

+130°

＝180°

∴EF∥AB；

（2）∵EF∥AB，CD∥AB，

∴EF∥CD，

∵∠CEF＝70°

∴∠ECD＝110°

∵∠DCB＝70°

∴∠ACB＝∠ECD﹣∠DCB，

∴∠ACB＝40°

2．解：

（1）∵AD∥EF，

∴∠BAD+∠2＝180°

∵AB∥DG，

∴∠BAD＝∠1，

∴∠1+∠2＝180°

（2）∵∠1+∠2＝180°

且∠2＝138°

∴∠1＝42°

∵DG是∠ADC的平分线，

∴∠CDG＝∠1＝42°

∴∠B＝∠CDG＝42°

3．证明：

∵AB∥CD，

∴∠ABC＝∠DCF．

又∵∠ADC＝∠ABC

∴∠ADC＝∠DCF．

∴DE∥BF．

∴∠E＝∠F．

4．解：

（1）AD∥BC，

理由是：

∵∠ADE+∠BCF＝180°

，∠ADE+∠ADF＝180°

∴∠ADF＝∠BCF，

∴AD∥BC；

（2）AB∥EF，

∵BE平分∠ABC，

∴∠ABC＝2∠ABE，

∵∠ABC＝2∠E，

∴∠ABE＝∠E，

∴AB∥EF；

（3）∵AD∥BC，

∴∠DAB+∠ABC＝180°

∵BE平分∠ABC，AF平分∠BAD，

∴∠ABE＝

ABC，∠BAF＝

∠BAD，

∴∠ABE+∠BAF＝90°

∴∠AOB＝180°

﹣90°

＝90°

＝∠EOF，

∴∠E+∠F＝180°

﹣∠EOF＝90°

5．解：

（1）∵∠CED＝∠GHD，

∴CE∥GF；

（2）∠AED+∠D＝180°

理由：

∵CE∥GF，

∴∠C＝∠FGD，

又∵∠C＝∠EFG，

∴∠FGD＝∠EFG，

∴AB∥CD，

∴∠AED+∠D＝180°

（3）∵∠GHD＝∠EHF＝80°

∴∠CGF＝80°

+30°

＝110°

又∵CE∥GF，

∴∠C＝180°

﹣110°

＝70°

又∵AB∥CD，

∴∠AEC＝∠C＝70°

∴∠AEM＝180°

﹣70°

6．证明：

∵∠ABC+∠ECB＝180°

∴AB∥DE，

∴∠ABC＝∠BCD，

∵∠P＝∠Q，

∴PB∥CQ，

∴∠PBC＝∠BCQ，

∵∠1＝∠ABC﹣∠PBC，∠2＝∠BCD﹣∠BCQ，

∴∠1＝∠2．

7．解：

（1）AC∥DF，理由如下：

∵∠1＝80°

∴BD∥CE，

∴∠ABD＝∠C，

∵∠C＝∠D，

∴∠ABD＝∠D，

∴AC∥DF；

（2）∵AC∥DF，

∴∠A＝∠F，∠ABD＝∠D，

∵∠C＝∠D，∠1＝80°

∴∠A+∠ABD＝180°

﹣80°

＝100°

即∠A+∠C＝100°

∵∠C比∠A大20°

∴∠A＝40°

∴∠F＝40°

8．解：

（1）∵AC∥DE，

∴∠C＝∠1，

∵∠AFD＝∠1，

∴∠C＝∠AFD，

∴DF∥BC．

（2）∵∠1＝68°

，DF∥BC，

∴∠EDF＝∠1＝68°

∵DF平分∠ADE，

∴∠ADF＝∠EDF＝68°

∵DF∥BC，

∴∠B＝∠ADF＝68°

9．证明：

∵AE平分∠BAD，

∴∠1＝∠2，

∵AB∥CD，∠CFE＝∠E，

∴∠1＝∠CFE＝∠E，

∴∠2＝∠E，

∴AD∥BC．

10．

（1）证明：

由题意知，△ACB是等腰直角三角形，且∠ACB＝∠DCB＝90°

∴∠B＝45°

∵CF平分∠DCE，

∴∠DCF＝∠ECF＝45°

∴∠B＝∠ECF，

∴CF∥AB．

（2）由三角板知，∠E＝60°

由

（1）知，∠ECF＝45°

∵∠DFC＝∠ECF+∠E，

∴∠DFC＝45°

+60°

＝105°

11．证明：

∵∠2＝∠3，∠1＝∠2，

∴∠1＝∠3，

∴∠C＝∠ABD；

又∵∠C＝∠D，

∴∠D＝∠ABD，

∴AB∥EF，

∴∠A＝∠F．

12．

（1）证明：

∵AE⊥BC，FG⊥BC，

∴∠AMB＝∠GNM＝90°

∴AE∥FG，

∴∠A＝∠2；

又∵∠2＝∠1，

∴∠A＝∠1，

∴AB∥CD；

（2）解：

∴∠D+∠CBD+∠3＝180°

∵∠D＝∠3+50°

∴∠3＝30°

∴∠C＝∠3＝30°

13．

（1）证明：

∵CD⊥AB，EF⊥AB，

∴CD∥EF，

∴∠2＝∠BCD．

又∵∠1＝∠2，

∴∠1＝∠BCD，

∴DG∥BC．

在Rt△BEF中，∠B＝54°

∴∠2＝180°

﹣54°

＝36°

∴∠BCD＝∠2＝36°

又∵BC∥DG，

∴∠3＝∠ACB＝∠ACD+∠BCD＝35°

+36°

＝71°

14．解：

过点D作DG∥b，

∵a∥b，且DE⊥b，

∴DG∥a，

∴∠1＝∠CDG＝25°

，∠GDE＝∠3＝90°

∴∠2＝∠CDG+∠GDE＝25°

+90°

＝115°

15．

（1）解：

∵AP平分∠BAC，

∴∠CAP＝∠BAP＝α，

∵∠P＝90°

∴∠ACP＝90°

﹣∠CAP＝90°

﹣α；

（2）证明：

由

（1）可知∠ACP＝90°

﹣α，

∵CP平分∠ACD，

∴∠ACD＝2∠ACP＝180°

﹣2α，

又∠BAC＝2∠BAP＝2α，

∴∠ACD+∠BAC＝180°

（3）证明：

∵AP∥CF，

∴∠ECF＝∠CAP＝α，

由

（2）可知AB∥CD，

∴∠ECD＝∠CAB＝2α，

∴∠DCF＝∠ECD﹣∠ECF＝α，

∴∠ECF＝∠DCF，

∴CF平分∠DCE．

16．解：

（1）∵AE∥CF，

∴∠BDC＝∠1＝35°

又∵∠2+∠BDC＝180°

﹣∠BDC＝180°

﹣35°

＝145°

（2）BC∥AD．

∵AE∥CF，

∴∠A+∠ADC＝180°

又∵∠A＝∠C，

∴∠C+∠ADC＝180°

∴BC∥AD．

（3）∵AE∥CF，

∴∠BDF＝∠DBE．

∵BC∥AD，

∴∠ADB＝∠DBC．

∵AD平分∠BDF，

∴∠ADB＝

∠BDF，

∴∠DBC＝

∠EBD．

∴BC平分∠DBE．

17．

（1）证明：

∴∠BAE＝∠EAD，

∵AD∥BC，

∴∠AEB＝∠EAD，

∴∠BAE＝∠BEA；

（2）①证明：

∵AD∥BC，AB∥CD，

∴四边形ABCD是平行四边形，

∴∠ABC＝∠ADC；

②解：

∵∠ADE＝3∠CDE，设∠CDE＝x°

∴∠ADE＝3x°

，∠ADC＝2x°

∴∠BAD+∠ADC＝180°

∴∠DAB＝180°

﹣2x°

∵∠DAE＝∠BAE＝∠BEA＝90°

﹣x°

又∵AD∥BC，

∴∠BED+∠ADE＝180°

∵∠AED＝60°

即90﹣x+60+3x＝180，

∴∠CDE＝x°

＝15°

，∠ADE＝45°

∴∠CED＝180°

﹣∠ADE＝135°

18．解：

（1）∵BC∥EG，

∴∠E＝∠1＝50°

∵AF∥DE，

∴∠AFG＝∠E＝50°

（2）作AM∥BC，

∵BC∥EG，

∴AM∥EG，

∴∠FAM＝∠AFG＝50°

∵AM∥BC，

∴∠QAM＝∠Q＝15°

∴∠FAQ＝∠FAM+∠QAM＝65°

∵AQ平分∠FAC，

∴∠QAC＝∠FAQ＝65°

∴∠MAC＝∠QAC+∠QAM＝80°

∴∠ACB＝∠MAC＝80°

19．解：

（1）∵AE∥OF，

∴∠FOB＝∠A＝30°

∵OF平分∠BOC，

∴∠COF＝∠FOB＝30°

∴∠DOF＝180°

﹣∠COF＝150°

（2）∵OF⊥OG，

∴∠FOG＝90°

∴∠DOG＝∠DOF﹣∠FOG＝150°

＝60°

∵∠AOD＝∠COB＝∠COF+∠FOB＝60°

∴∠AOD＝∠DOG，

∴OD平分∠AOG．

20．

（1）证明：

∵∠1+∠2＝180°

，C，D是直线AB上两点，

∴∠1+∠DCE＝180°

∴∠2＝∠DCE，

∴CE∥DF；

∵CE∥DF，∠DCE＝130°

∴∠CDF＝180°

﹣∠DCE＝180°

﹣130°

＝50°

∵DE平分∠CDF，

∴∠CDE＝

∠CDF＝25°

∵EF∥AB，

∴∠DEF＝∠CDE＝25°

21．证明：

∴∠1＝∠6，

∵∠1＝∠2，∠3＝∠4，

∴∠3+∠6＝∠4+∠2，

∵∠4＝∠5，

∴∠3+∠6＝∠2+∠5，

∵∠2+∠5+∠D＝180°

∴∠3+∠6+∠D＝180°

即∠BCD+∠D＝180°

∴AD∥BE．

22．解：

BF与AC的位置关系是：

BF⊥AC．

∵∠AGF＝∠ABC，

∴BC∥GF（同位角相等，两直线平行），

又∵∠1+∠2＝180°

∴∠2+∠3＝180°

∴BF∥DE，

∵DE⊥AC，

∴BF⊥AC．

23．解：

∵AB∥CF，∠ABC＝70°

∴∠BCF＝∠ABC＝70°

又∵DE∥CF，∠CDE＝130°

∴∠DCF+∠CDE＝180°

∴∠DCF＝50°

∴∠BCD＝∠BCF﹣∠DCF＝70°

﹣50°

＝20°

24．证明：

∵CF⊥AB，ED⊥AB，

∴DE∥FC（垂直于同一条直线的两条直线互相平行），

∴∠1＝∠BCF（两直线平行，同位角相等）；

又∵∠2＝∠1（已知），

∴∠BCF＝∠2（等量代换），

∴FG∥BC（内错角相等，两直线平行）．

25．解：

∵DE∥BC，∠AED＝80°

∴∠ACB＝∠AED＝80°

（两直线平行，同位角相等），

∵CD平分∠ACB，

∴∠BCD＝

∠ACB＝40°

∵DE∥BC，

∴∠EDC＝∠BCD＝40°

（两直线平行，内错角相等）